# A tibble: 5,384 × 17
ID date Team Opponent Goal tournament Home form diff_point diff_rank days_since_last city country rank total_points previous_points rank_date
<int> <date> <chr> <chr> <int> <chr> <dbl> <dbl> <int> <int> <dbl> <chr> <chr> <int> <int> <int> <date>
1 1 2010-03-03 Albania Northern Ireland 1 Friendly 1 5.39 -413 -57 109 Tirana Albania 96 335 336 2010-03-03
2 1 2010-03-03 Northern Ireland Albania 0 Friendly 0 2.09 413 57 109 Tirana Albania 39 748 729 2010-03-03
3 2 2010-03-03 Armenia Belarus 1 Friendly 0 9.22 -80 -24 140 Antalya Turkey 103 320 321 2010-03-03
4 2 2010-03-03 Belarus Armenia 3 Friendly 0 4.29 80 24 105 Antalya Turkey 79 400 397 2010-03-03
5 3 2010-03-03 Austria Denmark 2 Friendly 1 6.37 -231 -23 105 Vienna Austria 56 567 523 2010-03-03
6 3 2010-03-03 Denmark Austria 1 Friendly 0 6.84 231 23 140 Vienna Austria 33 798 827 2010-03-03
7 4 2010-03-03 Belgium Croatia 0 Friendly 1 15.3 -559 -57 109 Brussels Belgium 68 491 491 2010-03-03
8 4 2010-03-03 Croatia Belgium 1 Friendly 0 6.88 559 57 109 Brussels Belgium 11 1050 1053 2010-03-03
9 5 2010-03-03 Cyprus Iceland 0 Friendly 1 10.9 140 25 140 Larnaca Cyprus 66 495 471 2010-03-03
10 5 2010-03-03 Iceland Cyprus 0 Friendly 0 10.1 -140 -25 109 Larnaca Cyprus 91 355 349 2010-03-03
# … with 5,374 more rowsEuros prediction
I wasn’t going to do much about this (and probably, I shouldn’t have done anything and used my time more wisely…), but a couple of friends/colleagues have actually asked me if I had done it and Italy did so well in their first outing, that I was up last night to whip something up… (in case it’s not clear yet, yes: this is a post on using Bayesian modelling to predict the outcome of football games, specifically for the ongoing Euro championships).
So: it’s actually very fortunate that lots of the relevant data are fairly easy to get. Kaggle have a dataset including all international games from 1972 to 2021 (before the Euros began last week). They also have a dataset with the FIFA ranking for each of the national teams. And the games schedule is also available from a simple Google search.
These three datasets can be combined to create the actual data to analyse and use for prediction of the Euro championship games. In particular, I have constructed a “long” format data where each game is replicated twice and the two rows are from the “point of view” of each opponent — like below. I have filtered only the data from 2010 onward.
In this table, ID is equal to 1 in the first two rows, to indicate that the first game is played between Albania and Northern Ireland. In the game, Albania scored 1, while Northern Ireland scored 0. The game was a Friendly match and because it was played in Tirana, Albania, the variable Home is set to 1 for Albania and 0 for their opponents. Also, using the FIFA ranking data, I’ve calculated the actual rank and total points at the time of the game and then reconstructed the difference in points and ranks between the two teams (respectively in the variables diff_point and diff_rank).
I’ve also computed the number of days since the last game was played by either teams involved (stored in the variable days_since_last). I’m using this in combination with another derived variable, form, which I have computed to give an indication of how good a run a team are having. In particular, form is defined as the weighted sum of the points accrued in the last 3 games, where the weights are computed as a function of the difference in “strength” (according to the total FIFA points each team had, going into the game). So, for each game I compute the proportion of points over the total for the two teams and use its inverse to weigh the number of points actually won in the game (3 for a win, 1 for a draw and 0 for a loss); this is meant to imply that if you beat a team that is way worse than you, that should count for much less than when you’re a crappy team and beat the World Champions…
With data formatted in this way, I’m ready to run a model that is based on a relatively standard format (and the specific Bayesian version we implemented here). The model assumes that the number of goals scored in each game is \(y_{g}\) in game \(g=1,\ldots,G\) (because of the long format in which I’ve constructed the dataset, this is the same as assuming two variables, one for each team involved in the game). I model the observed data using a Poisson distributions, \(y_{g}\sim\mbox{Poisson}(\theta_{g})\) with a structure on the distribution of the “scoring rates” \(\theta_{g}\): \[\log(\theta_{g})=\beta_0+\beta_1\mbox{Home}_{g}+\beta_2\mbox{Form}_{g}+\beta_3\mbox{Diff\_point}_{g}+\beta_4\mbox{Diff\_rank}_{g}+\beta_5\mbox{Days\_since\_last}_{g}+\beta_6\mbox{Tournament}_{g}+\text{att}_{g\text{Team}[g]}+\text{def}_{g\text{Opponent}[g]}.\]
There’s a bunch of “fixed effects” (in fact, I am slightly abusing the notation here: Tournament is a categorical variable and so there are in fact a set of indicators to describe the incremental effect with respect to the baseline type of tournament) and two “random effects” (\(\text{att}_{g\text{Team}[g]}\) and \(\text{def}_{g\text{Opponent}[g]}\)) that represent, respectively, the attacking strength of the first team and the defending strength of their opponent. These are modelled assuming an exchangeable structure, which implies a level of correlation across the output for the two teams involved in the same game.
The rows we want to predict are stored at the end of the dataset — in this case the number of goals scored is set to NA.
# A tibble: 72 × 17
ID date Team Opponent Goal tournament Home form diff_point diff_rank days_since_last city country rank total_points previous_points rank_date
<int> <date> <chr> <chr> <int> <chr> <dbl> <dbl> <int> <int> <dbl> <chr> <chr> <int> <int> <int> <date>
1 2657 2021-06-11 Italy Turkey NA Official 1 15.2 137 22 7 Rome Italy 7 1642 1642 2021-05-27
2 2657 2021-06-11 Turkey Italy NA Official 0 11.9 -137 -22 8 Rome Italy 29 1505 1505 2021-05-27
3 2658 2021-06-12 Switzerland Wales NA Official 0 15.5 36 4 9 Baku Azerbaijan 13 1606 1606 2021-05-27
4 2658 2021-06-12 Wales Switzerland NA Official 0 7.66 -36 -4 7 Baku Azerbaijan 17 1570 1570 2021-05-27
5 2659 2021-06-12 Denmark Finland NA Official 1 13.4 221 44 6 Copenhagen Denmark 10 1631 1631 2021-05-27
6 2659 2021-06-12 Finland Denmark NA Official 0 0 -221 -44 8 Copenhagen Denmark 54 1410 1410 2021-05-27
7 2660 2021-06-12 Belgium Russia NA Official 0 12.6 321 37 6 Saint Petersburg Russia 1 1783 1783 2021-05-27
8 2660 2021-06-12 Russia Belgium NA Official 1 7.81 -321 -37 7 Saint Petersburg Russia 38 1462 1462 2021-05-27
9 2661 2021-06-13 Croatia England NA Official 0 6.56 -81 -10 7 London England 14 1605 1605 2021-05-27
10 2661 2021-06-13 England Croatia NA Official 1 17.1 81 10 7 London England 4 1686 1686 2021-05-27
# … with 62 more rowsI used INLA to fit the model — this is very quick and I could re-use some of the code I have written for Tsakos et al. (2018), so that was handy… Leonardo has done something very similar, using rstan.
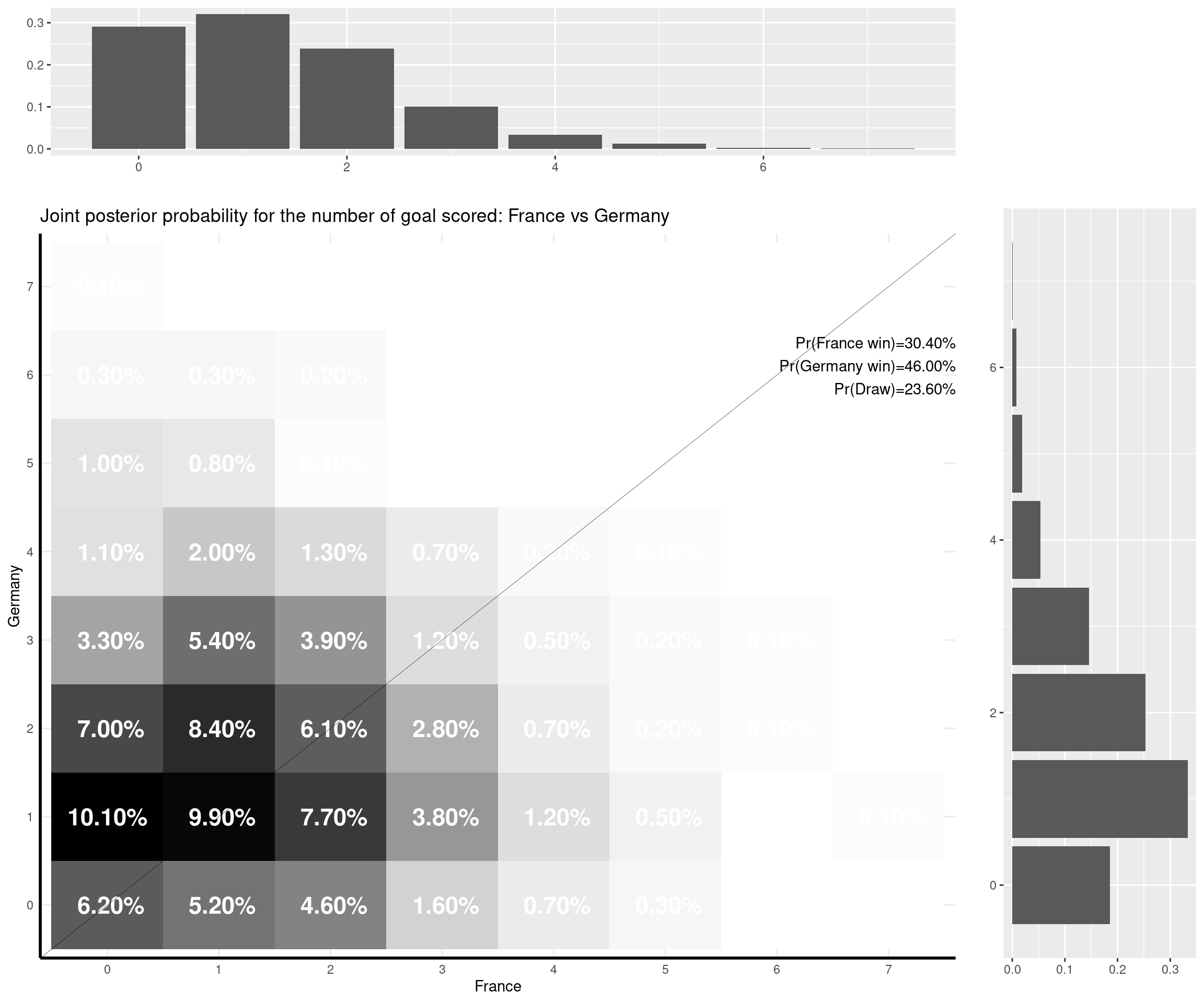
The nice thing about this model is that you can predict a weath of outputs and summarise them nicely. For instance, one important metric is of course based on the estimate of the (posterior) probability that either of the two teams would win the match, or the probability of a draw. But with the Bayesian model I set up, I can also predict the full joint posterior predictive distribution of the number of goals scored by the two teams and visualise it (together with the marginal distributions, which are depicted as the top and side histograms below).
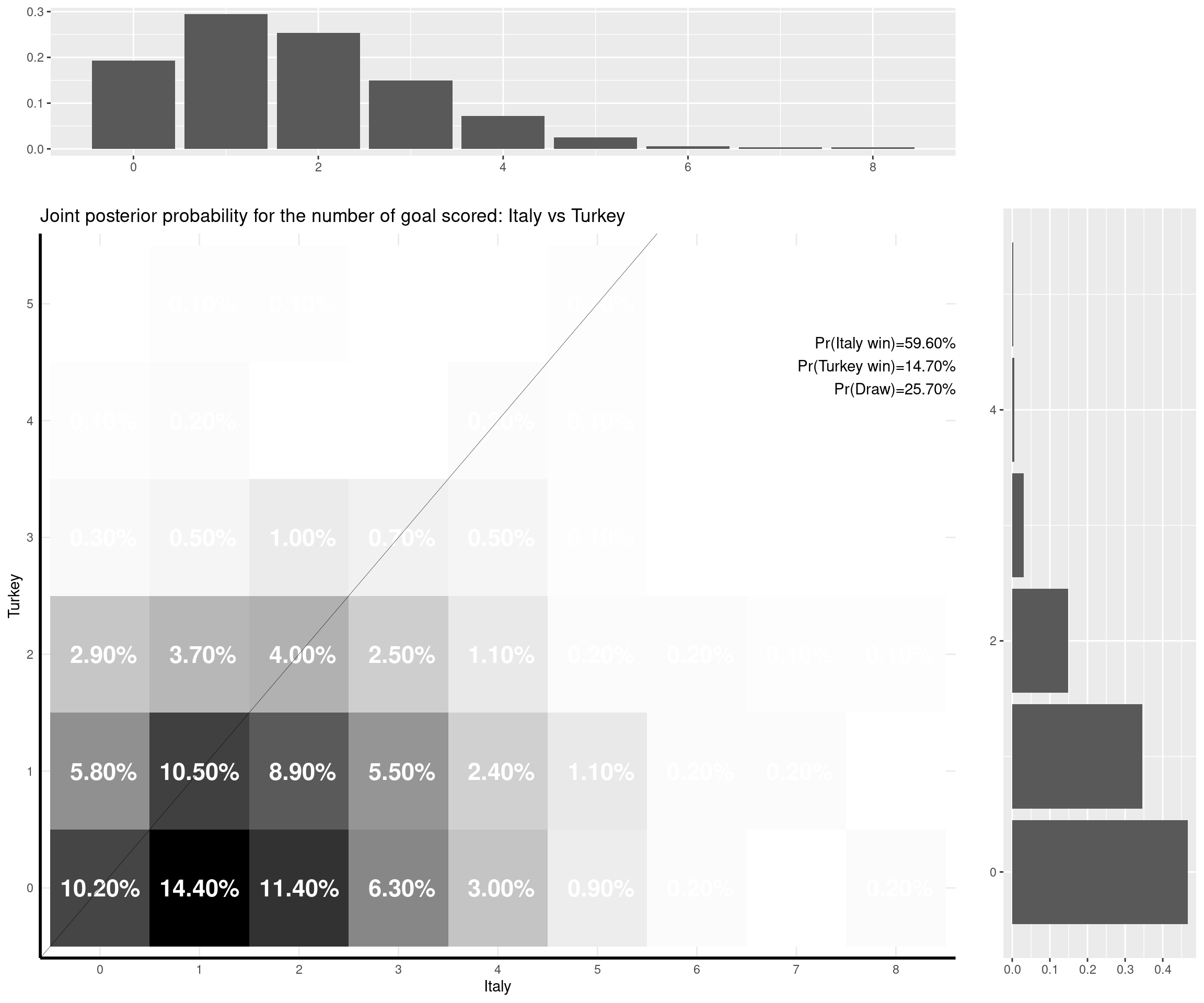
For example, the emphatic 3-0 win for Italy against Turkey was, numerically, not the most likely outcome, according to the model. The probability that Italy would win was estimated to be very high (almost 60%), but the model (and perhaps, I too) was expecting Italy to score fewer goals (the most likely outcome was a 1-0 win for Italy). The observed result was not impossible under the model (it had almost an 8% chance as opposed to a 13.5% chance for the modal result).
The prediction can be obtained for the first round of games in the Group stage (as below). As the games are played, I can update the dataset and re-run the model (which in INLA is pretty fast) to predict the next round of games (according to the historic data as well as the last performances).
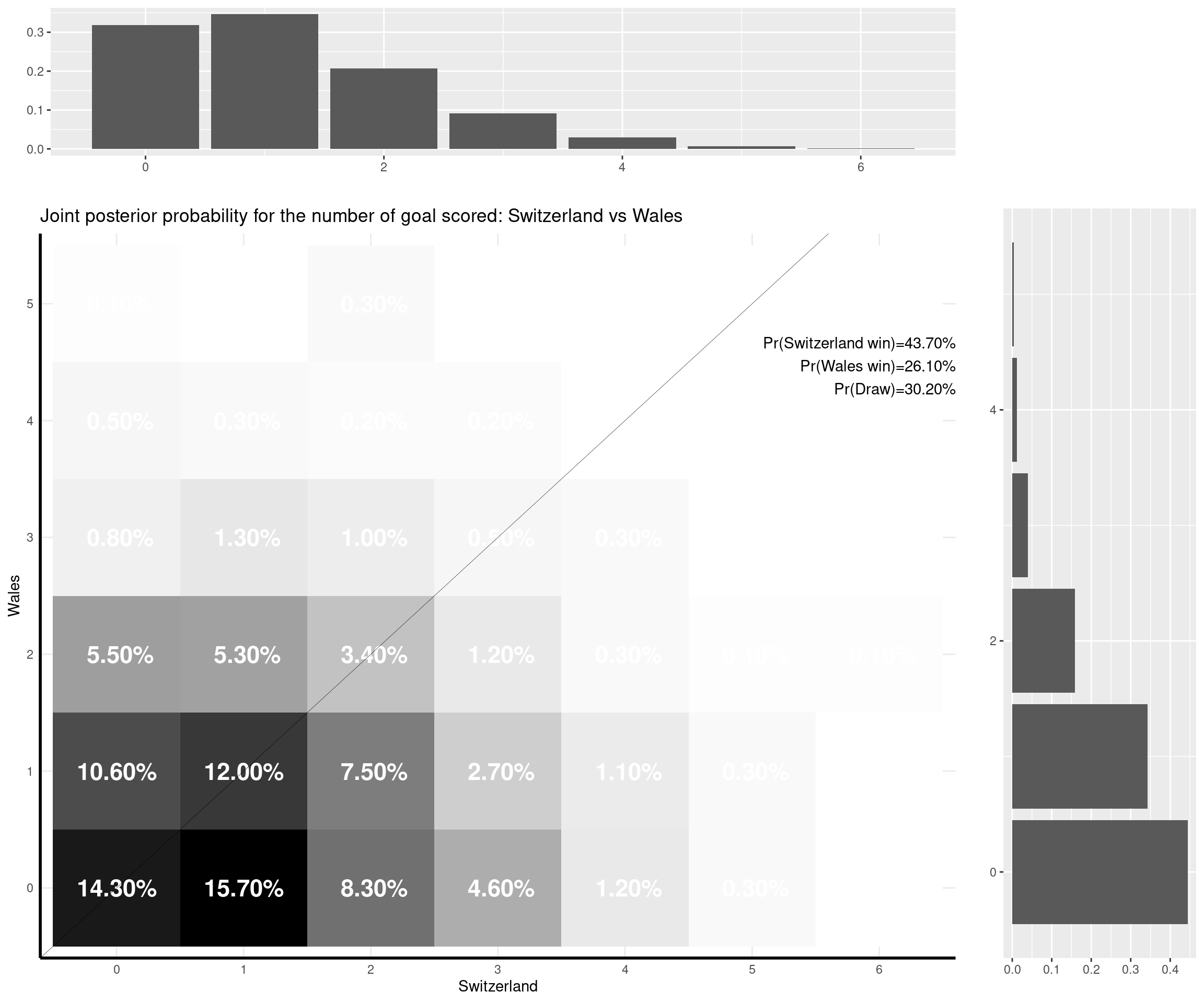
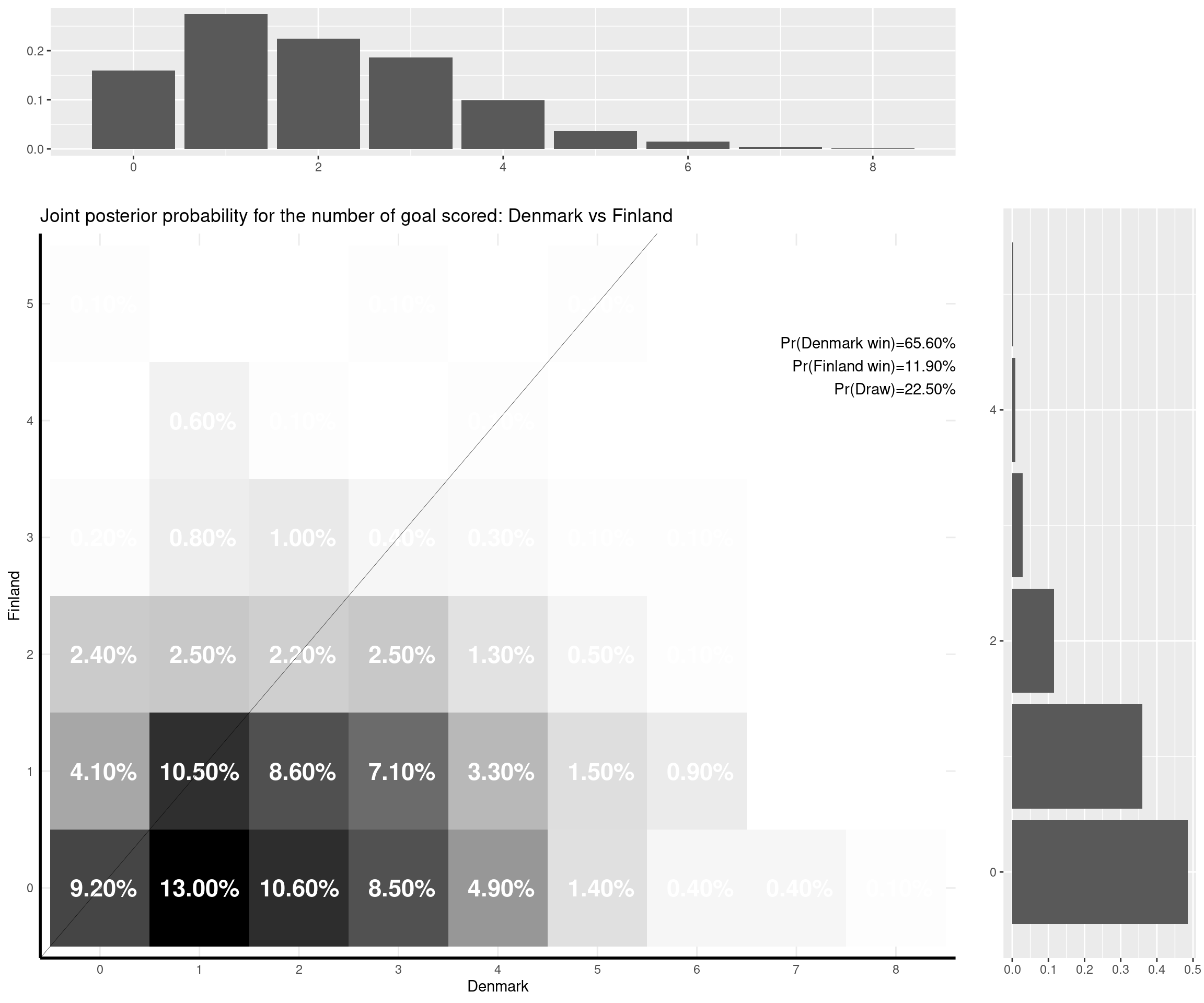
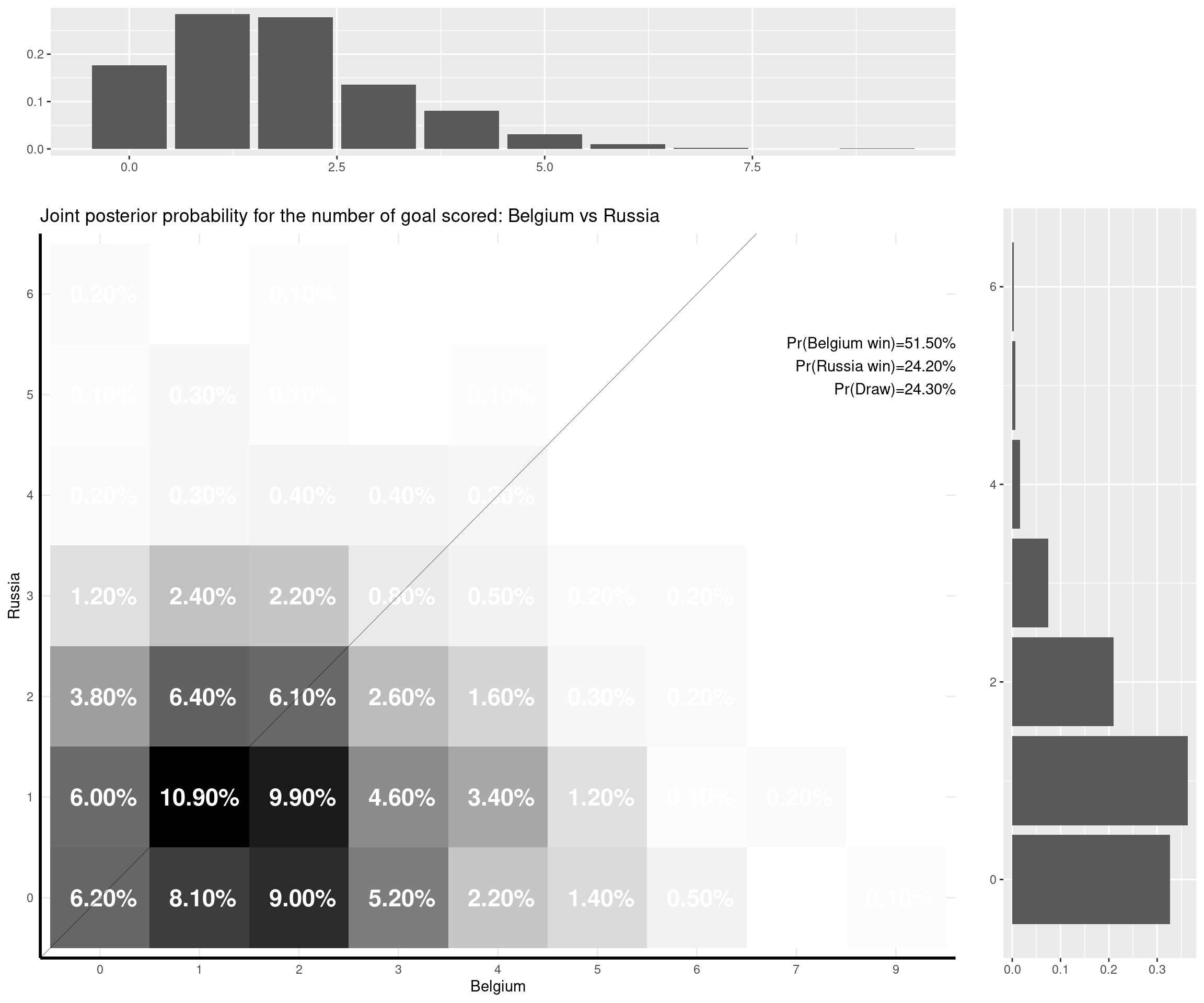
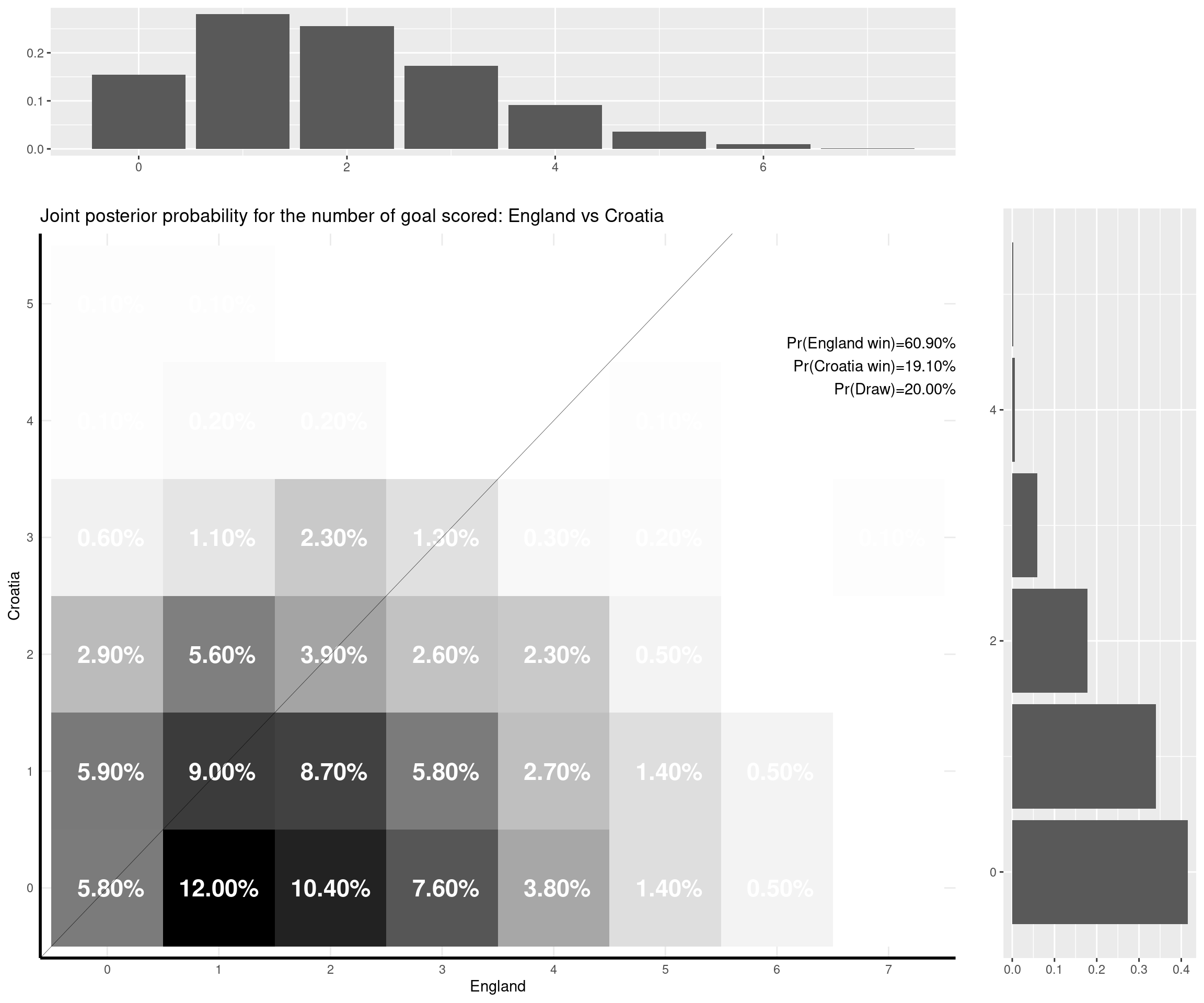
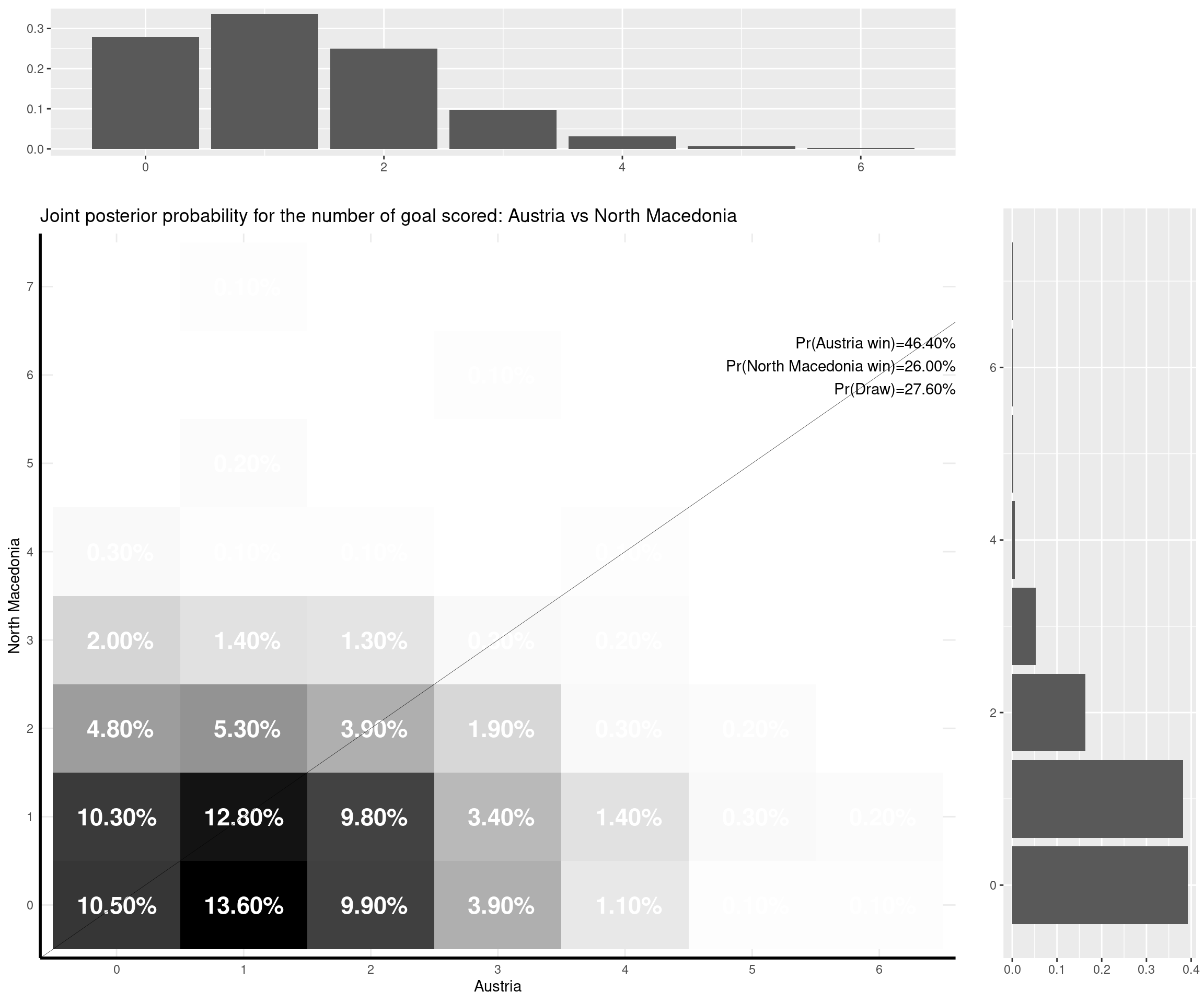
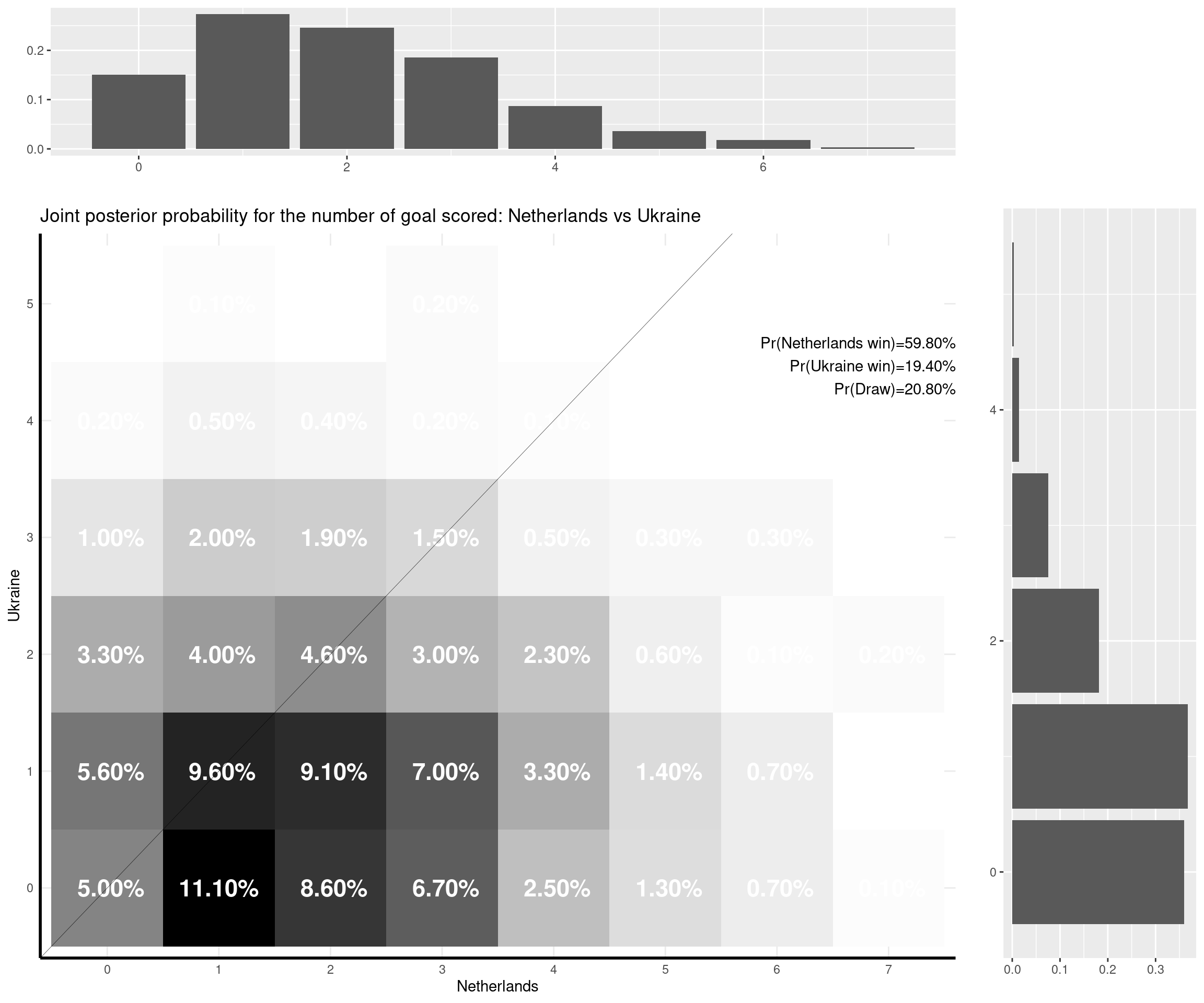
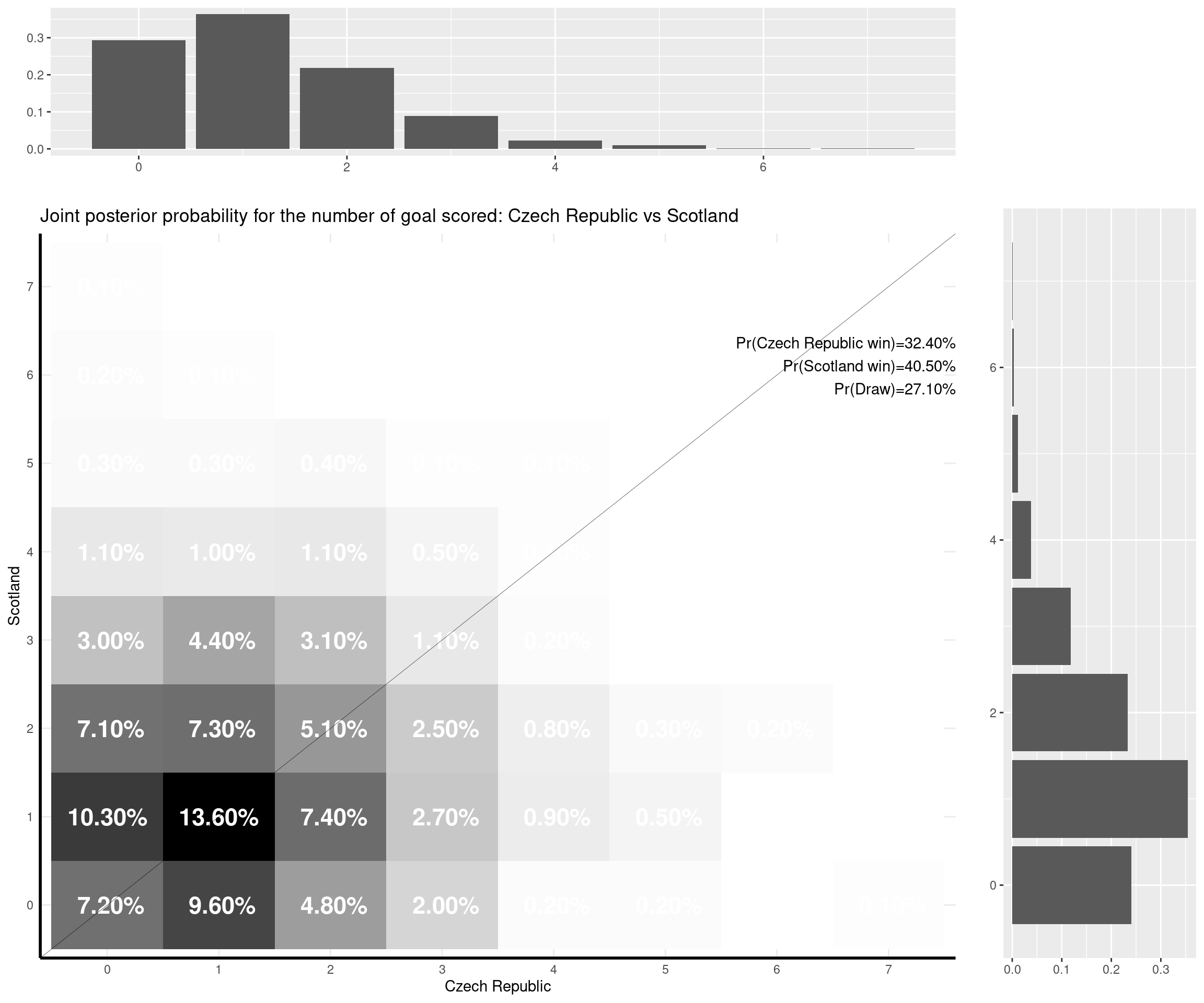
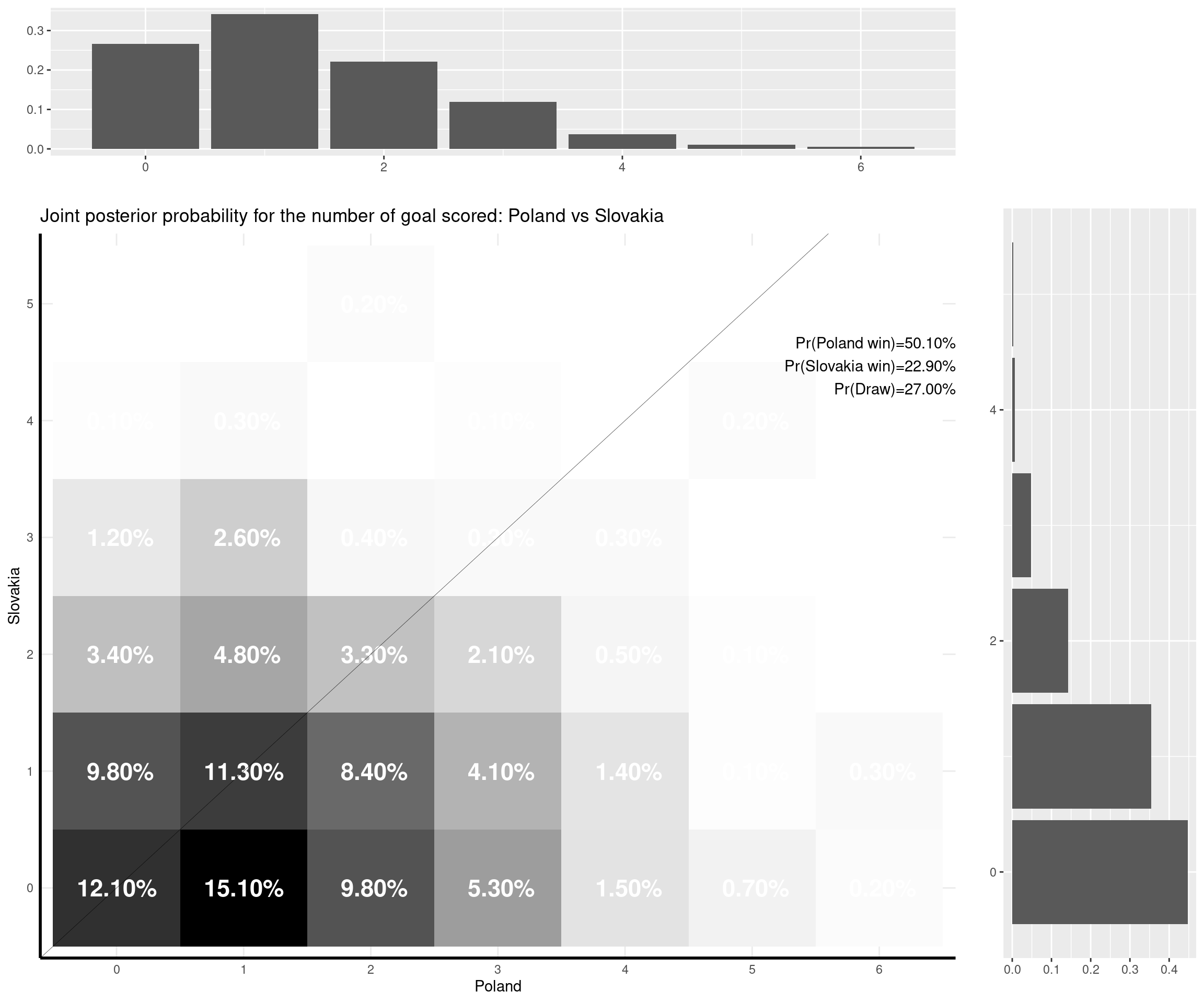
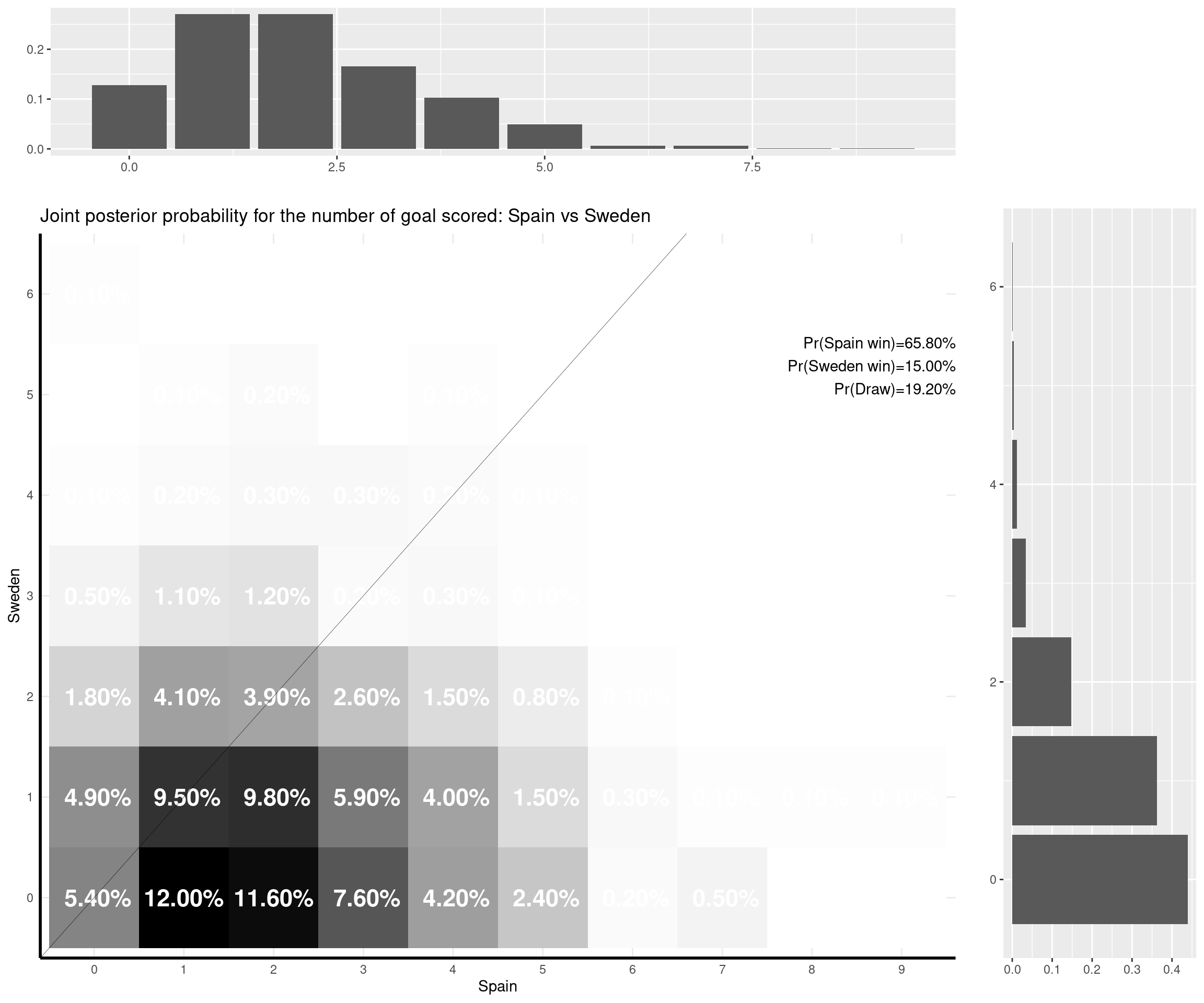
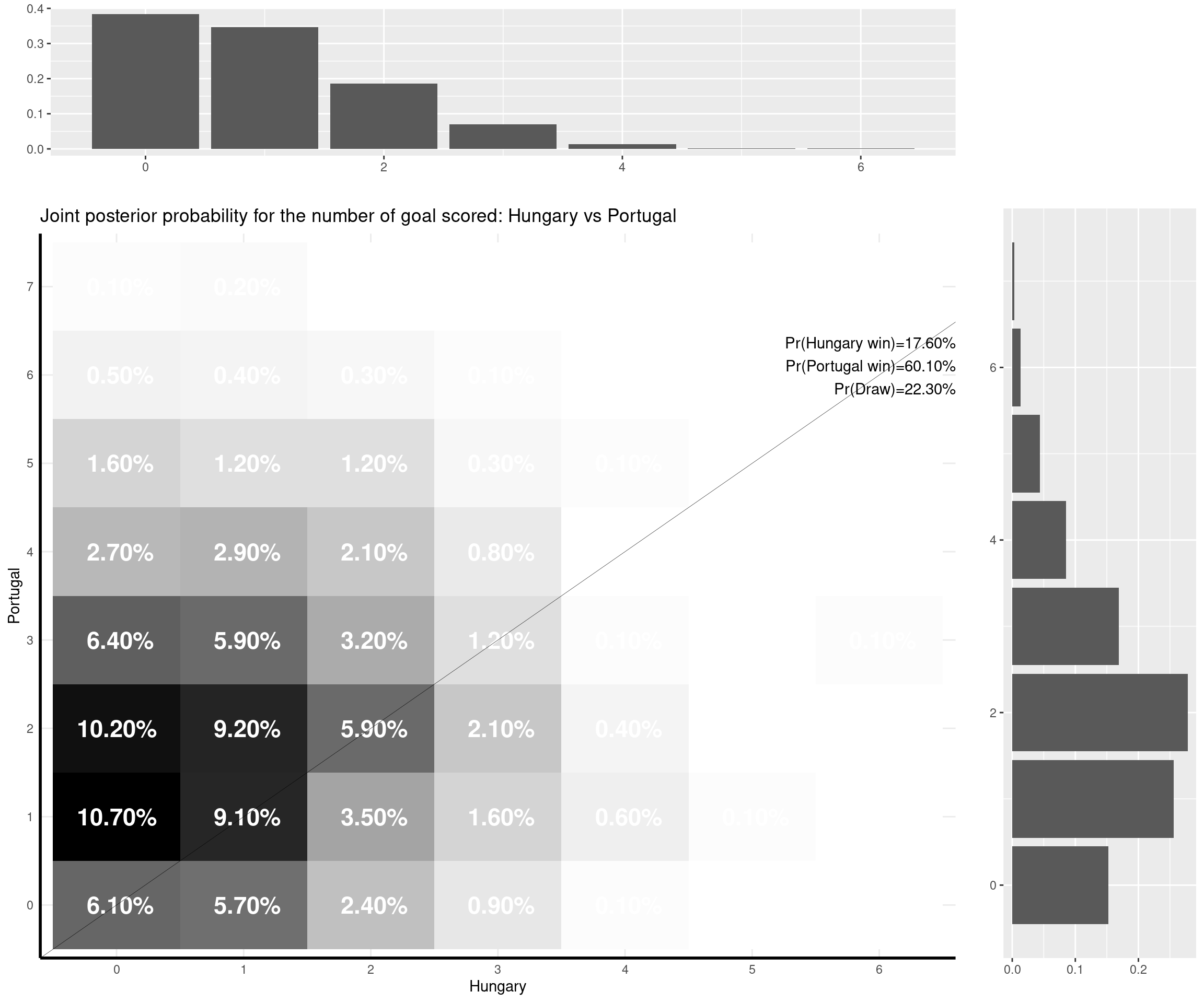
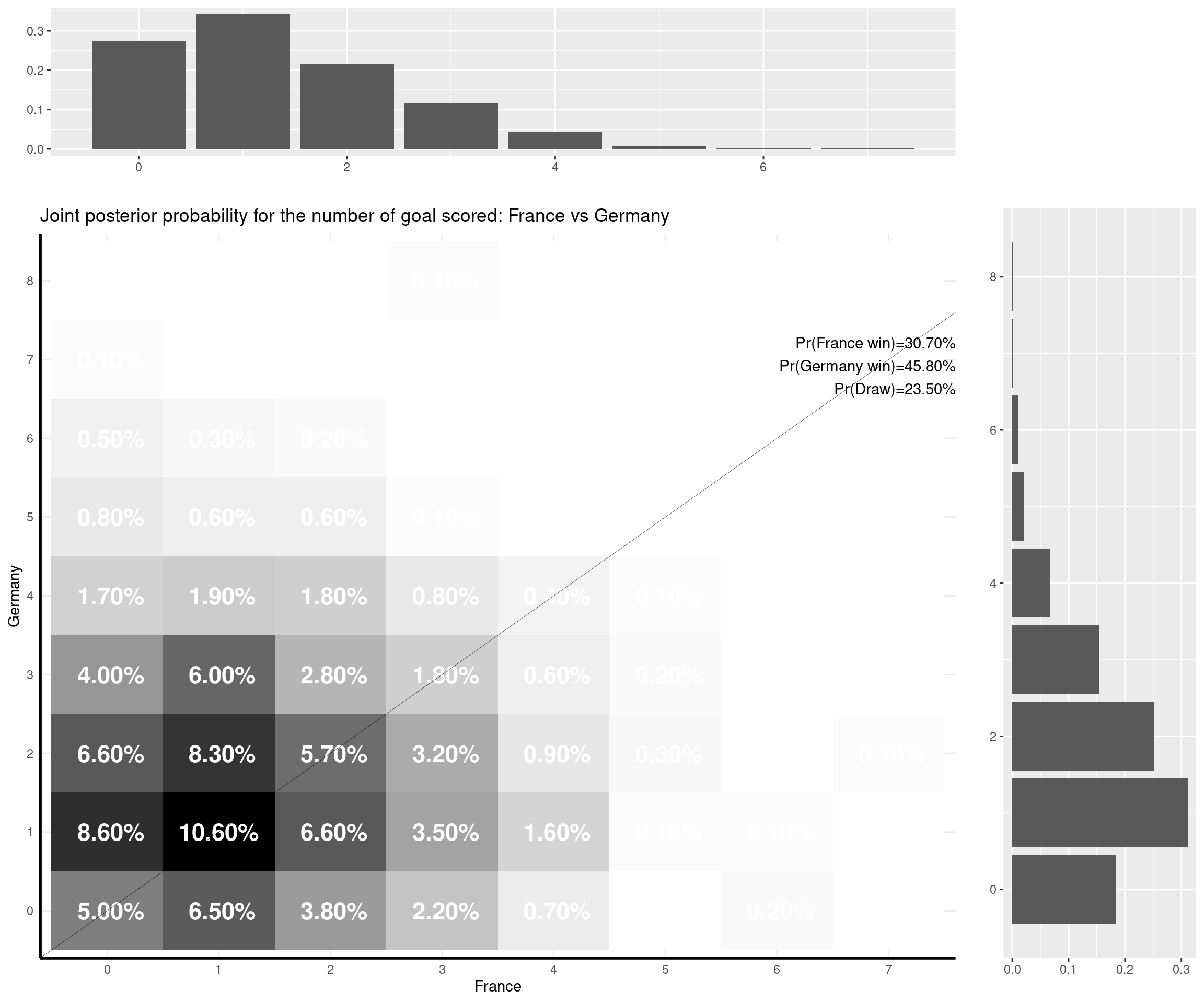
I can make some comments on the (other) games that have already been played:
- Switzerland-Wales (1-1). The model was predicting a slight higher chance of winning for Switzerland (that’s kind of contrary to Leonardo’s prediction) and was favouring a 1-0 win for them. However, both a 0-0 draw and the actual 1-1 result were relatively highly likely (with probabilities of 13.5% and 13%, respectively).
- Denmark-Finland (0-1). The model doesn’t get that right — but this was a very special game for what has happened to Christian Eriksen. The model gives the Danes the home advantage and uses the fact that they are ranked much higher than the Finn’s team and so predicts a 2-0 as the most likely outcome. The observed 0-1 was rather unlikely given the model, but again, I don’t think this game was in any way generated by the “normal” process that the model assumes…
- Belgium-Russia (3-0). That’s an interesting one — I think mostly because of the slightly over-estimation of Russian’s chances. Belgium were still favourite (with a probability of winning of over 50%), but I think in terms of prediction of the goal scored, the modal value for Russia was kind of overestimated due to the home effect (the game was played in St Petersburg), which in fact never materialised.
- England-Croatia (1-0). Here the model was bang-on. The most likely outcome was the one that was, in fact, observed. England were favourite to win by a large margin and even a bigger win (2-0) would have been supported by the model.
- Austria-North Macedonia (3-1). The actual outcome wasn’t very likely according to the model, which supported mostly a 1-0 win for the Austrian. Other outputs would have been aligned to the model’s prediction, including a 0-0 or a 1-1 draw, which probably wouldn’t have been out of North Macedonia’s grasp (they conceded two relatively late goals).
- Netherlands-Ukraine (3-2). The Dutch were highly tipped to win by the model (giving them almost a 60% chance). But the numerical outcome of the game was a lot more uncertain. A 2-0 win for Netherlands was given almost a 10% chance by the model (the Dutch were 2-0 up before the Ukraininans came back to 2-2, which was given a 4.5% chance by the model).
Of the games that are yet to be played, France-Germany is an interesting one: the model seems to suggest a very tight outcome (given they are both very strong teams) and the modal outcome is a 1-1 draw. However, it gives Germany a slightly higher chance overall — I think this is due to the fact that the game is played in Munich (so Germany take advantage of the “home effect” — though the number of fans allowed in the stadium is of course reduced…) and that Germany are historically very good in “official” competitions (e.g. the Euros or the World Cup).