
INXS
This is now borderline very old, although sadly not out of trend… In May/early June, Marta, Michela, Monica and I, together with colleagues at the Italian Statistical Institute, have worked on a paper to model the excess mortality due to COVID-19, in Italy.
I think this is something that lots of people have done/tried to do — not that we’ve done it better necessarily; but I think it’s important and interesting to realise that there is no such as thing as the “true” excess mortality (due to anything, for that matter). Because the excess is a relative measure and can be only determined in comparison to an established time trend, which is subject to uncertainty and, seems to me, by necessity needs to be modelled.
This means that it is important to try and get a reasonable model for the underlying time trend, before one can attempt at seeing the deviations from that trend — which in this case are due to the pandemic.
So: our model used the official data on the number of registered deaths at the municipality level across the years 2016–2019. In fact, for comparability with the current data (for 2020), we’ve only taken the first few months of each year. The data have been aggregated by weeks. We model \(y_{ijtk}\), the number of deaths in the \(i\)-th municipality (\(i=1,\ldots,7\,904\)), nested within the \(j\)-th province (\(j=1,\ldots, 107\)), for the \(t\)-th week (\(t=1,\ldots,17\)) and \(k\)-th year (\(k=1,\ldots,4\), with year 1 corresponding to 2016) using a Poisson distribution: \[\begin{equation} y_{ijtk} \sim \text{Poisson}\left(\mbox{E}_{ijtk}\rho_{ijtk}\right), \label{Eq:Pois} \end{equation}\] where \(\mbox{E}_{ijtk}\) represents the expected number of deaths, while \(\rho_{ijtk}\) is the mortality relative risk.
The expected number of deaths is computed by adjusting for the age structure of the population at municipality level and across the study period (internal standardisation). In particular, we calculate the national mortality rates by age group (0-14, 15-24, 25-34, 35-44, 45-54, 55-64, 65-74, 75+) over the training period (2016 – 2019); we then apply the rates to the corresponding age specific population in each municipality for the year 2016 – 2020. To obtain the weekly \(E_{ijtk}\), we sum across the age groups for each municipality and year and then divide by the number of weeks in each year, as it is commonly done in time series analyses.
As for the relative risk \(\rho_{ijtk}\), which is the main model parameter, we specify the following log-linear model: \[\begin{equation} \log(\rho_{ijtk}) = \beta_{0k} + u_i + v_i + \omega_{jt} + f(x_{it})\;. \label{Eq:linearpred} \end{equation}\] The year specific intercept \(\beta_{0k}\) is defined as \(\beta_{0k}=\beta_0 + \epsilon_k\), where \(\beta_0\) is the global intercept, representing the average mortality rate across all municipalities and years, while \(\epsilon_k\) is an unstructured random effect, i.e. \(\epsilon_k\sim \text{Normal}\left(0, \tau_\epsilon^{-1}\right)\), representing the deviation of each each from the global interecept. To take into account the spatial correlation between municipalities, we include a Besag-York-Mollie (BYM) specification. This is given by the sum of an unstructured random effect, \(v_i\sim \text{Normal}\left(0, \tau_v^{-1}\right)\) and an intrinsic conditionally autoregressive structure for \(u_i\): [ u_{i} {-i} (,n{D_i} _u);, ] where \(D_i\) is the set of neighbouring areas for the \(i\)-th municipality and \(n_{D_i}\) is its total number of neighbours.
To model the temporal trend, we specify, separately for each province, a weekly random effect \(\omega_{jt}\) through a first order random walk (RW1) with precision \(\tau_\omega\) common to all the provinces: [ {jt}{j,t-1} ({j,t-1},^{-1}) ;. ] Finally, we include in the linear predictor of Eq.\(\eqref{Eq:linearpred}\) a non-linear effect \(f(\cdot)\) of the average weekly temperature \(x_{it}\) of each municipality. In particular, we assume for \(x_{it}\) the following second order random walk (RW2) model: [ x_{it}x_{i,t-1},x_{i,t-2} (2x_{i,t-1}+x_{i,t-2},_x^{-1}) ;. ]
The following minimally informative priors are used on the hyperparameters: logGamma\((1,0.1)\) for \(\tau_u\), \(\tau_v\), \(\tau_x\) and \(\tau_\omega\); on the fixed effect \(\beta_0\) we assumed a Normal\((0,10^6)\). All the prior distributions specified in our model are relatively vague, meaning that while including some information, the overall effect is essentially to stabilise the inference, which is still mainly driven by the observed data (given the large sample size).
For the weeks in 2020, we sample from the posterior predictive distribution: [ p(y_{ijt5} ) = p(y_{ijt5} ) p()
All the inferential procedures are carried by using the Integrated Nested Laplace Approximation (INLA) approach by means of the R-INLA package (http://www.r-inla.org/). Two separate models are estimated for males and females. Once the models have been fitted to the observed data, we then use Monte Carlo (MC) simulation to obtain samples from the (approximate) joint posterior distribution of all the model parameters, including the predictions for 2020 \(p(y_{ijt5} \mid \mathcal{D})\). We use the MC samples to fully characterise the uncertainty in the estimates and predictions from our model.
Here are some of the results.
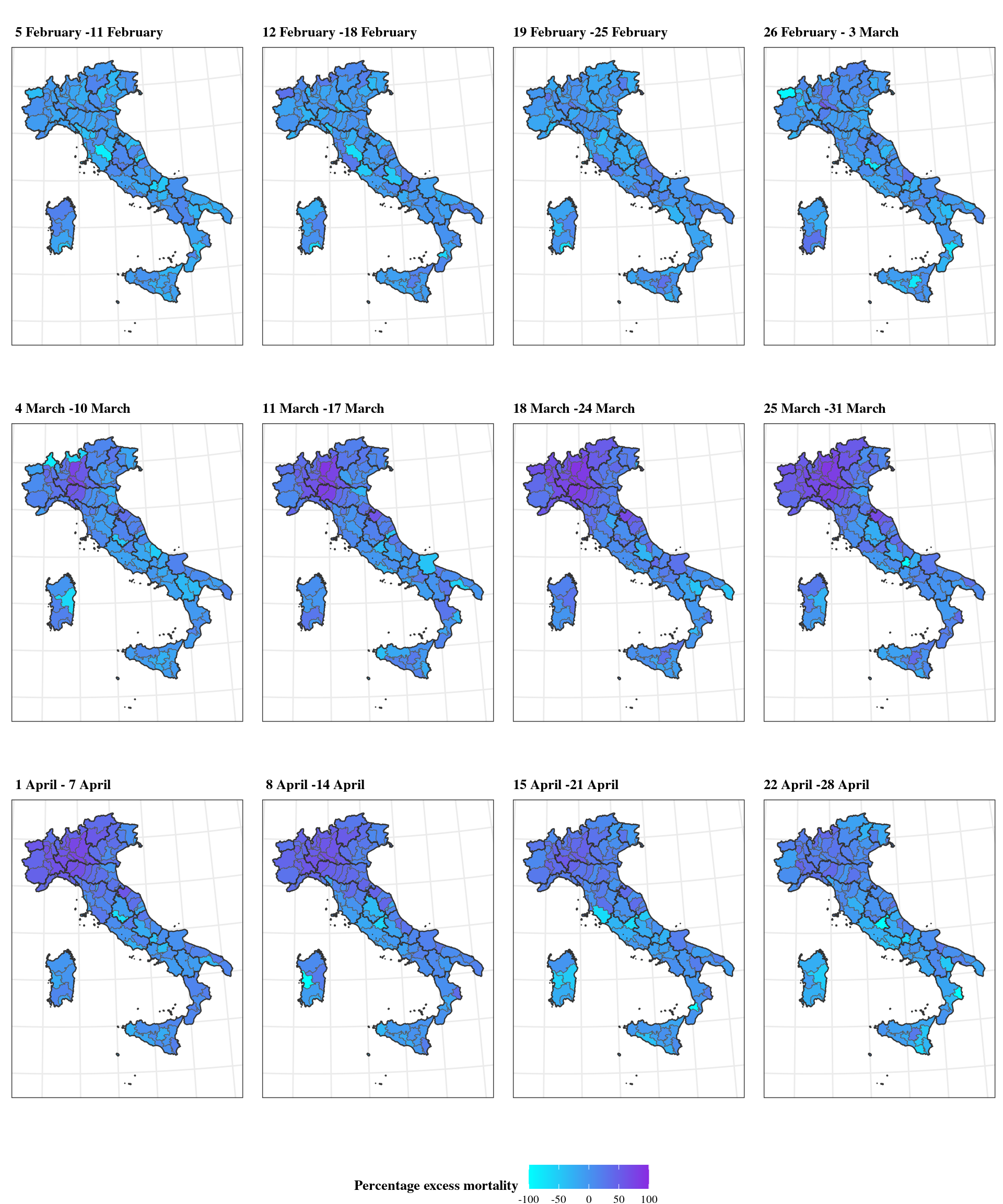
This is a map of the percent excess mortality, defined as the number of deaths from all causes relative to what it would have been expected in the absence of the COVID-19 outbreak, based on the model. The values are plotted across the provinces (using the clustering embedded in the model), over the weeks from 5 February to 28 April of 2020 (the figure shows the data for males, but females show similar, albeit slightly lower, rates). The hotspots in the regions of Lombardia and, to a lower extent, Emilia Romagna and Lombardia are visible (the darker colours, close to purple), from which the excess mortality tends to spread, mostly over Northern Italy, over time.
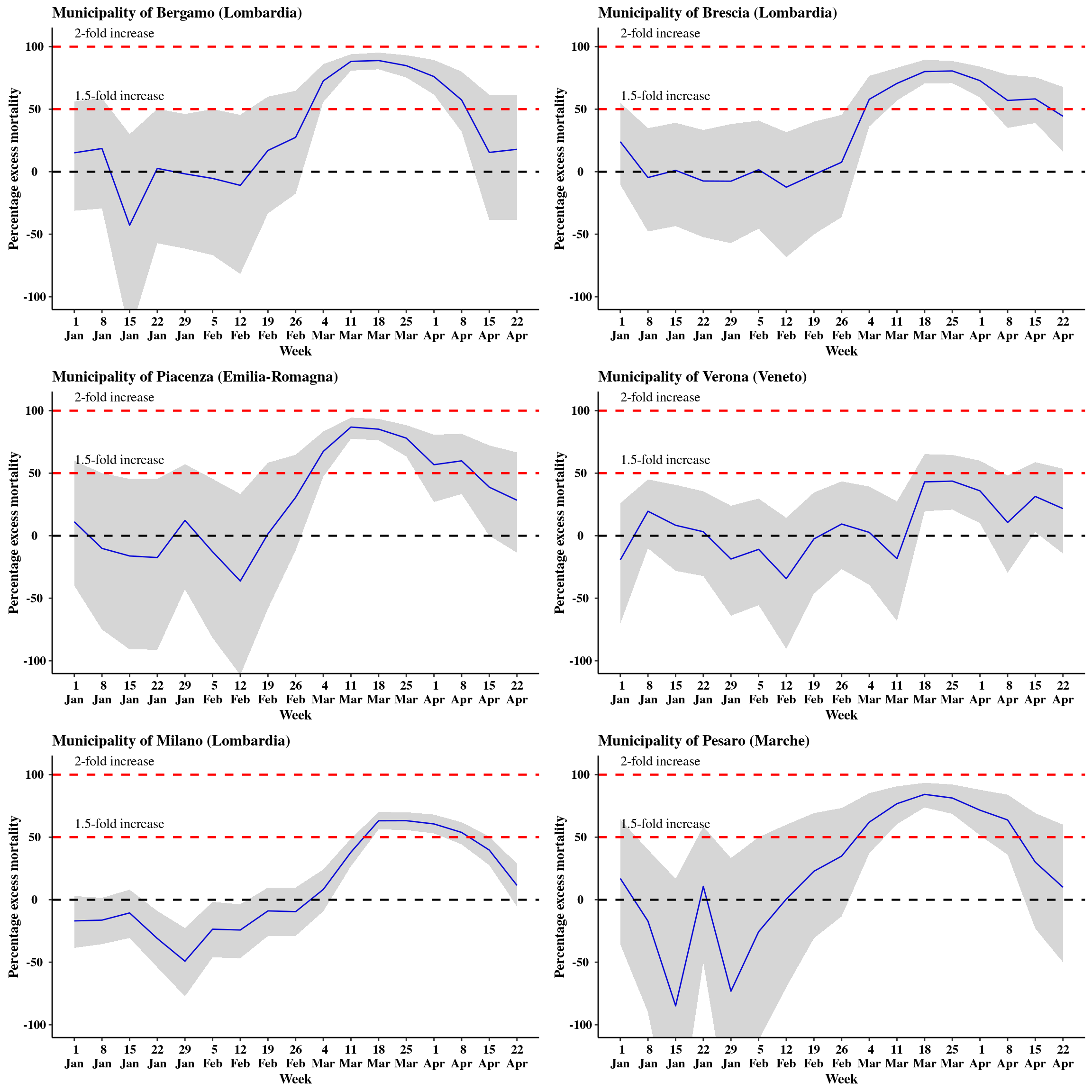
The second set of graphs shows the percentage excess mortality (in comparison to the underlying estimated trend for 2016–2019), for some selected municipalities. Some of them, particularly in the center of Lombardia (Bergamo and Brescia) show values that approaching a 2-fold increase in mortality — this is not surprising or unexpected, as these were the areas known to be more severely hit by the pandemic. The extent of the mortality that was not expected under the modelling assumptions is really scary though. Incidentally, in the first few weeks of the year, almost everywhere the trends seem to conform with the model estimates from the previous years — confirming that the model seems to get the pre-COVID trends.
We have a pre-print out and the full paper is under review now. I think the nice thing about this model is that it can be updated continuously to estimate the full extent of the excess mortality (i.e. a full posterior predictive distribution), with relatively little computational effort, once the underlying trend (which is based on a very large dataset and a relatively complex structure) has been estimated. We should be able to update our estimates using the whole year for the training set and more updated data (I think the new release with data up to June will be available shortly) soon.