Prosecutor’s fallacy — Brexit style
When it comes to Brexit, I’m finding harder and harder to concentrate and either pretend that nothing bad is happening or actually acknowledging all the madness going around (which, when I do, almost invariably makes me rather angry)…
Anyway: the other day, this exchange caught my eye. Now, I am fully aware I am biased towards the people who think Brexit is possibly the most stupid idea ever. But, I don’t really know much about Will Self (other than in this story he represents the “Remainers”); and I don’t know much (although, arguably, a lot more than I wish I had to) about Mark Francois (the “Brexiteer”). Basically, their sort of scary encounter was based on the following exchange:
Will Self (WS): Every racist and anti-Semite in the country pretty much probably voted for Brexit.
Mark Francois (MF): You’ve basically tried to slur anybody who voted Leave as a bigot.
Now, this is a classical case of “prosecutor’s fallacy” — what WS is making is an assessment of \(\Pr(L\mid R)\) (where \(L=\) “Voted Leave” and \(R=\) “Racist or anti-Semite”) and what MF hears (either because he genuinely doesn’t understand the difference or because he chooses not to for political reasons — I don’t know. I really don’t like the guy, so am happy to even go with the former. But I digress and either way he gets it wrong, so it doesn’t matter…) is \(\Pr(R\mid L)\).
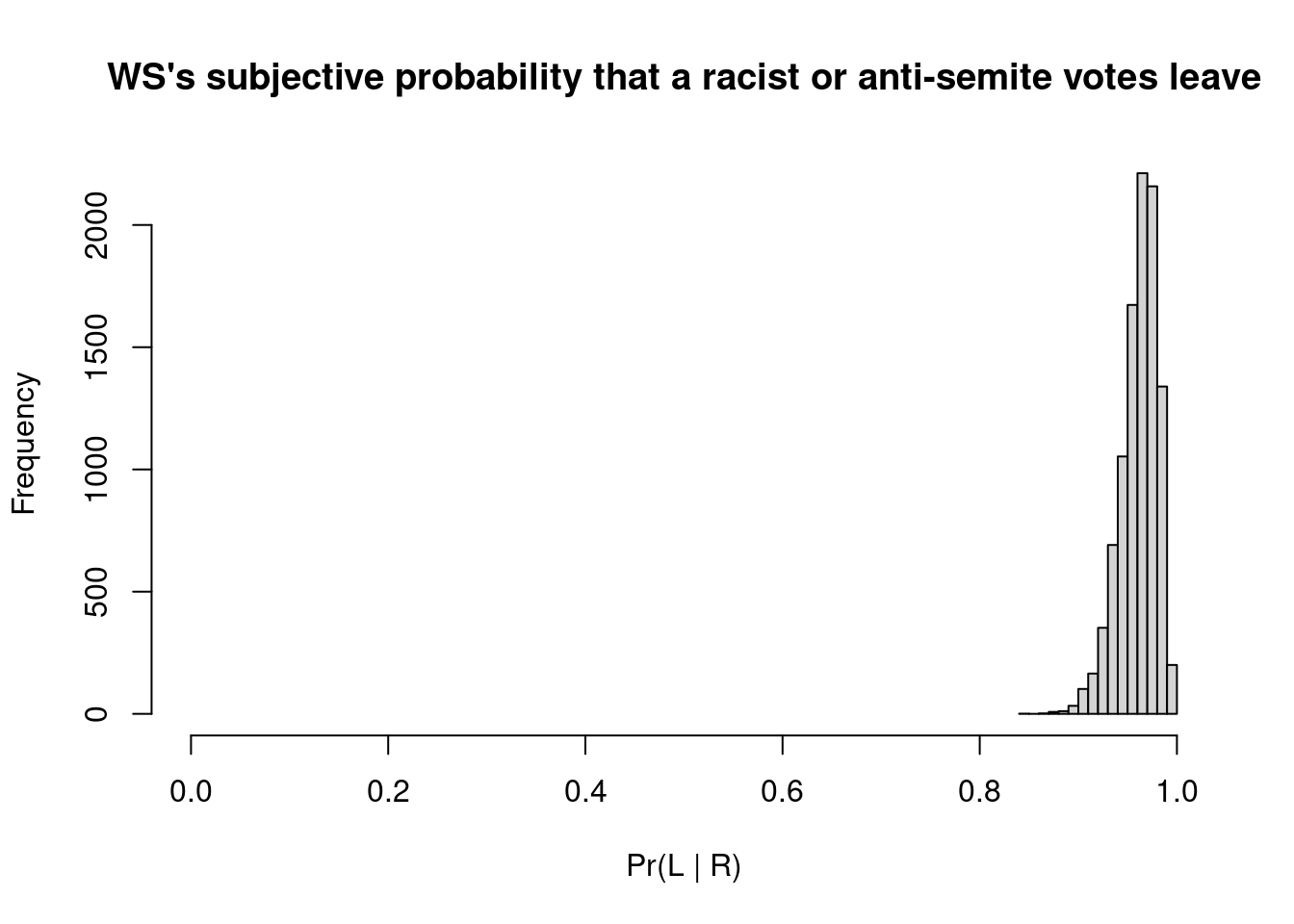
But these two are quite different! So: first things first. The point here is a classic application of Bayes’ theorem \[\Pr(R\mid L) = \frac{\Pr(L \mid R)\Pr( R )}{\Pr(L)}.\] The easy bit is the marginal probability of Leave vote, which is a known quantity — that’s simply the proportion of voters at the referendum who went the wrong way (oops… Sorry. I mean who voted Leave! [NB: for the avoidance of doubt, this is genuinely meant to be a joke]): \[\Pr(L) = \frac{17410742}{17410742+16141241}=0.5189.\] In the exchange, MF (this time, rightly so) asks WS “How do you know that in a secret ballot?”. Like I said, that’s a fair point, to which WS replies “I suspect it”. You may agree or not with the general statement, but for instance, we can try and elicit WS’s assessment using some kind of probability distribution centered somewhere very close to 1, to allow for some uncertainty. For example, we may model \(\Pr(L\mid R) \sim \mbox{Beta}(99,4)\). This implies a picture like the following.
(I suppose, to be precise, I should clarify that this isn’t necessarily WS’s subjective probability — rather is my own subjective interpretation of WS’s subjective probability…).
So in order to conclude what MF has we really need another bit of information — that’s an estimate of the proportion of racists and anti-Semites in the general population, \(\Pr( R )\). Now there may be actual data and estimates (which I am not even beginning to search for). Instead, I think what can be easily done is to do some kind of “sensitivity analysis” by varying the value of \(\Pr( R )\) in a suitable range and then checking what happens to the probability of interest \(\Pr(R \mid L)\).
That’s easily done in a sort of Monte Carlo simulation framework.
# Simulates from the subjective distribution of leavers among racists/anti-Semites
lmidr = rbeta(10000,99,4)
# Defines the marginal probability of voting leave
l = 17410742/(17410742+16141241)
# Defines a range of potential values for the probability of somebody being racist/anti-Semite
r = seq(0,.5,.001)
# Computes the posterior probability (what MF wants)
rmidl=matrix(NA,length(lmidr),length(r))
for(i in 1:length(r)) {
rmidl[,i]=(lmidr*r[i])/l
}Interestingly, because of how the problem is set up and the assumed relationships among the variables of interest, basically we have a natural upper limit for the probability that a random individual is racist or anti-Semite. This is of course because by necessity the ratio on the right-hand side of Bayes’ theorem has to be bounded by 1 (as it represents a probability). And so I don’t need to consider all possible scenarios for \(\Pr( R )\) between 0 and 1 — I can stop at 0.5 (and that’s of course 0.5 larger than it should ever be!).
The code above computes, for each assumed value of \(\Pr( R )\) in [0; 0.5] the resulting distribution \(\Pr(R\mid L)\) obtained by combining the uncertainty in \(\Pr(L\mid R)\) to that of \(\Pr( R )\) and \(\Pr(L)\).
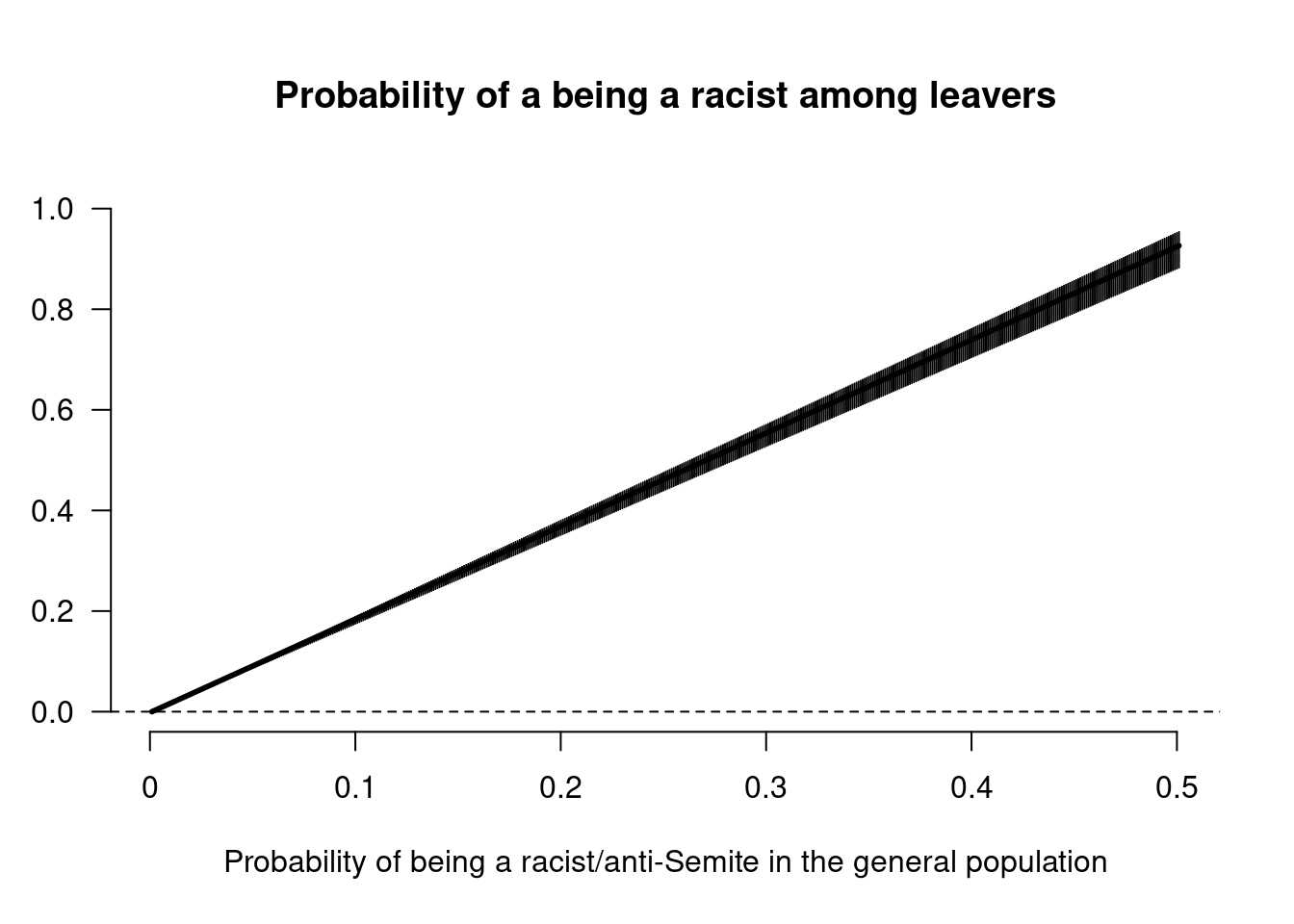
The graph above shows a summary of the underlying probability distribution for \(\Pr(R\mid L)\) in correspondence of each assumed value for \(\Pr( R )\) — reading across the \(x-\)axis you can see a measure of the spread of the distribution in terms of the 95% interval estimate. So, even by assuming that virtually every racist had voted Leave, what WS was implying is that a proportion of Leave voters (that can be as little as 0, in the ideal case where nobody is racist in the general population), to about 20% if 10% of the general population is, to virtually all if the proportion of racists/anti-Semites in the population were as high as 50%.
There’s of course a lot more to the story than the simple prosecutor’s fallacy — I honestly have no idea whether all racists/anti-Semites would in fact be Leavers. I too suspect the proportion might be very high, but that’s besides the point. I think what really matters is that politicians have no excuse for ignorance of these things, particularly when they try and score political points off them…