Face value

I found a little more time to think about the election model and fiddle with the set up, as well as use some more recent polls \(-\) I have now managed to get 9 polls detailing voting intention for the 7 main parties competing in England, Scotland and Wales.
I think one thing I was not really happy with the basic set up I’ve used so far is that it kind of takes the polls at “face value”, because the information included in the priors is fairly weak. And we’ve seen in recent times on several occasions that polls are often not what they seem…
So, I’ve done some more analysis to: 1) test the actual impact of the prior on the basic setting I was using; and 2) think of something that could be more appropriate, by including more substantive knowledge/data in my model.
First off, I was indeed using some information to define the prior distribution for the log “relative risk” of voting for party \(p\) in comparison to the Conservatives, among Leavers (\(\alpha_p\)) and Remainers (\(\alpha_p + \beta_p\)), but I think that kind of information was really weak. It is helpful to run the model by simply “forward sampling” (i.e. pretending that I had no data) to check what the priors actually imply. As expected, in this case, the prior vote share for each party was close to basically \((1/P)\approx 0.12\). This is consistent with a “vague” structure, but arguably not very realistic \(-\) I think nobody is expecting all the main parties to get the same share of the vote before observing any of the polls…
So, I went back to the historical data on the past 3 General Elections (2005, 2010 and 2015) and used these to define some “prior” expectation for the parameters determining the log relative risks (and thus the vote shares).
There are obviously many ways in which one can do this \(-\) the way I did it is to first of all weigh the observed vote shares in England, Scotland and Wales to account for the fact that data from 2005 are likely to be less relevant than data from 2015. I have arbitrarily used a ratio of 3:2:1, so that the latest election weighs 3 times as much as the earliest. Of course, if this was “serious” work, I’d want to check sensitivity to this choice (although see below…).
This gives me the following result:
Conservative 0.366639472 Green 0.024220681 Labour 0.300419740 Liberal Democrat 0.156564215 Plaid Cymru 0.006032815 SNP 0.032555551 UKIP 0.078807863 Other 0.034759663
Looking at this, I’m still not entirely satisfied, though, because I think UKIP and possibly the Lib Dem may actually have different dynamics at the next election, than estimated by the historical data. In particular, it seems that UKIP has clear problems in re-inventing themselves, after the Conservatives have by and large so efficiently taken up the role of Brexit paladins. So, I have decided to re-distribute some of the weight for UKIP to the Conservatives and Labour, who were arguably the most affected by the surge in popularity for the Farage army.
In an extra twist, I also moved some of the UKIP historical share to the SNP, to safeguard against the fact that they have a much higher weight when it counts for them (ie Scotland) than the national average suggests. (I could have done this more correctly by modelling the vote in Scotland separately).
These historical shares can be turned into relative risks by simply re-proportioning them by the Conservative share, thus giving me some “average” relative risk for each party (against the reference \(=\) Conservatives). I called these values \(\mu_p\) and have used them to derive some rather informative priors for my \(\alpha_p\) and \(\beta_p\) parameters.
In particular, I have imposed that the mixture of relative risks among leavers and remainers would be centered around the historical (revisited) values, which means I’m implying that \[\hat{\phi}_p = 0.52 \phi^L_p + 0.48 \phi^R_p = 0.52 \exp(\alpha_p) + 0.48\exp(\alpha_p)\exp(\beta_p) \sim \mbox{Normal}(\mu_p,\sigma).\] If I fix the variance around the overall mean \((\sigma^2)\) to some value (I have chosen 0.05, but have done some sensitivity analysis around it), it is possible to do some trial-and-error to figure out what the configuration of \((\alpha_p,\beta_p)\) should be so that on average the prior is centered around the historical estimate.
I can then re-run my model and see what the differences are by assuming the “minimally informative” and the “informative” versions.

Here, the black dots and lines indicate the mean and 95% interval of the minimally informative prior, while the blue dots and lines are the posterior estimated vote shares (ie after including the 9 polls) for that model. The red and magenta dots/lines are the prior and posterior results for the informative model (based on the historical/subjective data).
Interestingly, the 9 polls seem to have quite substantial strength, because they are able to move most of the posteriors (eg the Conservatives, Labour, SNP, Green, Plaid Cymru and Other). The differences between the two versions of the model are not huge, necessarily, but they are important in some cases.
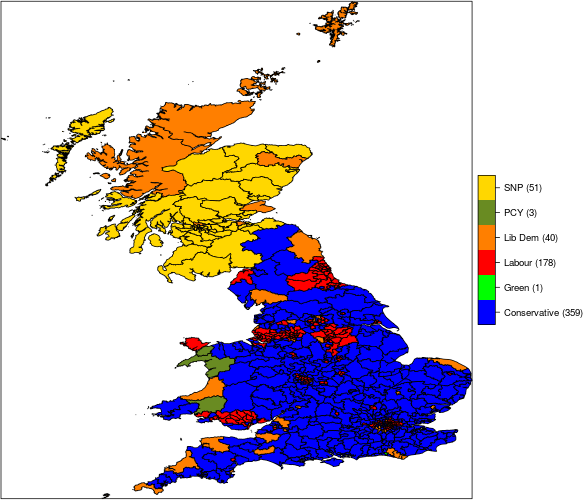
The actual results in terms of seats won are as in the following. Party Seats (MIP) Seat (IP) Conservative 371 359 Green 1 1 Labour 167 178 Lib Dem 30 40 Plaid Cymru 10 3 SNP 53 51
Substantively, the data + model assumptions seem to suggest a clear Conservative victory in both versions. But the model based on informative/substantive prior seems to me a much more reasonable prediction \(-\) strikingly, the minimally informative version predicts a ridiculously large number of seats for Plaid Cymru.
The analysis of the swing of votes is shown in the following (for the informative model). 2015/2017 Conservative Green Labour Lib Dem PCY SNP Conservative 312 0 0 17 0 1 Green 0 1 0 0 0 0 Labour 45 0 178 8 0 1 Liberal Democrat 0 0 0 9 0 0 Plaid Cymru 0 0 0 0 3 0 SNP 1 0 0 6 0 49 UKIP 1 0 0 0 0 0
Labour are predicted to now win any new seats and their losses are mostly to the Conservatives and the Lib Dems. This is how the seats are predicted across the three nations.
As soon as I have a moment, I’ll share a more intelligible version of my code and will update the results as new polls become available.