The Oracle (7)
We’re now down to 8 teams left in the World Cup. Interestingly, despite a pretty disappointing display by some of the (more or less rightly so) highly rated teams, such as Spain, Italy, Portugal or England, European sides are exactly 50% of the lot. Given the quarter final game between France and Germany, at least one European team is certain to reach the semifinals. Also, it is worth noticing that the 8 remaining teams are the group winners \(-\) which kind of confirms Michael Wallace’s point.
We’ve now re-updated the data, the “form” and the “offset” variables (as briefly explained here) using the results of the round of 16. The model had predicted (as shown in the graphs here) wide uncertainty for the potential outcomes of the games (also, we had not included the added complication of extra times & penalties \(-\) more on this later). I believe this has been confirmed by the actual games. In many cases (in fact, probably all but the Colombia-Uruguay game, which was kind-of-dominated by the former), the games have been substantially close. As a result, we’ve observed a slightly higher than usual proportion of games ending up at extra times.
So, we’ve also complicated (further!) our model to estimate the result by including extra times and penalties. In a nutshell, when the game is predicted to be a draw (ie the predicted number of goals scored by the two teams is the same), then we’ve additionally simulated the outcome of extra times.
In doing this, we’ve used the same basic structure as for the regular time, but we’ve added a decremental factor to the linear predictor (describing the “propensity” of team A to score when playing against team B). This makes sense, since the duration of extra time is 1/3 of the normal game. Also, there is added pressure and teams normally tend to be more conservative. Thus, in this prediction, we’ve increased the chance of observing 0 goals and accounted for the shorter time played. If the prediction is still for a draw, then we’ve determined the winner by assuming that penalty shoot outs essentially are a randomising device \(-\) each team have 50% chance of winning them.
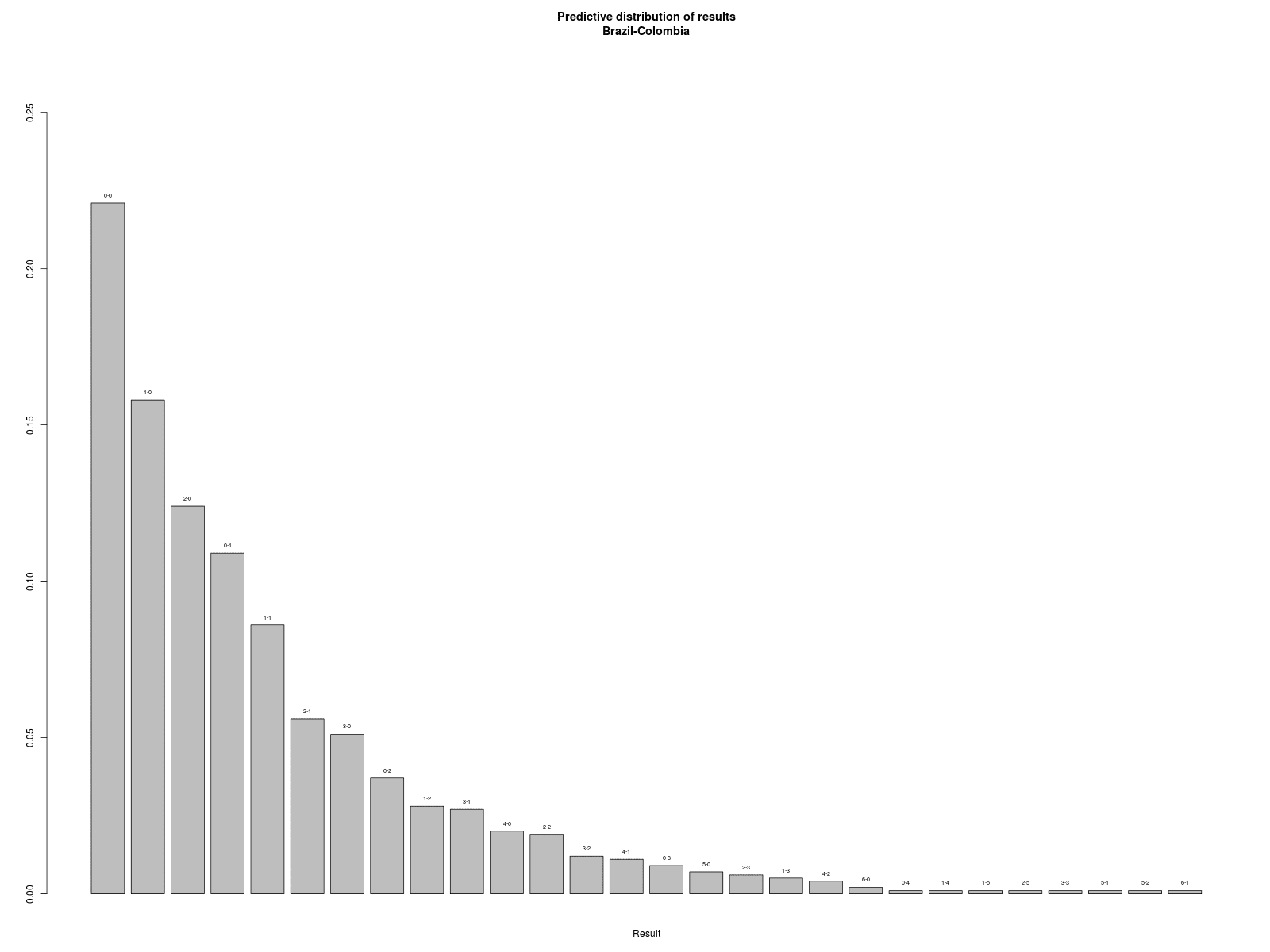
These are the contour plots for the posterior predictive distribution of the goals scored in the quarter finals, based on our revised model.
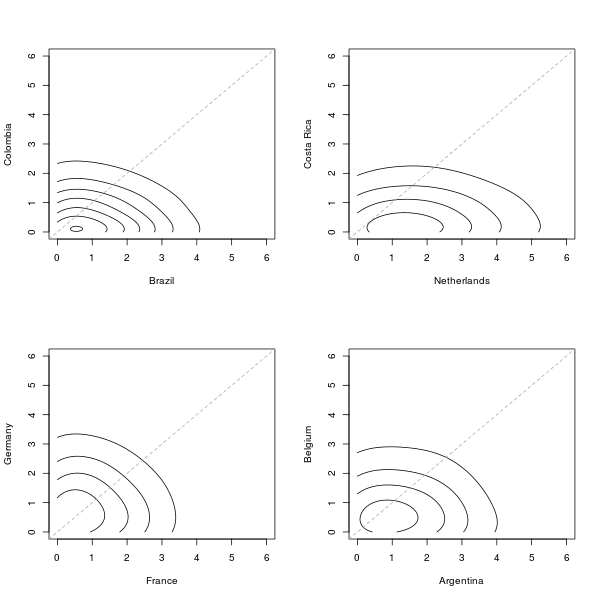
Basically all games are again quite tight \(-\) perhaps with the (reasonable?) exception of Netherlands-Costa Rica in which the Dutch are favourite and predicted to have a higher chance of scoring more goals (and therefore winning the game).

As shown in the above graph, draws are quite likely in almost all the games; the European derby is probably the closest game (and this seems to make sense given both the short- and long-term standing of the two teams). Brazil and Argentina both face tough opponents (based on the model \(-\) but again, in line with what we’ve seen so far).
Using the result of the model in terms of prediction of the results at extra time & penalties, we estimate the overall probability of winning the game (ie either within 90 minutes or beyond) as
| Brazil | Colombia | 0.657 | 0.343 |
| Netherlands | Costa Rica | 0.776 | 0.224 |
| France | Germany | 0.497 | 0.503 |
| Argentina | Belgium | 0.607 | 0.393 |
(in the above table, the third and fourth columns indicate, respectively, the predicted chance that the team in column one and two, respectively, win the game and progress to the semifinals).
One final remark, which I think it’s generally interesting, is that by the time we’ve reached the quarter finals, the value of the “current form” variable for Brazil (who started as hot favourites based on the evidence synthesis of the published odds that we’ve used to define it at the beginning of the tournament) is lower than that of their opponent. But again, Colombia have sort of breezed through all of their games so far, while Brazil have kind of stuttered and have not won games that they probably should have (taking at face value their “strength”). This doesn’t seem enough to make Colombia favourites in their game against the host \(-\) but beware of surprises! After all, the distribution of the possible results is not so clear cut…