The Oracle (1)

This is the first follow up to our previous, (slightly technical and detailed) post on the World Cup prediction. First off a quick and simplified recap on the model and then off with some prediction!

So: the idea is to use a collection of data to estimate a measure of “propensity” of a team \(t\) to score when they play an opponent \(s\). The estimation is done by considering a set of data on several types of games: in particular, we use the data on the last 6 World Cups and the last 4 years (including friendlies, qualifiers, continental finals and last year’s Confederations Cup). We can use this “propensity” to predict the number of goals scored by any two teams in the next game they play against each other.

A crucial point is that the observed number of goals scored by \(t\) and \(s\) respectively will tend to be correlated (of course, this correlation may not be extremely large, but on average we can expect better teams to score more and concede fewer goals than lesser teams). We account for this correlation in our model by using structured (“random”) team-specific effects.

Another important point is that how well a team will perform will reasonably depend (although not in a deterministic way!) by a measure of “current form” and, even more importantly, by the difference in this domain between the two teams. Because the World Cup is a relatively short and volatile event, in our prediction we start by estimating the 32 participants strength using published bookmakers’ odds data.

So, based on the long-run trend (estimated using our model and the available data, covering a relatively long time horizon) and the current level of form/strength (estimated from a combination of data from the bookies), we could predict the number of goals scored in all the games. In fact, here’re our predicted probabilities of progressing to the knockout stage (the first stage is played in 8 groups, each made by 4 teams, playing each other once; the top two teams go through).

In many of the groups, there is a relatively clear-cut situation. Brazil (Group A), Spain (Group B), Argentina (Group C) and Germany (Group G) are clear favourite to progress (and indeed to win their own groups). France seem to have the edge in Group E, where Ecuador and Switzerland should battle for the second available spot; Portugal shouldn’t have too many problems qualifying in Group G; the Netherlands should overcome Chile and grab the second available spot in Group B. Group D is the most uncertain, with Uruguay, England and Italy all being estimated to have a very similar chance of progressing through. I think these results are in line with other models (which we also have mentioned here).

But this prediction doesn’t make an awful lot of sense, I think. In fact, the main assumption underlying this model is that the strength/form of each team remains constant throughout the three games of the first stage. I don’t really believe this assumption \(-\) it seems to me that how teams approach the next game will strongly depend on how they’ve done in their previous one(s).

So what we’ll do is to make predictions a bit at a time. The first stage can be effectively divided into three rounds, each made by 16 games; at the end of the first 16 games, all 32 teams will have played once; at the end of the second 16 games, all will have played twice; and of course by game 48 all have played their three games. Our strategy is to:

1. Predict the results of the first 16 games only, based on the long-run trend (which I’ll tediously repeat, is estimated using our model and the available data, covering a relatively long time horizon) and the current level of form/strength (estimated from a combination of data from the bookies).
2. As the games are actually played and the realised results observed, we will be able to assess the performance of the model. More importantly, we will be able to update the form/strength variables from the current value (before the games are played) to a new value, which accounts for how well the first game went. In doing this, we’ll account for how likely each result is predicted to be; for example (see below), Brazil are predicted to beat Croatia quite easily in the opening game. So if indeed they win, this should increase Brazil form/strength, but not by a massive amount, since this is just what we expected them to do. But if, on the other hand, Croatia won that game, then this should impact much more on both teams updated level of form (which in turn will impact on how they approach the next game).
3. Once the form variable has been updated, we will re-run our model adding the 16 observed results and use them to predict the next 16 (round 2 of the first stage).
4. Repeat steps 2-3 for the third round of the first stage.

Here are the predictions for the first batch of games.

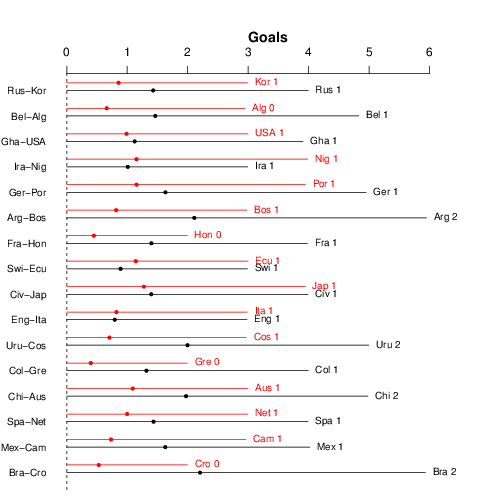
The graph shows the distribution of the predicted number of goals scored by each team in each of the games. The dots indicate the means, while the lines are the 95% interval estimations. In the graph, we also report the median number of goals (_eg _the mean number of goals that Brazil are expected to score against Croatia is slightly over 2, as represented by the black dot on the bottom part of the graph, but the median is exactly 2 goals, as suggested by the text on the bottom-right corner).

The further apart the two strings of text reporting the label for the teams and the predicted median number of goals, the wider the difference between them (and so the more clear-cut the game, in terms of the prediction). I think the most interesting game is England-Italy (you probably think I would say that regardless, but I mean: look at the graph!); while Italy seem to have a tiny advantage in terms of the mean, the two distributions are effectively identical \(-\) a very, very close game, on paper. Ecuador-Switzerland is pretty close too, but the South Americans seem to have a slightly higher mean.

In a sense, more of the same, if you look at the probability distributions for the three outcomes (team 1 win, team 2 win or they draw); again England-Italy is basically a Uniform distribution, while more or less, most of the other games show more unbalanced situations, with one of the two teams having a substantial higher probability of winning than their opponent.

Of course, we won’t take responsibility for any money you will lose by betting on the games, based on our results!