When the going gets tough…
Getting closer to my personal Euro2012 derby: England v Italy.
I find amusing that both sets of media think that their respective team have been gifted a good tie. The English are very happy to have avoided Spain, while the Italians don’t mind not playing the French. I guess these both make sense (particularly for the Italians, it is always very tense when we play France and I suppose we do mind the thought of getting kicked out by them).
But: may be there’s something quite not adding up when both sides think they are favorite and that it is their turn to shine and go through to the semis. I really think it’s a very close game and my subjective prior for the game is genuinely vague. Here’s how I would proceed to formalise it.
First I would look for “hard” evidence to inform my thought process: Italy have played England 23 times; we have won more games (9 to 7) but overall have a worse goal difference (26 for and 28 against). In the last 15 years, we’ve played each other only 5 times. In the two official games Italy won one (at Wembley) and drew one. Italy also won two of the friendly games, while England won the remaining one. The last of those occasions was in 2002 and Buffon is the only player to still be around (as an active footballer, that is). So, I think all in all these stats are not very helpful to inform a prior distribution.
Then I would look for info on more recent games, even if not head-to-head. The graph below shows the recent form of the two teams (in every game they played in 2011/2012, including the first games in the Euro2012).

Looks like England are doing a bit better of late. However, the last three (competing) games were against:
- a very good opponent (Spain and France for Italy and England, respectively);
- a good and a so-so opponent (Croatia and Sweden); and
- a so-so and a good opponent (Ireland and Ukraine). So, the difference in form seems to be in the fact that all other things equal (well, not really, but you know what I mean…) England managed to get a scruffy win aganist Ukraine, while Italy failed to hold on long enough and conceded an equaliser to Croatia. On the other hand, England have not succeeded in winning 3 games in a row in the last year. Again, probably not too much to go about to distinguish among the teams.
So, one way to form a prior is the following. Assume that I’m willing to consider a convenient parametric distribution for \(\theta\), the probability that Italy win the game. For example, I can consider \(\theta \sim \mbox{Beta}(\alpha,\beta)\). [As usual, this is just one of the possible forms for the prior; there’s nothing special about it, if not its mathematical properties!]
Now, consider these three quantities:
- the (assumed, by me) mode of the distribution. Given all the uncertainty, which I was not able to resolve by looking at existing data, I’ll assume this to be 0.5, meaning that I am really very uncertain about who’s going to win and think that the best bet is 50:50.
- The (assumed, by me) upper level of probability that I can consider as reasonable to represent the chance that Italy win the game. Of course, I don’t think that there is absolute certainty that Italy will go through, so this level will be less than 1. I think I would go as far as to \(u=\).8.
- The (assumed, by me) cumulative probability that \(\theta<u\). This gives an indication of the uncertainty that I’m placing over this distribution, while imposing some mathematical constraints on it. For example, because I’m assuming that \(u=\).8 and that mode$=$0.5, this cumulative probability should be relatively large. I feel confident that this would be a reasonable upper limit, and thus I consider $p=(<u)=$0.85.
With these values and using some reasonably simple code (optimising the values of the parameters \(\alpha,\beta\) to meet the constraints just imposed \(-\) discussed here), I can derive that my choice is equivalent to considering $==$3.2618. This is my resulting prior.
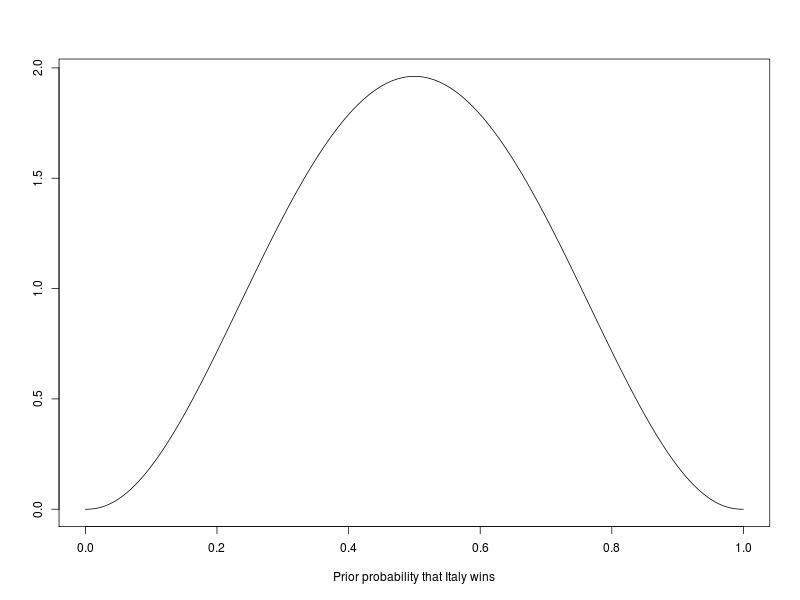
Not very informative \(-\) in fact almost at all. I’m saying that in my view, before the game starts and having observed the relevant evidence available to me up to now, my assessment of the probability that Italy beat England is somewhere in between 15% and 85%. Still, just a bit better than a standard “minimally informative” prior, eg Beta(0.5,0.5). More importantly, it forces you (or me, in this case) to think of the consequences of the choice in terms of the probabilities that are induced by this choice.
Estimating the predictive distribution of the result is the actual objective of the exercise. In fact, I’m not really interested in \(\theta\). Given this (prior) information, a large number of simulations produces a median value of 1, which means that I’m predicting Italy to win \(-\) but with a huge uncertainty attached.