5. Network meta analysis


Gianluca Baio

Department of Statistical Science   |   University College London

g.baio@ucl.ac.uk


https://gianluca.statistica.it

https://egon.stats.ucl.ac.uk/research/statistics-health-economics

https://github.com/giabaio   https://github.com/StatisticsHealthEconomics  

@gianlubaio@mas.to     @gianlubaio    


Bayesian modelling for economic evaluation of healthcare interventions

València International Bayesian Analysis Summer School, 7th edition, University of Valencia

10 - 11 July 2024

Check out our departmental podcast “Random Talks” on Soundcloud!

Follow our departmental social media accounts + magazine “Sample Space”

Summary

  • Motivation for Network Meta Analysis (NMA)

    • Example: Smoking cessation

  • Fixed effects meta-analysis

  • Random effects meta-analysis

References

Multiparameter evidence synthesis

Introduction

  • Unusual for a policy question to be informed by a single study
    • Must use all available and relevant evidence
  • Multiparameter evidence synthesis
    • Learning about more than one quantity from combination of direct and indirect evidence
    • Example: Network Meta Analysis (NMA)

Network Meta Analysis

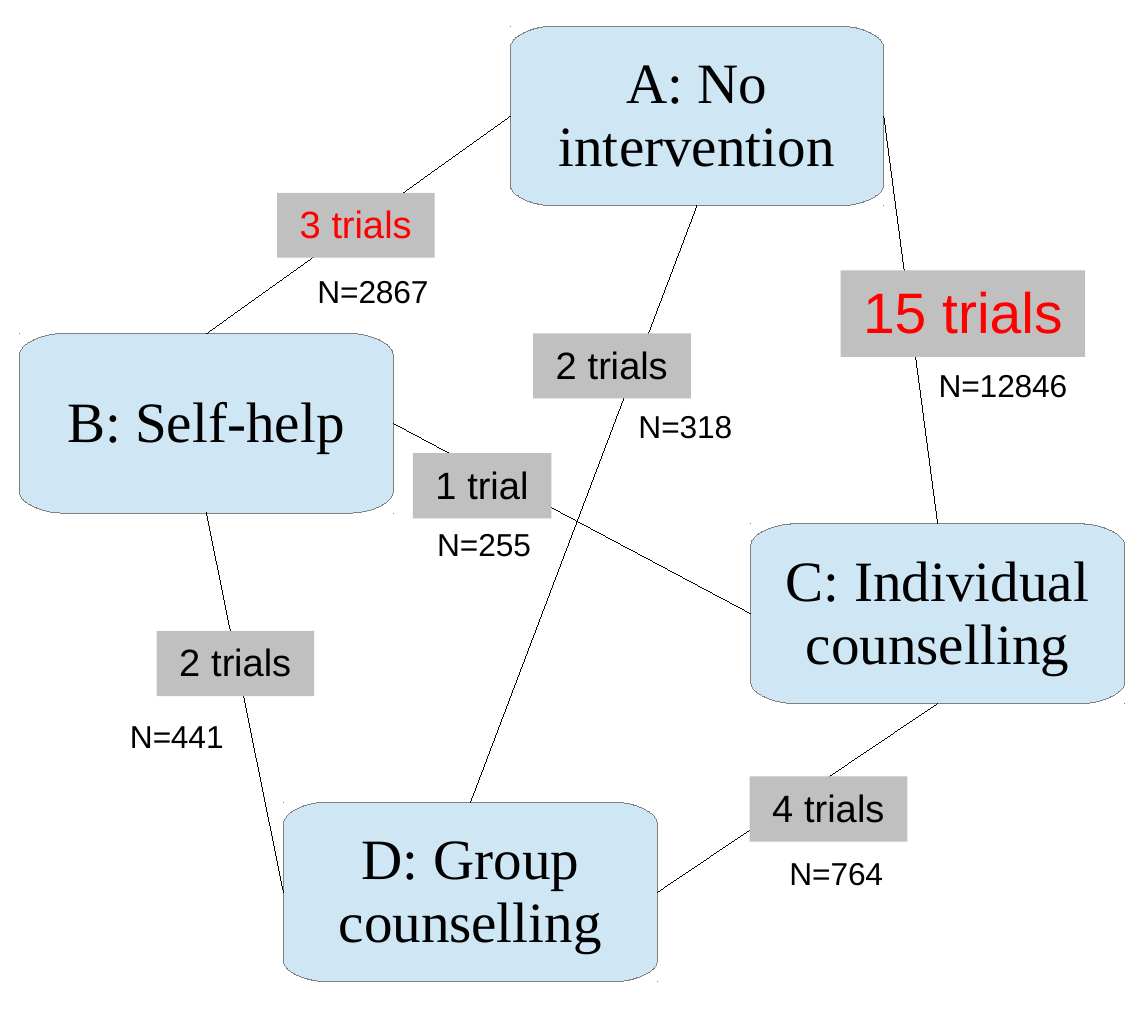
Simplest example

  • New treatment C: been trialled against old treatment B, but not to A

  • For health economic evaluation need to compare A/B/C together

  • Learn about C/A effect from C/B and B/A trial data

  • Also called “mixed treatment comparisons”
    • Since can also “mix” direct and indirect data on same comparison…

Common in UK health technology assessment, but require some statistical skills!

Smoking cessation trial

Data

Comparison A: No intervention B: Self-help C: Individual counselling D: Group counselling
AB 79 / 702 77 / 694
18 / 671 21 / 535
8 / 116 19 / 149
AC 75 / 731 363 / 714
2 / 106 9 / 205
58 / 549 237 / 1561
0 / 33 9 / 48
3 / 100 31 / 98
1 / 31 26 / 95
6 / 39 17 / 77
64 / 642 107 / 761
5 / 62 8 / 90
20 / 234 34 / 237
95 / 1107 143 / 1031
15 / 187 36 / 504
78 / 584 73 / 675
69 / 1177 54 / 888
ACD 9 / 140 23 / 140 10 / 138
AD 0 / 20 9 / 20
BC 20 / 49 16 / 43
BCD 11 / 78 12 / 85 29 / 170
BD 7 / 66 32 / 127
CD 12 / 76 20 / 74
9 / 55 3 / 26

Outcome

  • Successfully quit smoking by 6-12 months

  • Number of success / number of participants

Set up

  • 24 trials in total

  • Network of comparisons involving 4 interventions

  • Not all interventions tested against all others!

Objective

  • Estimate the overall effectiveness of the interventions

  • Potentially add cost-effectiveness analysis

Smoking cessation trial

Network of comparisons

  • All comparisons have at least one trial with direct data

  • We wish to enhance direct with indirect evidence

  • e.g. A-D comparison (only 2 direct trials) improved by including A-C, C-D trials (15 + 4)

In general…

Network of comparisons

  • In other applications, might want to learn about comparisons with no direct trial evidence

  • e.g. how much better than current treatment C is new treatment D?

“Fixed effects” NMA

  • Log odds of response in each arm modelled as effect of study \(\class{red}{s}\) plus effect of treatment \(\class{red}{t}\) \((s = 1, \ldots , NS\), different values of \(t\) in each \(s)\)

\[\begin{align} & \class{myblue}{r_{st}} \class{myblue}{\sim} \class{myblue}{\dbin(p_{st},n_{st})} \\ & \class{myblue}{\logit(p_{st})} \class{myblue}{=}\class{myblue}{\mu_s + \delta_{st}} \\ & \class{myblue}{\delta_{st}}\class{myblue}{=} \class{myblue}{d_t - d_{t_{s0}}} \end{align}\]

  • Study effects \(\mu_s\): log odds in baseline group of study \(s\), considered independent between studies

  • Treatment effects

    \(\delta_{st}\): compared to study \(\class{red}{s}\) baseline \(t_{s_{s0}}\)
    \(d_t\): compared to overall baseline treatment \(t=1\) (e.g. placebo) \(\Rightarrow d_1 :=0\) - This essentially means that the effect of treatment \(t=1\) versus the effect of the baseline treatment (again \(t=1\)) is… nothing \((=0)\)!

  • “Fixed” effects: \(d_t\) are identical in each study \(s\)

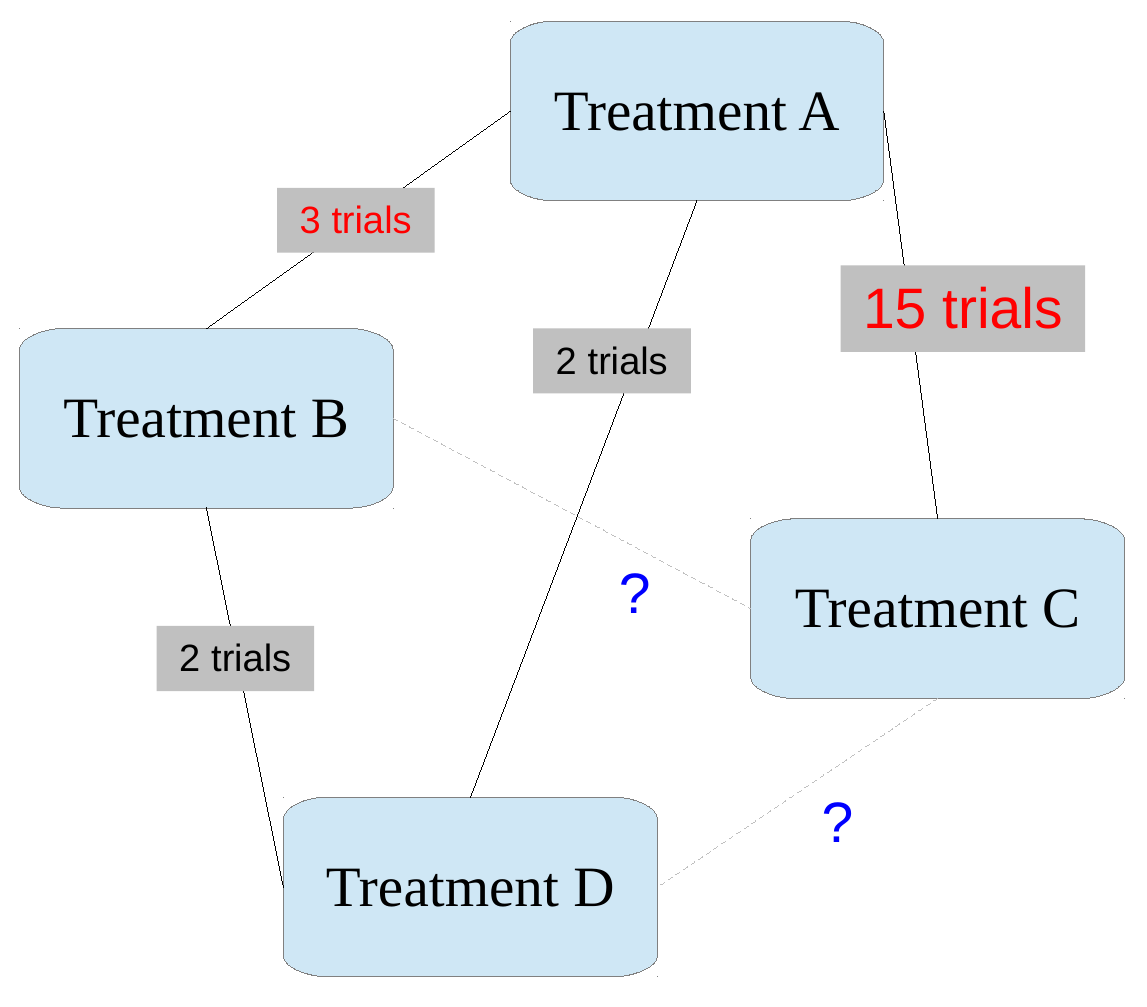
Estimating effects of indirect comparisons

Smoking cessation example

  • \(\log \OR\)s \(d_B\), \(d_C\), \(d_D\) (compared to “baseline” treatment A) are directly identifiable from A-B, A-C, A-D trials

But: can deduce indirect comparisons from these basic parameters (with assumptions…)

  • \(\log\OR\) of C compared to B is \(d_C-d_B\)
  • \(\log\OR\) of D compared to B is \(d_D-d_B\)
  • \(\log\OR\) of D compared to D is \(d_D-d_C\)

NB This assumes consistency between indirect and (potential) direct evidence!

  • Consider \(t=B\)
  • By definition: \(\logit(p_{st}) = \log\left(\frac{p_{st}}{1-p_{st}}\right) =\log\) odds of the event (quit smoking), if you are in group B
  • Similarly, \(\logit(p_{sA}) = \log\left(\frac{p_{sA}}{1-p_{sA}}\right) =\log\) odds of the event (quit smoking), if you are in group A \((\Rightarrow t=1)\)
  • By definition: \(\displaystyle \OR_{BA}=\frac{\style{font-family:inherit;}{\text{odds}}_B}{\style{font-family:inherit;}{\text{odds}}_A} \Rightarrow \log\OR_{BA}= \log\ \style{font-family:inherit;}{\text{odds}}_B - \log\ \style{font-family:inherit;}{\text{odds}}_A = \logit(p_{sB})-\logit(p_{sA})\)
  • So \[\begin{align} \log\OR_{BA} &= \logit(p_{sB})-\logit(p_{sA}) \\ &= \left[\mu_s + \delta_{sB} \right] - \left[\mu_s + \delta_{sA} \right] \\ &= \left[\mu_s +(d_B - d_A)\right] -\left[\mu_s +(d_A - d_A)\right] \\ &= d_B -d_A \\ &= d_B \qquad (\style{font-family:inherit;}{\text{because }} d_A=d_1:=0) \end{align}\]

Manipulating data

Nested indices

# Shows the first 2 rows...
head(smoke.list$r,2)
     [,1] [,2] [,3] [,4]
[1,]   79   77   NA   NA
[2,]   18   21   NA   NA
# ...and the last 4 rows of the data for the number of quitters in each arm
tail(smoke.list$r,4)
      [,1] [,2] [,3] [,4]
[21,]   NA   11   12   29
[22,]   NA    7   NA   32
[23,]   NA   NA   12   20
[24,]   NA   NA    9    3
# In study 1, treatments 3 (=C) and 4 (=D) are not present so the data show 'NA'
# Similarly, in study 21, treatment 1 (=A) was not involved, so there's a 'NA'
# Similarly, shows the first 2 rows...
head(smoke.list$n,2) 
     [,1] [,2] [,3] [,4]
[1,]  702  694   NA   NA
[2,]  671  535   NA   NA
# ...and the last 4 rows of the data for the total sample size in each arm
tail(smoke.list$n,4)
      [,1] [,2] [,3] [,4]
[21,]   NA   78   85  170
[22,]   NA   66   NA  127
[23,]   NA   NA   76   74
[24,]   NA   NA   55   26
# Here shows the first 2 and last 4 rows of the matrix indicating the treatment included in the comparison
head(smoke.list$t,2)
     t1 t2 t3
[1,]  1  2 NA
[2,]  1  2 NA
tail(smoke.list$t,4)
      t1 t2 t3
[21,]  2  3  4
[22,]  2  4 NA
[23,]  3  4 NA
[24,]  3  4 NA
# So in study number 1, the comparison is between intervention 1 (=A) and intervention 2 (=B)
# while in study number 21, the comparison is among interventions 2 (=B), 3 (=C) and 4(=D)
# What are the treatment involved in study 21?
smoke.list$t[21,]
t1 t2 t3 
 2  3  4 
# What is the number of quitters in study 21 and in the second treatment arm of that study?
smoke.list$r[21,smoke.list$t[21,2]]
[1] 12
# What is the sample size in study 21 and in the second treatment arm of that study?
smoke.list$n[21,smoke.list$t[21,2]]
[1] 85

Coding NMA in BUGS/JAGS

Just write out the equations-ish… 😉

  • NB: t[s,a] indicates the treatment associated with study s and its arm a

  • Vague priors for effects / baseline are typically OK

    • But not when the number of comparisons is very small!
for(s in 1:NS) {
  for (a in 1:na[s])  {
    r[s,t[s,a]] ~ dbin(p[s,t[s,a]], n[s,t[s,a]])
    logit(p[s,t[s,a]]) <- mu[s] + delta[s,t[s,a]]
  }
# delta are effects compared to arm 1 of each study s
  delta[s,t[s,1]] <- 0
  for (a in 2:na[s])  {
    delta[s,t[s,a]] <- d[t[s,a]] - d[t[s,1]]
  }
}
for (i in 1:NS){
# vague prior for baseline log-odds
  mu[i] ~ dnorm(0,0.0001) 
}
# effect compared to treatment 1 (e.g. placebo)
d[1] <- 0  
# vague prior
for (i in 2:NT) {  
  d[i] ~ dnorm(0, 0.0001)  
}

Presenting treatment effects

For each treatment \(2, \ldots, NT\) compared to treatment 1 (the reference/baseline: eg “no intervention”/“status quo”, or placebo), can back-transform the \(\log\OR\)s

for (t in 2:NT) {
  or[t] <- exp(d[t])  # odds ratios
}

Then can compute the odds ratio for every other treatment pair c, k – even if no direct comparison exist

  • \(\OR_{ck} = \OR_{c1} / \OR_{k1}\)
for (c in 1:(NT-1)) {
  for (k in (c+1):NT) {
    or[c,k] <- exp(d[c] - d[k])
    or[k,c] <- 1/or[c,k]
  }
}

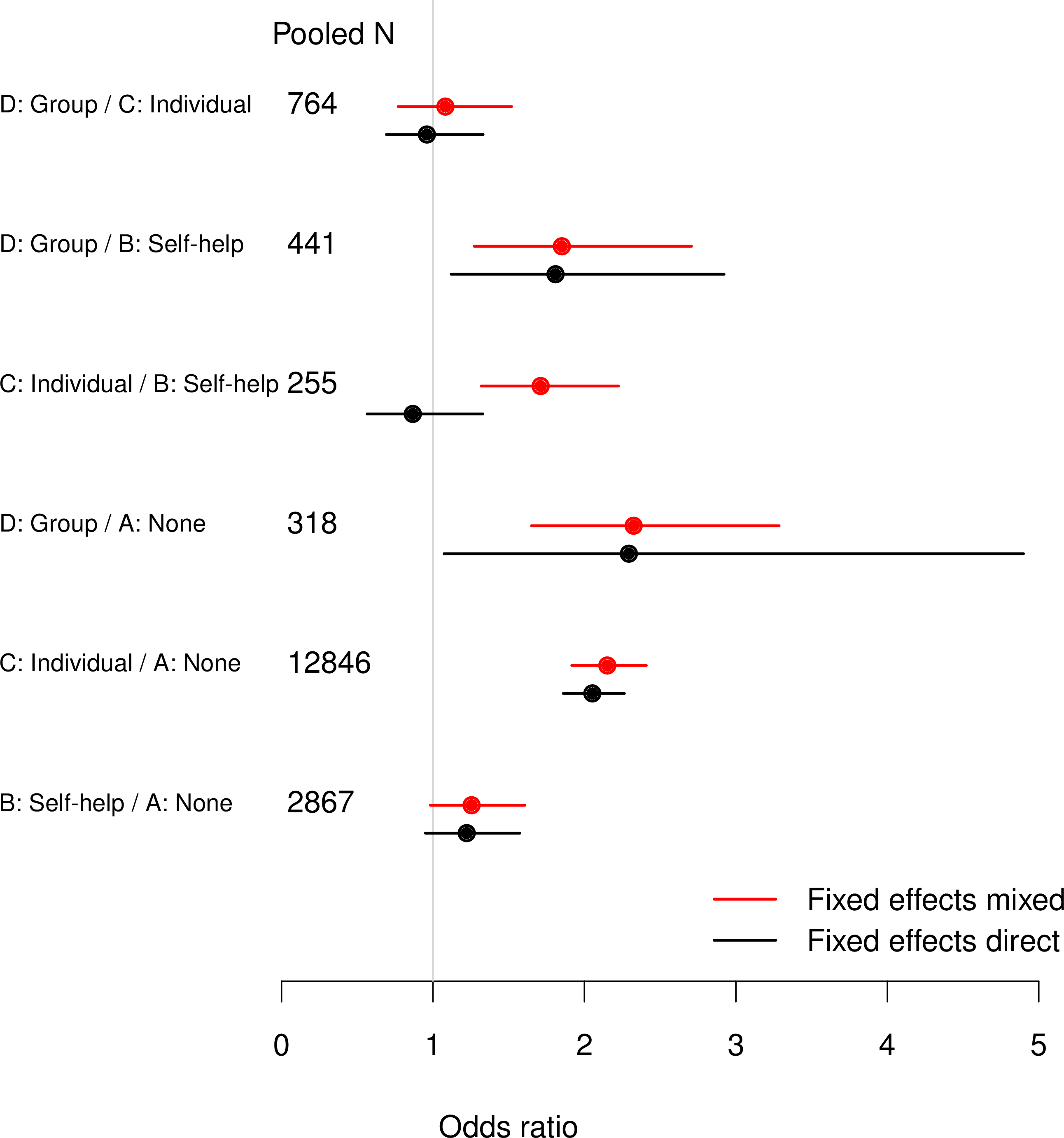
Results

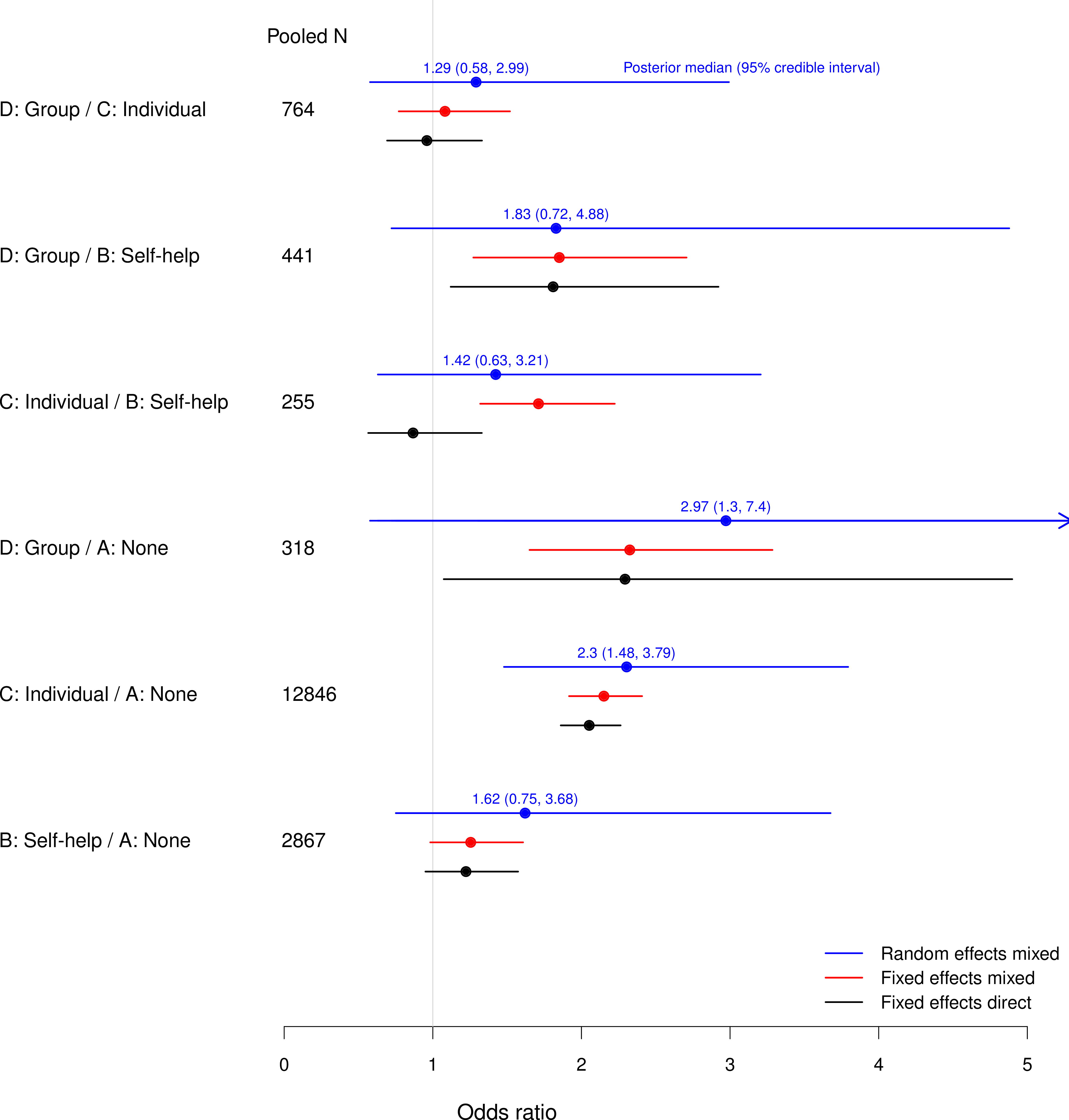
Comparing direct and mixed evidence

Direct-only odds ratios (CIs) from classical analysis of pooled individual data

  • Precision of D/A estimate improved by indirect C/A and C/D data

  • Strong direct data for other comparisons, so not improved much by indirect evidence

  • C/B estimate from one direct study \(\Rightarrow\) pulled towards much bigger indirect C/A and B/A data

    • evidence of heterogeneity…

Results

Heterogeneity between individual studies

  • Classical odds ratio (CIs) for all individual trials, sorted by pairwise comparison

  • Heterogeneity between ORs within most comparisons

  • Consider “random” effects models…

Random effects NMA

Replace fixed effects \(\delta_{st}\) of treatment \(t\) in study \(s\)

\[\begin{align} & \class{myblue}{r_{st}} \class{myblue}{\sim} \class{myblue}{\dbin(p_{st},n_{st})} \\ & \class{myblue}{\logit(p_{st})} \class{myblue}{=}\class{myblue}{\mu_s + \delta_{st}} \\ & \class{myblue}{\delta_{st}}\class{myblue}{=} \class{myblue}{d_t - d_{t_{s0}}} \end{align}\]

with a .red[random effect] varying between studies \(s\) with a Normal distribution with mean defined by the fixed effect \[\begin{align} & \class{myblue}{r_{st}} \class{myblue}{\sim} \class{myblue}{\dbin(p_{st},n_{st})} \\ & \class{myblue}{\logit(p_{st})} \class{myblue}{=}\class{myblue}{\mu_s + \delta_{st}} \\ & \class{myblue}{\delta_{st}\sim\dnorm(\mu_{st}^\delta, \sigma^2_{st})} \\ & \class{myblue}{\mu_{st}^\delta}\class{myblue}{=} \class{myblue}{d_t - d_{t_{s0}}} \end{align}\]

still with \(\delta_{st}=0\) for \(t=\) baseline arm of \(s\)

Coding this in BUGS/JAGS

Equations translate relatively straight to BUGS model, again:

for (a in 2:na[s]) {
  delta[s,t[s,a]] <- d[t[s,a]] - d[t[s,1]]
}

is replaced by:

for (a in 2:na[s]) {
  delta[s,t[s,a]] ~ dnorm(md[s,t[s,a]], taud[s,t[s,a]])
  md[s,t[s,a]] <- d[t[s,a]] - d[t[s,1]]
  taud[s,t[s,a]] <- tau
}
d[1] <- 0  
# Priors on the mean same as fixed effects
for (i in 2:NT) {
  d[i] ~ dnorm(0, 0.0001) 
}

But: a couple of complicating features…

Constraints on random effects variances

  • In a NMA, we have
    • \(NT\) different treatments
    • \((NT - 1)\) different pooled effects, relative to treatment 1 (the baseline / reference) Only 1 effect in standard meta-analysis
  • \((NT-1)\) different random effects distributions to estimate?
    • Not feasible unless many studies of every single treatment
    • \(\Rightarrow\) identifiability constraints needed
  • Assume same random effects variance for each treatment comparison

Prior for \(\class{red}{\sigma^2}\): Uniform from 0 to a large upper limit (eg 10 if on the log scale) is often used, especially to align with standard meta-analysis

  • But: Beware of sensitivity to this — particularly if only few studies are considered…

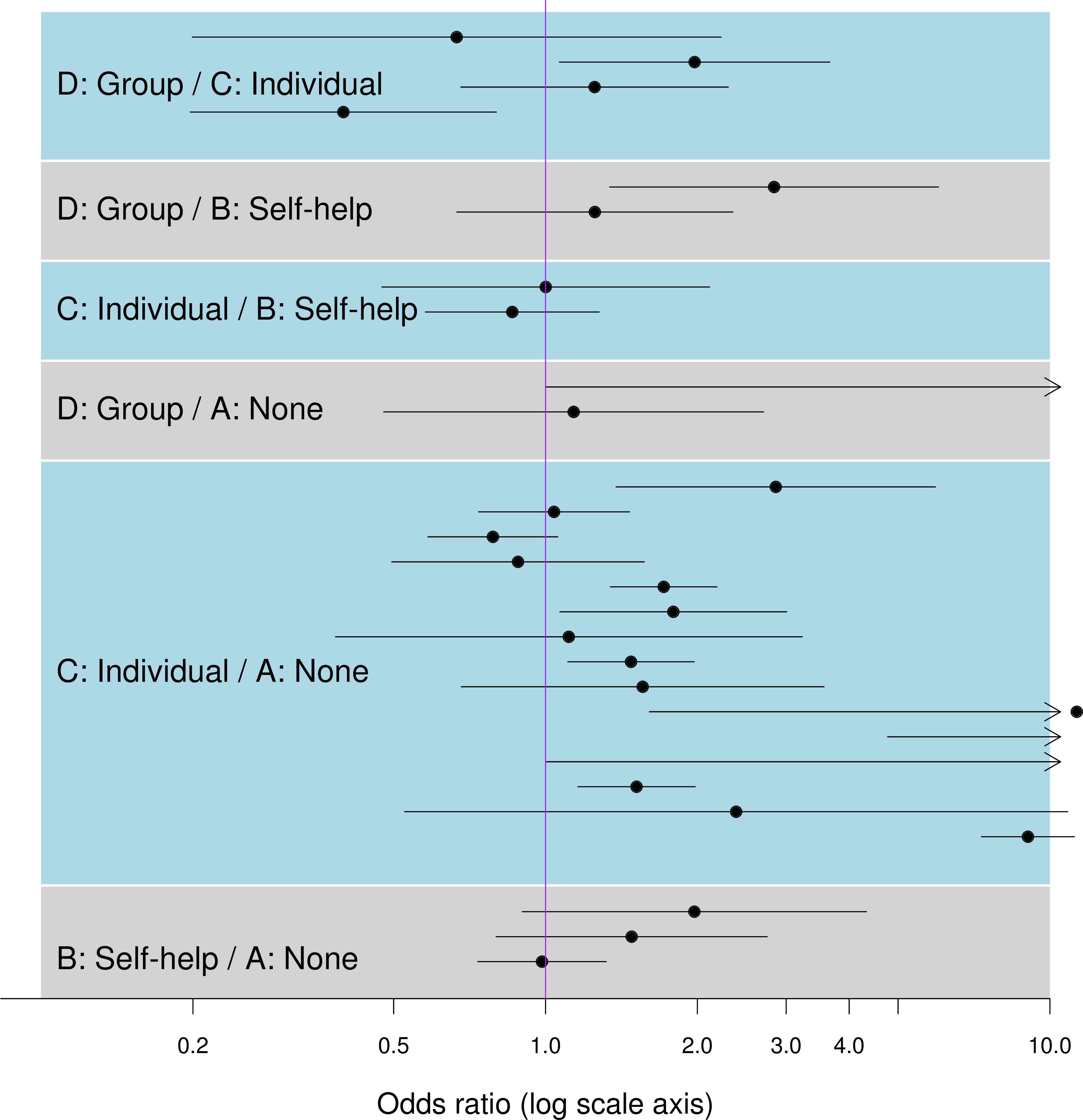
Results

Random effects models

  • Wider CIs after accounting for heterogeneity

  • C/B: compromise between direct and indirect evidence

  • D/A: smallest trials, still a lot of uncertainty

Use in cost-effectiveness analysis

Example

External data on Expected Life-Years Gained if quit smoking:

  • around 15 years (sd \(\approx\) 4): model as \(L\sim \dnorm(\style{font-family:inherit;}{\text{mean}} =15,\style{font-family:inherit;}{\text{sd}}=4)\)

  • and code this as L ~ dnorm(15, 0.0625) in BUGS

Model \(L\) by Prob(quit) to get E[LYG] under each intervention

and compare to cost of each intervention:

Further issues…

  • Different type of outcomes

    • Binary data (Binomial models, as here)
    • Counts of events/person-years at risk (Poisson models)
    • Mean + sd of continuous outcomes (Normal models) … in each arm of the study

  • Individual patient data alongside data aggregated by arms

  • Meta-regression: explain heterogeneity between studies using study-level characteristics as covariates

  • Detecting / handling conflicts between direct / indirect evidence

Further tools

GeMTC

nmaINLA

multinma Slides

1. Intro HTA 2. Bayesian computation 3. ILD 4. ALD 5. NMA   © Gianluca Baio (UCL)   |             |   Bayesian models in HTA   |   VIBASS7 2024   |   10 - 11 July 2024   |