model { for (i in 1:N) { y[i] ~ dnorm(mu[i], tau) mu[i] <- alpha + beta*x[i] } tau ~ dgamma(0.1,0.1) sigma <- pow(tau,-0.5) alpha ~ dnorm(0,0.01) beta ~ dnorm(0,0.01) }model { for (i in 1:N) { y[i] ~ dnorm(mu[i], tau) mu[i] <- alpha + beta*x[i] } tau ~ dgamma(0.1,0.1) sigma <- pow(tau,-0.5) alpha ~ dnorm(0,0.01) beta ~ dnorm(0,0.01) }model { for (i in 1:N) { y[i] ~ dnorm(mu[i], tau) mu[i] <- alpha + beta*x[i] } tau ~ dgamma(0.1,0.1) sigma <- pow(tau,-0.5) alpha ~ dnorm(0,0.01) beta ~ dnorm(0,0.01) }model { for (i in 1:N) { y[i] ~ dnorm(mu[i], tau) mu[i] <- alpha + beta*x[i] } tau ~ dgamma(0.1,0.1) sigma <- pow(tau,-0.5) alpha ~ dnorm(0,0.01) beta ~ dnorm(0,0.01) }
2. Bayesian computation
Gianluca Baio
Department of Statistical Science | University College London
https://gianluca.statistica.it
https://egon.stats.ucl.ac.uk/research/statistics-health-economics
https://github.com/giabaio https://github.com/StatisticsHealthEconomics
@gianlubaio@mas.to @gianlubaio
Bayesian modelling for economic evaluation of healthcare interventions
València International Bayesian Analysis Summer School, 7th edition, University of Valencia
10 - 11 July 2024
Check out our departmental podcast “Random Talks” on Soundcloud!
Follow our departmental social media accounts + magazine “Sample Space”
Bayesian computation
- Forward sampling (Monte Carlo)
- Express current knowledge as parameters with distributions
- Simulate parameters, make predictions from models based on the parameters
- Like a spreadsheet with randomness on cells. Familiar in health economics as “probabilistic sensitivity analysis”
- Doesn’t really need specialised software
- Learning from data (model fitting)
- Compute posterior distributions combining prior and data, through Bayes’ theorem
- Simpler models — do not require specialised software
- “Vague” priors
- “Conjugate” analysis
- Realistic models — MCMC
- eg: Gibbs sampling
Bayesian computation
Generally speaking, the computational effort depends in large part on the definition of the prior…
- Uniform prior p(θ∣y)=p(θ)p(y∣θ)p(y)∝cL(θ∣y)c∫L(θ∣y)dθ∝L(θ∣y)∫L(θ∣y)dθ
- Conjugate prior p(θ)∈f(θ;a)⇒p(θ∣y)∝p(θ)L(θ∣y)∈f(θ;a∗)
- All other (real-life) cases…
- Can write algorithms to simulate from an unknown target (posterior) distribution
- General-purpose software to deal with all cases…
BUGS/JAGS/Stan/NimbleINLA
General software for Bayesian computation
Different versions of BUGS
WinBUGS1.4.3- Original release 1997 — runs only on
Windows - Stable but no longer developed (latest release: August 2007)
- Freely available from http://www.mrc-bsu.cam.ac.uk/bugs
- Original release 1997 — runs only on
OpenBUGShttp://www.openbugs.net- Open-source offshoot, also runs on
LinuxandMacOS - Works just as well, stable
- Open-source offshoot, also runs on
“Rivals”/alternatives
JAGShttp://mcmc-jags.sourceforge.net- Language essentially identical, Work just as well, stable
- Runs natively on
Mac/Unix/Windows
Stanhttp://mc-stan.org/- Probabilistic language — slightly different than
BUGS/JAGS - Based on different algorithm — can be more efficient in some cases
- Probabilistic language — slightly different than
Interfaces exist to run these from other software, eg (R2OpenBUGS, R2jags, rstan) Excel, S-Plus, SAS, Matlab, Stata, …
BUGS/JAGS
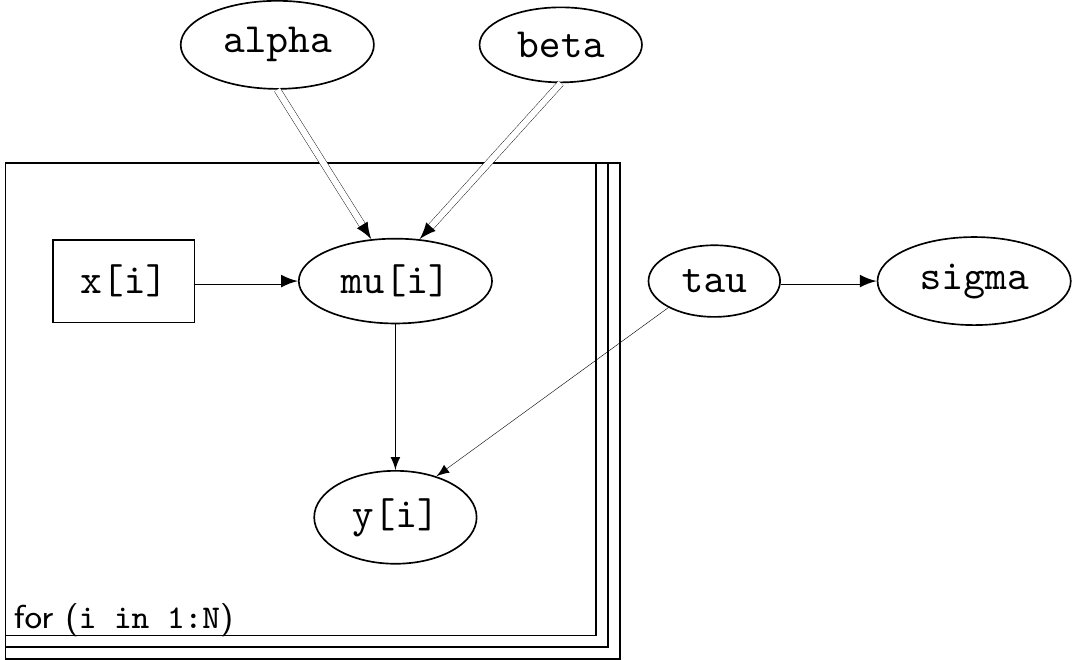
- Language for specifying Bayesian models as a network of known and unknown quantities
Example: linear regression
yi∼Normal(μi,σ)for i=1,…,Nμi=α+βxiτ∼Gamma(0.01,0.01)σ=τ−0.5α∼Normal(0,0.01)β∼Normal(0,0.01)
BUGS/JAGShave a built-in parser, which inspects the set of declarations and translates them into a DAG- Exploits as much as possible the underlying conditional independence relationships to speed up computation
Example — drug
- Consider a drug to be given for relief of chronic pain
- Experience with similar compounds has suggested that annual response rates between 0.2 and 0.6 could be feasible
- Interpret this as a distribution with mean = 0.4 and standard deviation = 0.1
- Can encode these into a Beta(9.2, 13.8) prior
Example — drug
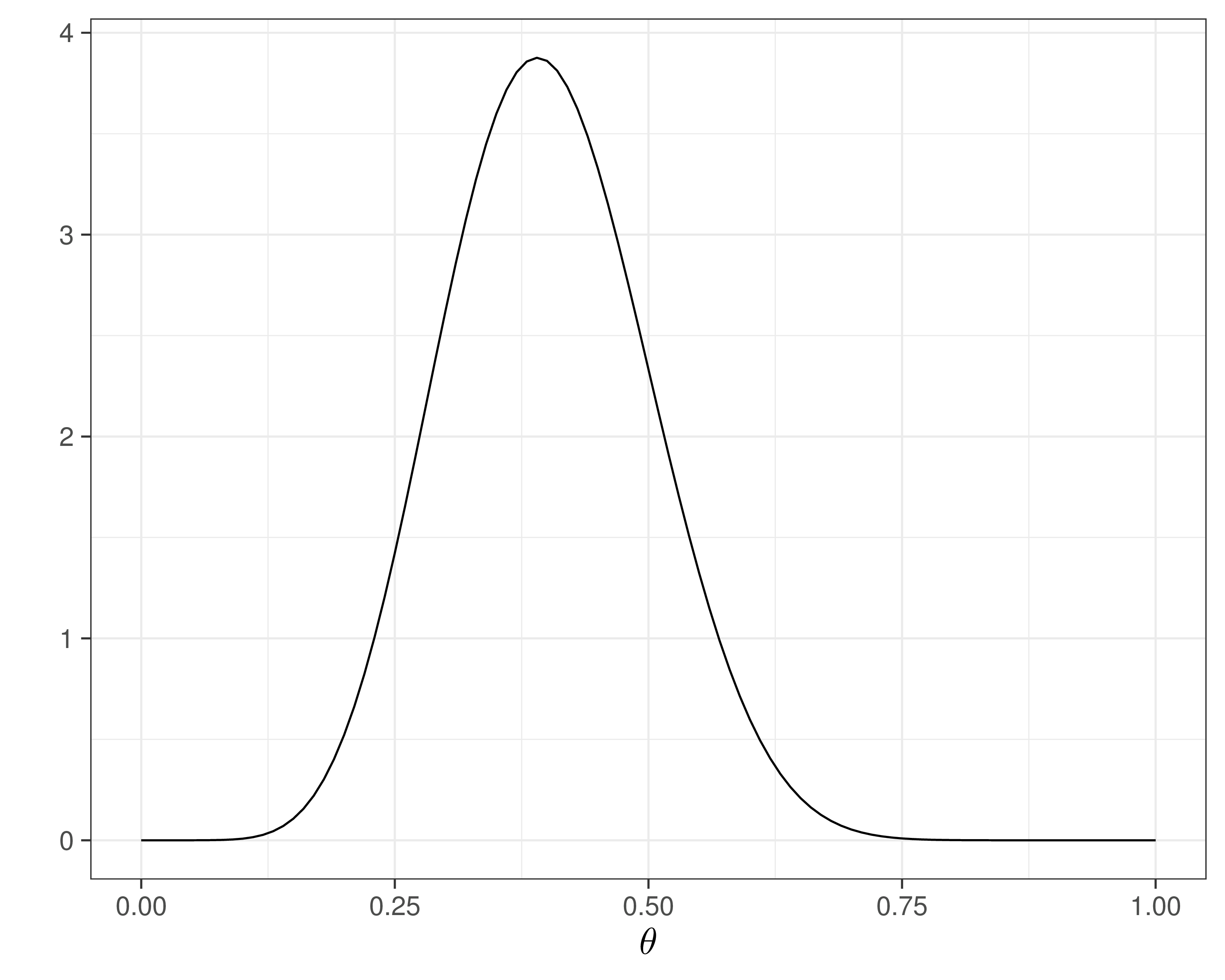
- Suppose we can actually run a small pilot study, in which we observe y=15 in n=20 individuals to whom we give the drug and who are relieved from the back pain
- Update uncertainty over θ = probability of “success” for the drug
- Predict number of successes in the next m=40 patients
- Can model using
y∼Binomial(θ,n)θ∼Beta(a,b)ypred∼Binomial(θ,m)
NB: p(ypred∣y) is the predictive distribution
- Mixes up (revised/posterior) uncertainty in θ and sampling variability (Binomial model)
Running JAGS from R
Map the “pen-and-paper” model into JAGS code
Can code up the model in a
.txt.file
Running JAGS from R
- The object
mcontains the MCMC output
[1] "model" "BUGSoutput" "parameters.to.save"
[4] "model.file" "n.iter" "DIC" - Can explore further and see where various bits are… (but don’t really need to do so…)
[1] "n.chains" "n.iter" "n.burnin" "n.thin"
[5] "n.keep" "n.sims" "sims.array" "sims.list"
[9] "sims.matrix" "summary" "mean" "sd"
[13] "median" "root.short" "long.short" "dimension.short"
[17] "indexes.short" "last.values" "program" "model.file"
[21] "isDIC" "DICbyR" "pV" "DIC"
[25] "time2run" - Can summarise results directly
Inference for Bugs model at "/tmp/RtmpGy2l2J/model22c593971f56c.txt",
2 chains, each with 6000 iterations (first 1000 discarded)
n.sims = 10000 iterations saved. Running time = 0.015 secs
mu.vect sd.vect 2.5% 97.5% Rhat n.eff
theta 0.563 0.076 0.411 0.708 1.001 10000
y.pred 22.491 4.352 14.000 31.000 1.001 10000
deviance 6.660 2.444 3.372 12.683 1.001 10000
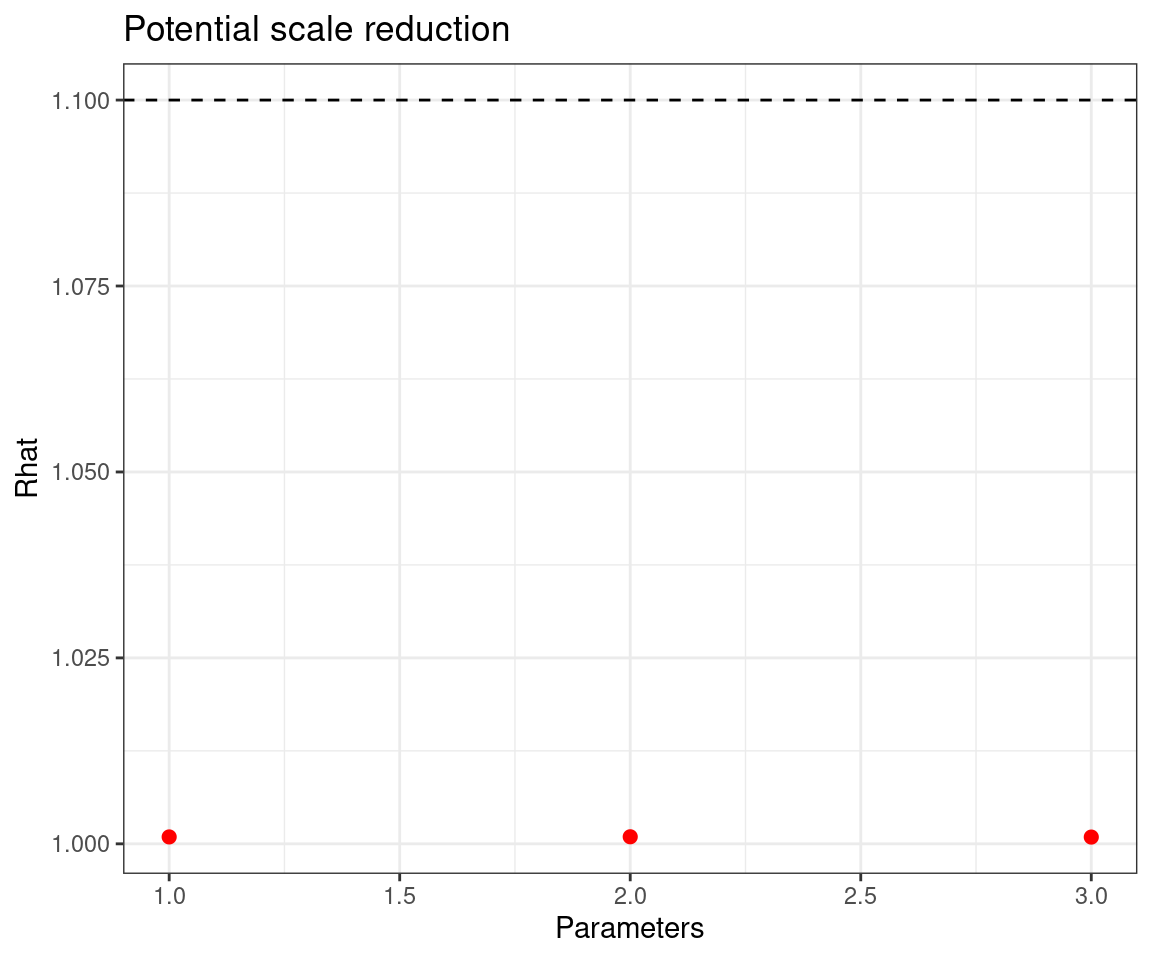
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule: pV = var(deviance)/2)
pV = 3.0 and DIC = 9.6
DIC is an estimate of expected predictive error (lower deviance is better).Post-processing the JAGS output
- We can use directly
Rcode to post-process the results - Or use standardised packages
bmhe(for diagnostics & plots)BCEA(for economic evaluation)- …
# Installs relevant packages # Directly from CRAN (main repository) install.packages("BCEA") install.packages("R2jags") # Or from GitHub (more experimental packages) remotes::install_github("giabaio/bmhe_utils") remotes::install_github("giabaio/R2jags")# Installs relevant packages # Directly from CRAN (main repository) install.packages("BCEA") install.packages("R2jags") # Or from GitHub (more experimental packages) remotes::install_github("giabaio/bmhe_utils") remotes::install_github("giabaio/R2jags")# Installs relevant packages # Directly from CRAN (main repository) install.packages("BCEA") install.packages("R2jags") # Or from GitHub (more experimental packages) remotes::install_github("giabaio/bmhe_utils") remotes::install_github("giabaio/R2jags")
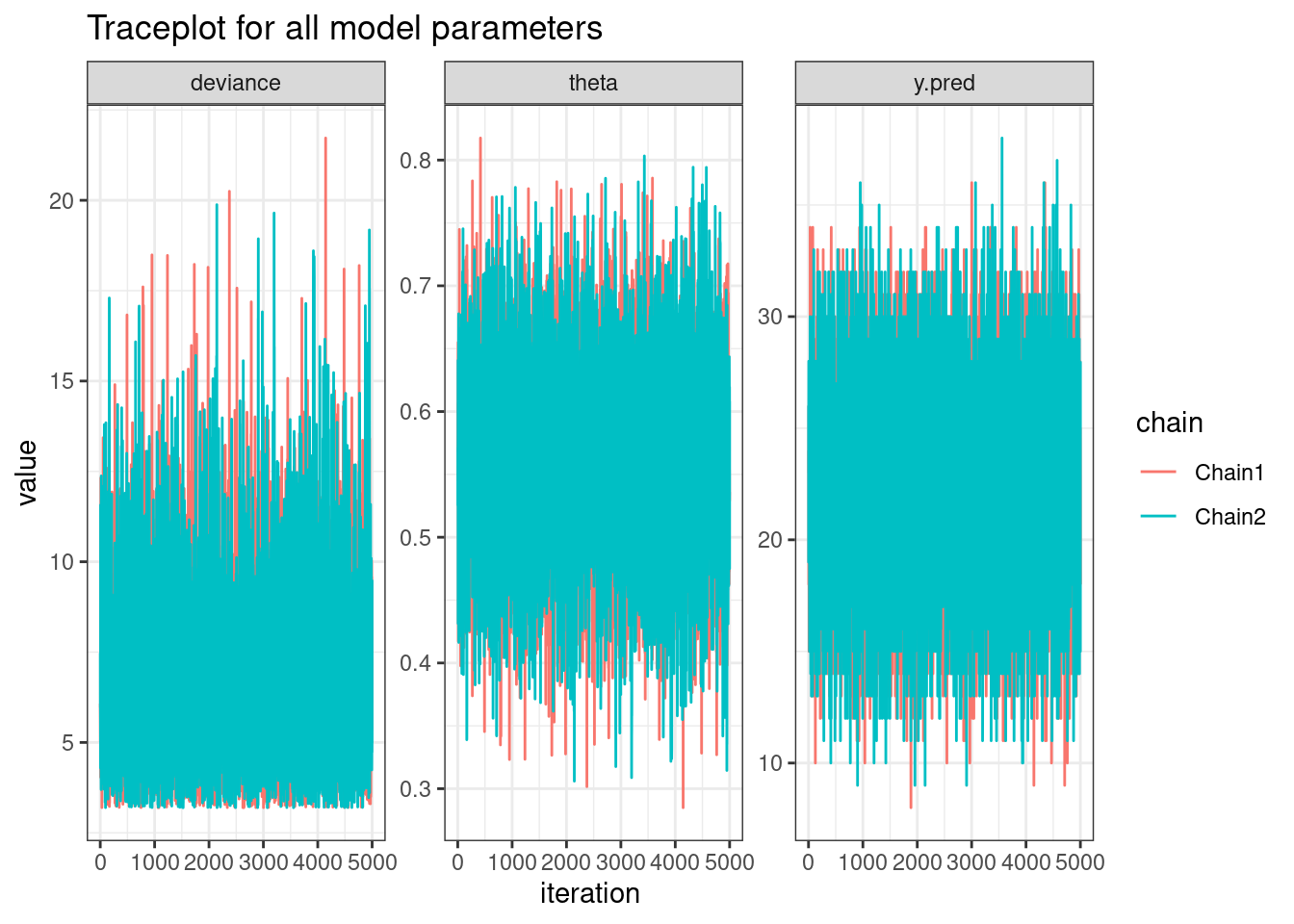
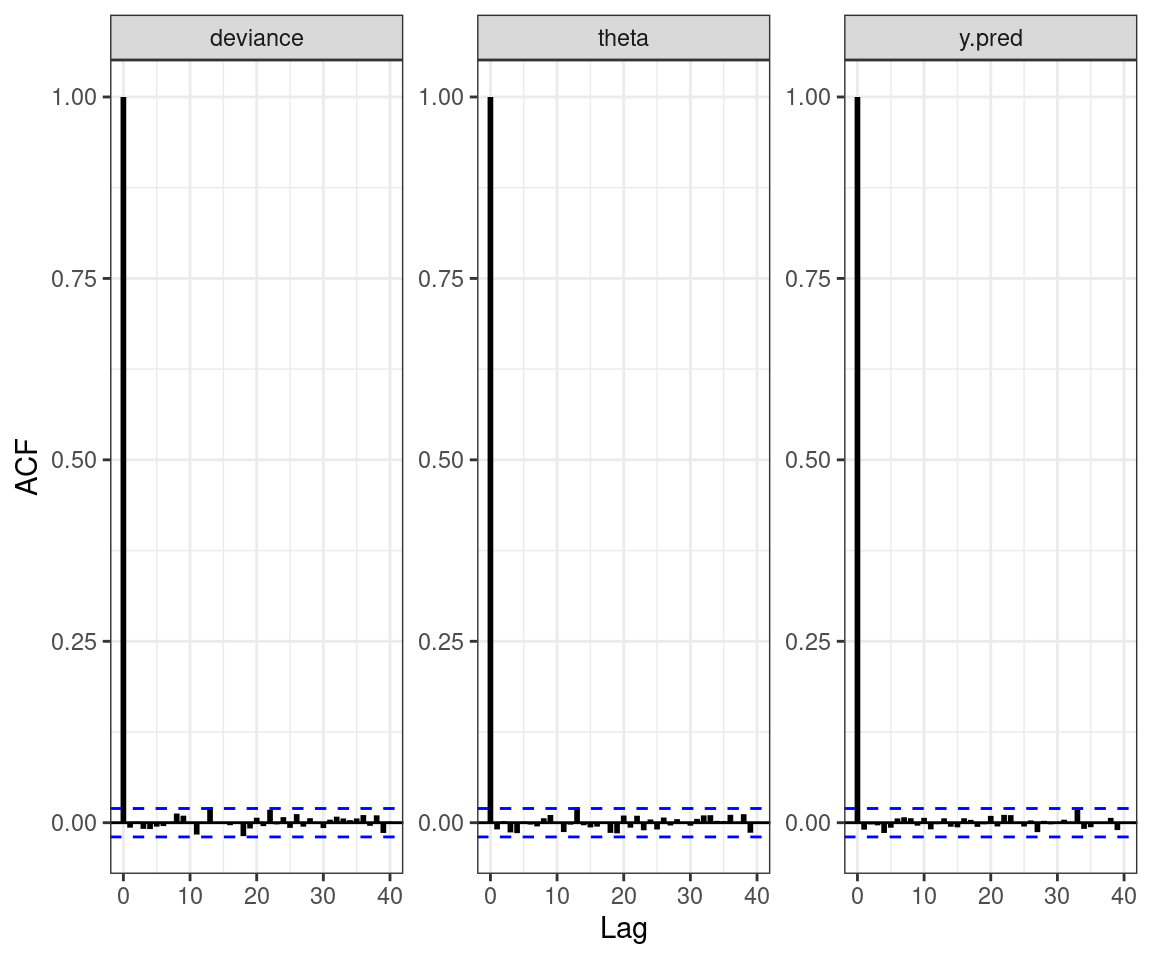
Post-processing the JAGS output
Post-processing the JAGS output
Post-processing the JAGS output
1. Intro HTA 2. Bayesian computation 3. ILD 4. ALD 5. NMA © Gianluca Baio (UCL) | | Bayesian models in HTA | VIBASS7 2024 | 10 - 11 July 2024 |
2. Bayesian computation Gianluca Baio Department of Statistical Science | University College London g.baio@ucl.ac.uk https://gianluca.statistica.it https://egon.stats.ucl.ac.uk/research/statistics-health-economics https://github.com/giabaio https://github.com/StatisticsHealthEconomics @gianlubaio@mas.to @gianlubaio Bayesian modelling for economic evaluation of healthcare interventions València International Bayesian Analysis Summer School, 7th edition, University of Valencia 10 - 11 July 2024 Check out our departmental podcast “Random Talks” on Soundcloud! Follow our departmental social media accounts + magazine “Sample Space”