| ID | Trt | Sex | Age | \(\ldots\) | \(y_0\) | \(\ldots\) | \(y_J\) | \(u_0\) | \(\ldots\) | \(u_J\) | \(c_0\) | \(\ldots\) | \(c_J\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | M | 23 | \(\ldots\) | \(y_{10}\) | \(\ldots\) | \(y_{1J}\) | 0.32 | \(\ldots\) | 0.44 | 103 | \(\ldots\) | 80 |
| 2 | 1 | M | 23 | \(\ldots\) | \(y_{20}\) | \(\ldots\) | \(y_{2J}\) | 0.12 | \(\ldots\) | 0.38 | 1204 | \(\ldots\) | 877 |
| 3 | 2 | F | 19 | \(\ldots\) | \(y_{30}\) | \(\ldots\) | \(y_{3J}\) | 0.49 | \(\ldots\) | 0.88 | 16 | \(\ldots\) | 22 |
| \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) |
3. Individual level data in HTA
Gianluca Baio
Department of Statistical Science | University College London
https://gianluca.statistica.it
https://egon.stats.ucl.ac.uk/research/statistics-health-economics
https://github.com/giabaio https://github.com/StatisticsHealthEconomics
@gianlubaio@mas.to @gianlubaio
Bayesian modelling for economic evaluation of healthcare interventions
València International Bayesian Analysis Summer School, 7th edition, University of Valencia
10 - 11 July 2024
Check out our departmental podcast “Random Talks” on Soundcloud!
Follow our departmental social media accounts + magazine “Sample Space”
Summary
Data & “standard” analysis
Example: 10 Top Tips
Analysis of cost-effectiveness data
- General structure
- Alternative models
Model comparison
References
- Bayesian Methods in Health Economics, chapters 5.1, 5.2
Individual level data
HTA alongside RCTs
- The available data usually look something like this
where
- \(y_{ij}=\) Survival time, event indicator (eg CVD), number of events, continuous measurement (eg blood pressure), …
- \(u_{ij}=\) Utility-based score to value health (eg EQ-5D, SF-36, Hospital & Anxiety Depression Scale), …
- \(c_{ij}=\) Use of resources (drugs, hospital, GP appointments), …
Usually aggregate longitudinal measurements into a cross-sectional summary and for each individual consider the pair \({(e_i,c_i)}\). HTA preferably based on utility-based measures of effectiveness
Quality Adjusted Life Years (QALYs) are a measure of disease burden combining
- Quantity of life (the amount of time spent in a given health state)
- Quality of life (the utility attached to that state)
(“Standard”) cost-effectiveness modelling
- Compute individual QALYs and total costs as
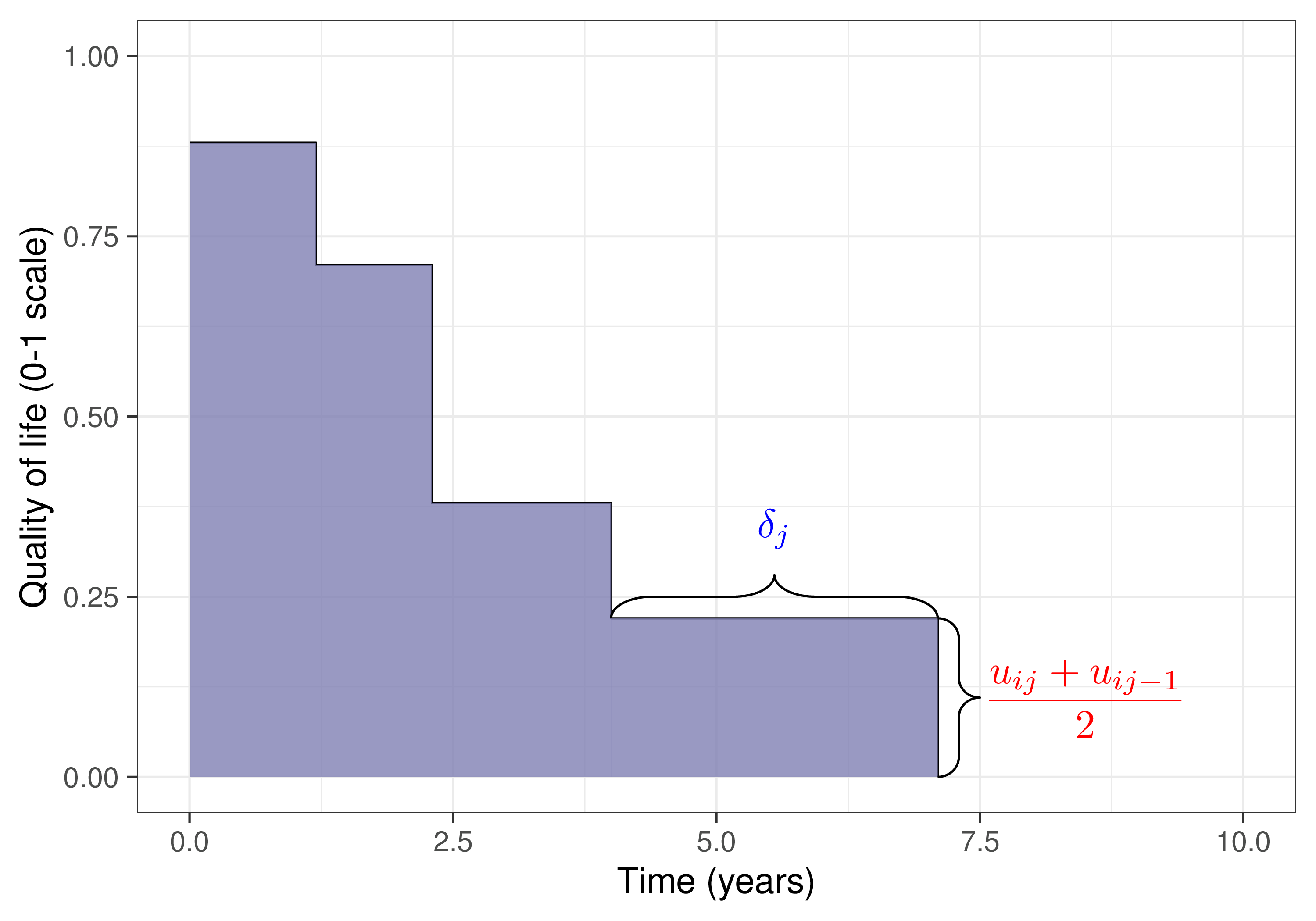
\[\class{myblue}{e_i = \displaystyle\sum_{j=1}^{J} \left(u_{ij}+u_{i\hspace{.5pt}j-1}\right) \frac{\delta_{j}}{2}} \qquad \txt{and} \class{myblue}{\qquad c_i = \sum_{j=0}^J c_{ij}} \qquad \left[\txt{with } \class{myblue}{\delta_j = \frac{\text{Time}_j - \text{Time}_{j-1}}{\txt{Unit of time}}}\right]\]
A QALY is a QALY is a QALY(?)…
(“Standard”) Statistical modelling
- Compute individual QALYs and total costs as
\[\class{myblue}{e_i = \displaystyle\sum_{j=1}^{J} \left(u_{ij}+u_{i\hspace{.5pt}j-1}\right) \frac{\delta_{j}}{2}} \qquad \txt{and} \class{myblue}{\qquad c_i = \sum_{j=0}^J c_{ij}} \qquad \left[\txt{with } \class{myblue}{\delta_j = \frac{\text{Time}_j - \text{Time}_{j-1}}{\txt{Unit of time}}}\right]\]
- (Often implicitly) assume normality and linearity and model independently individual QALYs and total costs by controlling for (centered) baseline values, eg \({u^∗_i = (u_i − \bar{u} )}\) and \({c^∗_i = (c_i − \bar{c} )}\)
\[\begin{align} e_i & = \alpha_{e0} + \alpha_{e1} u^*_{0i} + \alpha_{e2} \text{Trt}_i + \varepsilon_{ei}\, [+ \ldots], \qquad \varepsilon_{ei} \sim \dnorm(0,\sigma_e) \\ c_i & = \alpha_{c0} + \alpha_{c1} c^*_{0i} + \alpha_{c2} \text{Trt}_i + \varepsilon_{ci}\, [+ \ldots], \qquad\hspace{2pt} \varepsilon_{ci} \sim \dnorm(0,\sigma_c) \end{align}\]
- Estimate population average cost and effectiveness differentials
- Under this model specification, these are \(\class{myblue}{\Delta_e=\alpha_{e2}}\) and \(\class{myblue}{\Delta_c=\alpha_{c2}}\)
- Quantify impact of uncertainty in model parameters on the decision making process
- In a fully frequentist analysis, this is done using resampling methods (eg bootstrap)
Example — 10 Top Tips trial
| ID | Trt | Sex | Age | BMI | GP | \(u_0\) | \(u_3\) | \(u_6\) | \(u_{12}\) | \(u_{18}\) | \(u_{24}\) | \(c\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | F | 66 | 1 | 21 | 0.088 | 0.848 | 0.689 | 0.088 | 0.691 | 0.587 | 4230.04 |
| 3 | 1 | M | 57 | 1 | 5 | 0.796 | 0.796 | 0.796 | 0.620 | 0.796 | 1.000 | 1584.88 |
| 4 | 1 | M | 49 | 2 | 5 | 0.725 | 0.727 | 0.796 | 0.848 | 0.796 | 0.291 | 331.27 |
| 12 | 1 | M | 64 | 2 | 14 | 0.850 | 0.850 | 1.000 | 1.000 | 0.848 | 0.725 | 1034.42 |
| 13 | 1 | M | 66 | 1 | 9 | 0.848 | 0.848 | 0.848 | 1.000 | 0.848 | 0.725 | 1321.30 |
| 21 | 1 | M | 64 | 1 | 3 | 0.848 | 1.000 | 1.000 | 1.000 | 0.850 | 1.000 | 520.98 |
- Demographics:
- BMI = Categorised body mas index
- GP = Number of GP visits
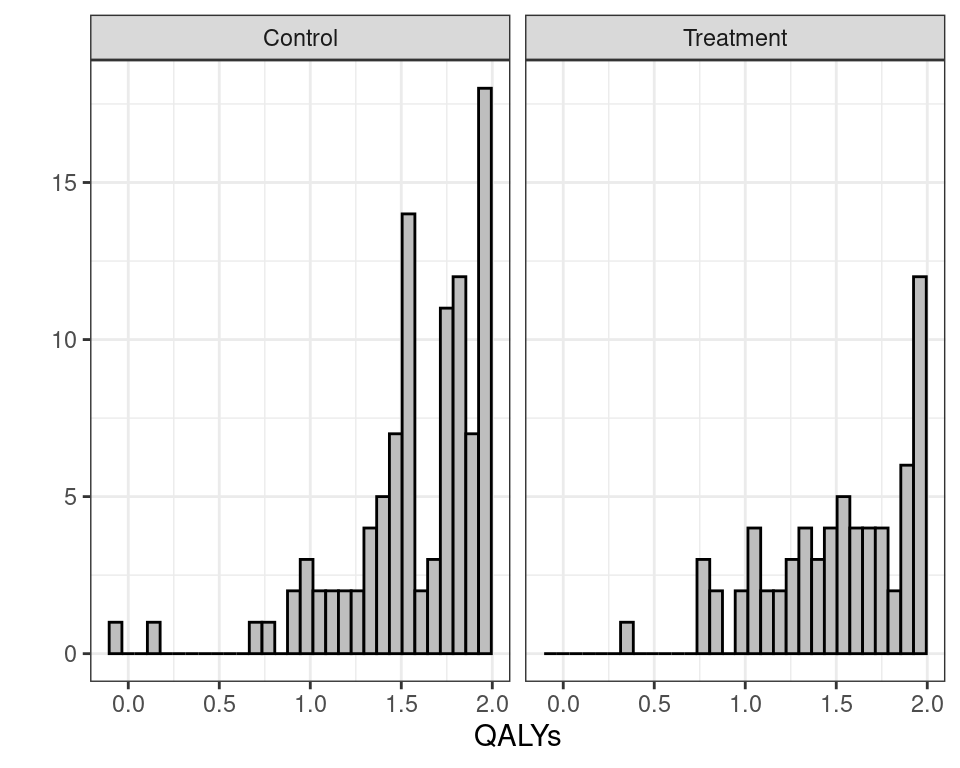
- HRQL data
- QoL measurements at baseline, 3, 6, 12, 18 and 24 months
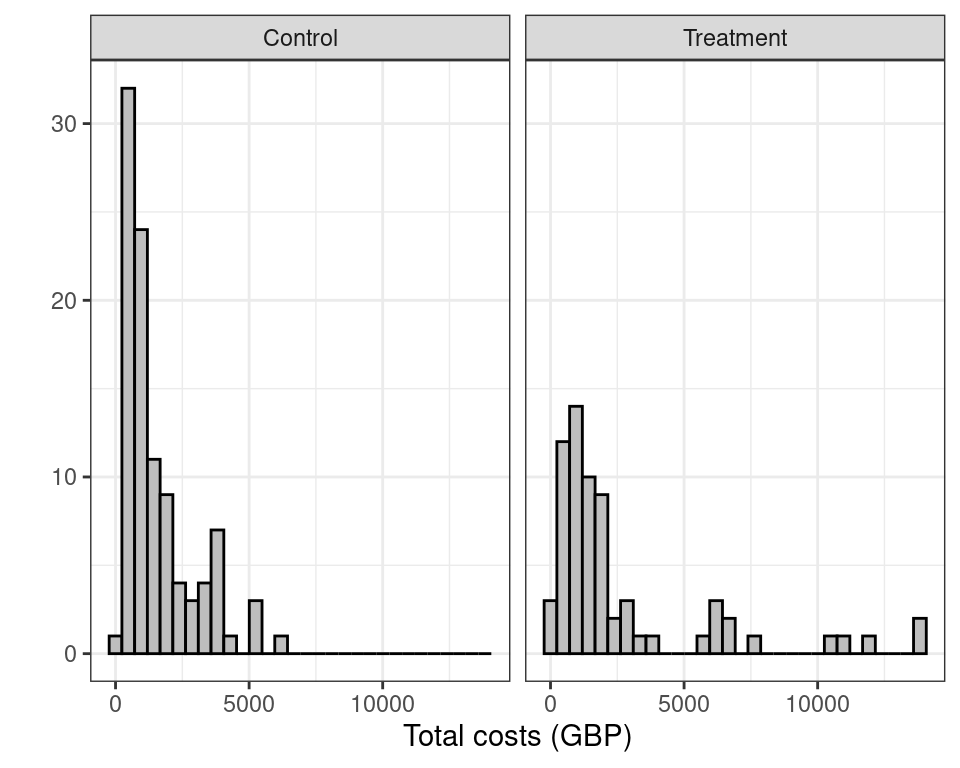
- Costs
- Total costs over the course of the study
Computing the QALYs
# Defines a simple function to do the discounting
disc=function(x, year, disc_rate = 0.035) {
x / ((1 + disc_rate)^(year - 1))
}
# Temporary computation of QoL + QALY with discounting by using long format
df_qol=ttt |>
## select columns of interest
select(id, arm, contains("qol")) |>
## convert dataframe from wide to long format
pivot_longer(
contains("qol"), names_to = "month", names_prefix = "qol_",
names_transform = list(month = as.integer), values_to = "qol"
) |>
# convert month to follow-up year; set baseline to be in year 1
mutate(year = pmax(1, ceiling(month/12))) |>
## apply discounting
mutate(qol_disc = disc(qol, year)) |>
# group by individual
group_by(id) |> mutate(
# time duration between measurements
delta=month-dplyr::lag(month,default = 0),
# sum of utilities between two consecutive time points
du=qol_disc+dplyr::lag(qol_disc,default = 0),
# area under the curve (AUC)
auc=du*delta/2
) |>
# compute the QALYs (in years so divide by 12!), as sum of the AUC
# for all time points
summarise(qaly=sum(auc)/12) |> ungroup()
# Merges the overall QALYs to the main dataset
ttt=ttt |> left_join(df_qol,by=c("id"="id")) |>
mutate(
Trt=arm+1,arm=factor(arm),
arm=case_when(arm=="0"~"Control",TRUE~"Treatment")
)
ttt # A tibble: 167 × 17
id arm sex age bmicat qol_0 qol_3 qol_6 qol_12 qol_18 qol_24 gpvis
<int> <chr> <int> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
1 2 Contr… 1 66 1 0.0880 0.848 0.689 0.0880 0.691 0.587 21
2 3 Contr… 2 57 1 0.796 0.796 0.796 0.62 0.796 1 5
3 4 Contr… 2 49 2 0.725 0.727 0.796 0.848 0.796 0.291 5
4 12 Contr… 2 64 2 0.850 0.850 1 1 0.848 0.725 14
5 13 Contr… 2 66 1 0.848 0.848 0.848 1 0.848 0.725 9
6 21 Contr… 2 64 1 0.848 1 1 1 0.850 1 3
7 23 Contr… 2 57 1 0.62 0.796 0.727 0.691 0.796 1 2
8 24 Contr… 1 37 1 1 1 1 1 1 1 7
9 28 Contr… 2 65 1 1 1 1 1 0.760 1 6
10 35 Contr… 1 33 1 1 1 1 1 1 1 5
# ℹ 157 more rows
# ℹ 5 more variables: costint <dbl>, costoth <dbl>, totalcost <dbl>,
# qaly <dbl>, Trt <dbl>Modelling ILD in HTA
Normal/Normal independent model — model setup
The “standard” modelling is equivalent to
\[\begin{eqnarray*} e_i & \sim & \dnorm(\phi_{ei},\sigma_{et}) \\ \phi_{ei} & = & \alpha_0 + \alpha_1 (\text{Trt}_i - 1) + \alpha_2 (u_{0i}-\bar{u}_{0}) \end{eqnarray*}\] and \[\begin{eqnarray*} c_i & \sim & \dnorm(\phi_{ci},\sigma_{ct}) \\ \phi_{ci} & = & \beta_0 + \beta_2(\text{Trt}_i - 1) \end{eqnarray*}\] where
- \(\text{Trt}_i,t=1,2\) are the two intervention arm (\(t=1\) indicates the standard of care, while \(t=2\) is the active intervention)
- \(u^*_{0i}=(u_{0i}-\bar{u}_{0})\) is the centred baseline QoL
- Consequently
- \(\mu_{et}=\alpha_0 + \alpha_1 (t-1)\) is the population average benefits
- \(\mu_{ct}=\beta_0 + \beta_2(t-1)\) is the population average costs
Modelling ILD in HTA
Normal/Normal independent model — prior distributions
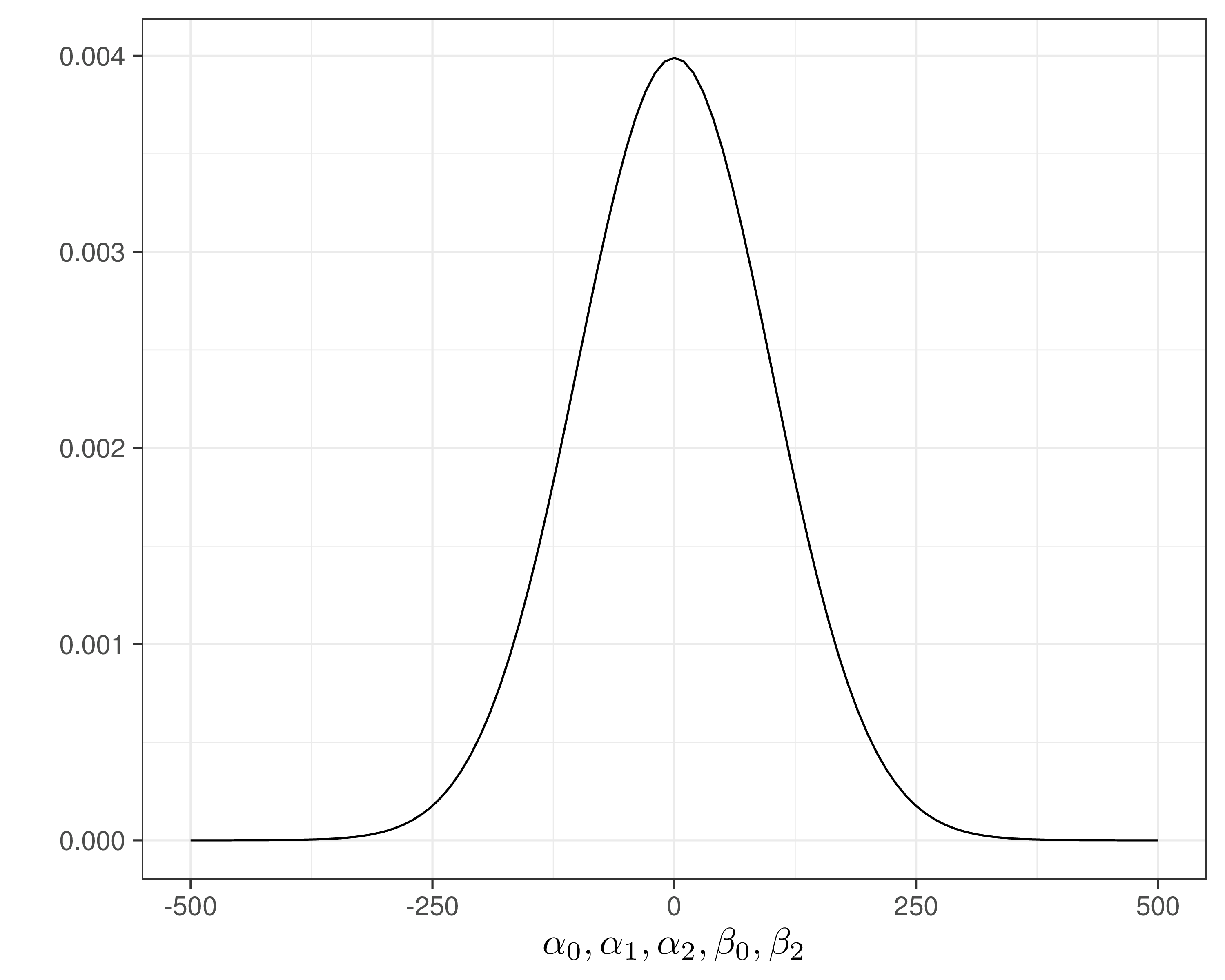
- \(\alpha_0,\alpha_1,\alpha_2,\beta_0,\beta_2 \stackrel{iid}{\sim}\dnorm(\text{mean}=0,\text{sd}=100)\)
- We could probably do much better than this…
- Given the scale of the observed data, unlikely that \(\alpha_0\) and \(\alpha_1\) have such a large range, but given reasonably large sample size, probably won’t matter…
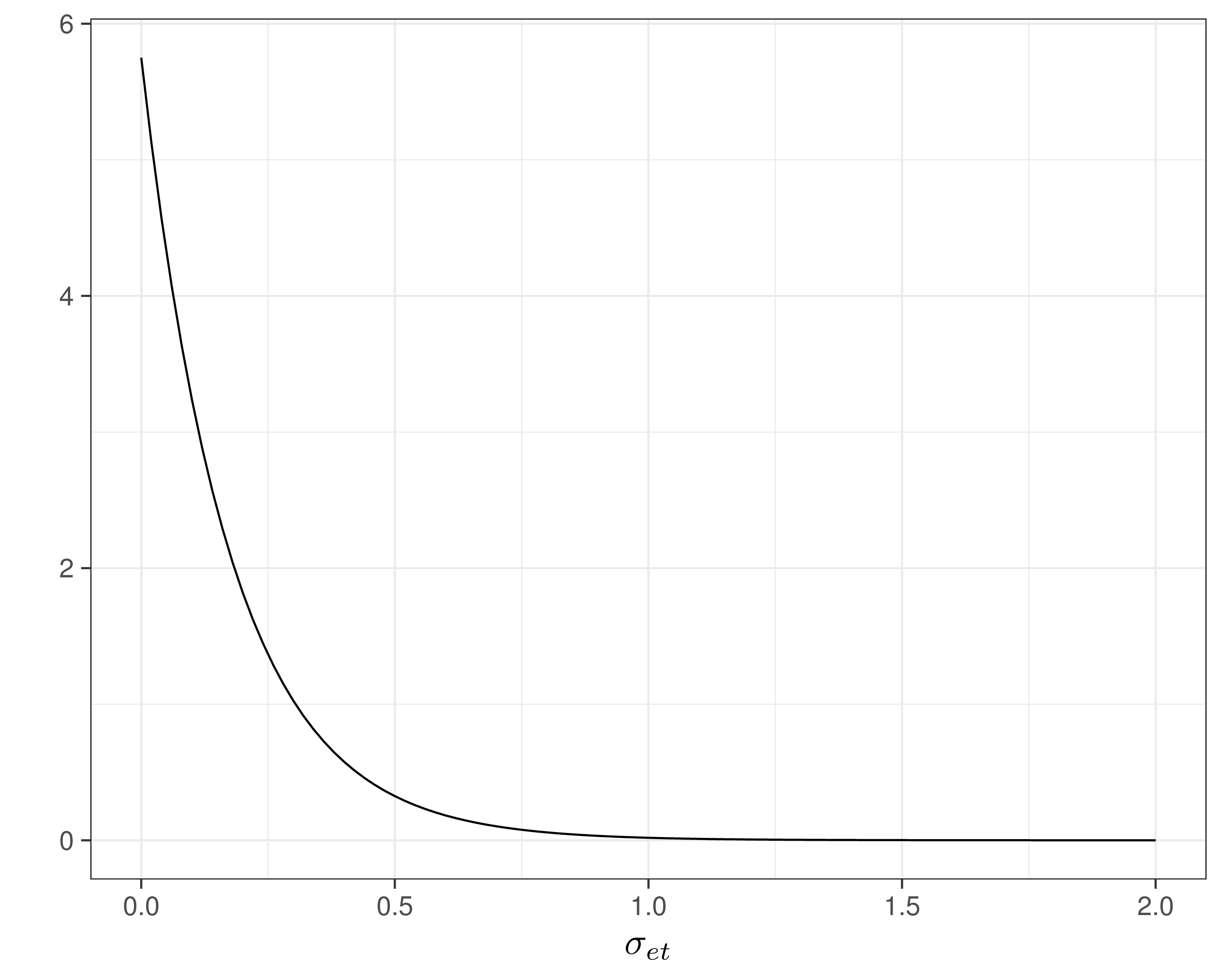
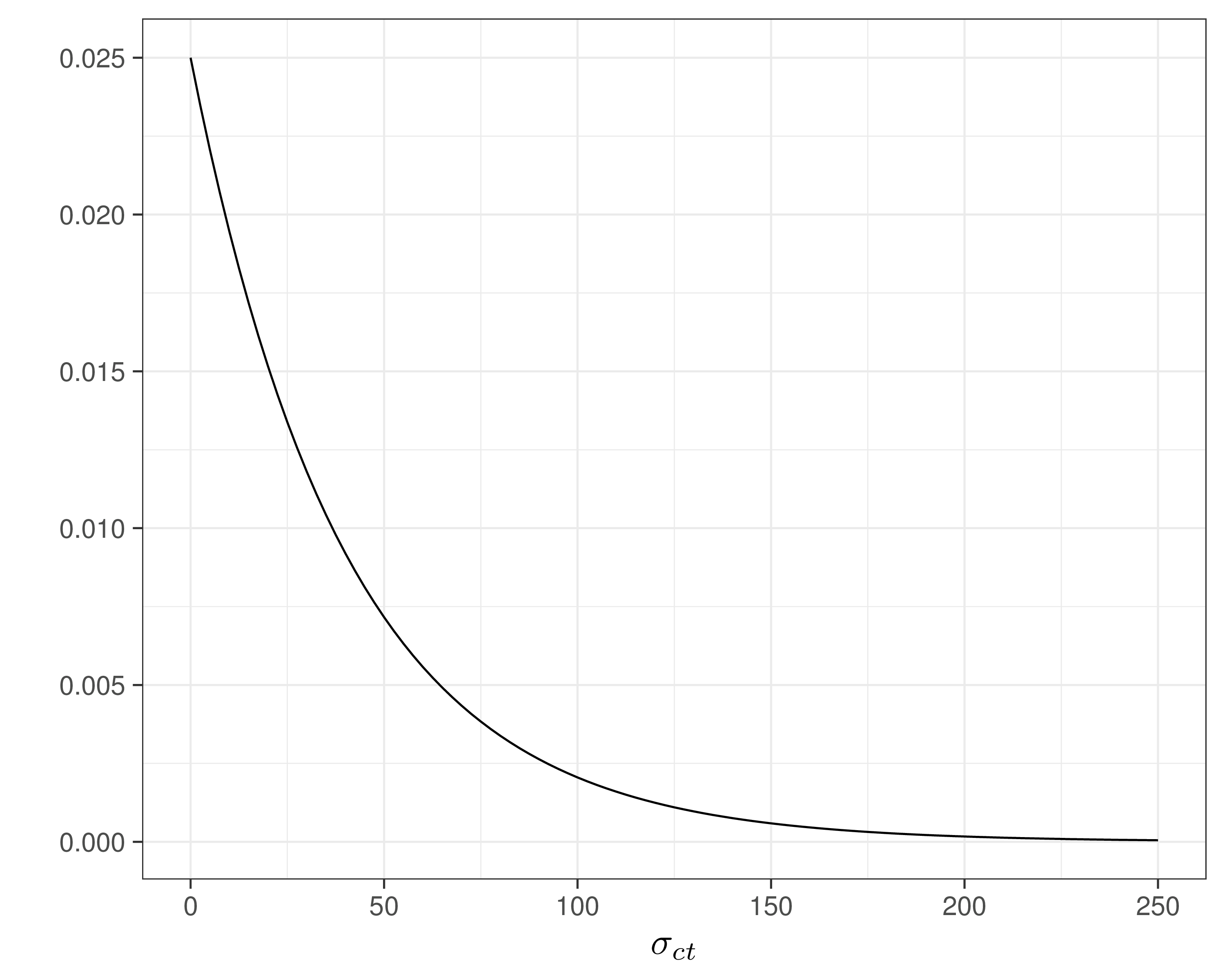
- Assume \(\Pr(\sigma_{et}>0.8)\approx 0.01\) and \(=\Pr(\sigma_{ct}>100)\approx 0.1\) — reasonably vague and minimal assumptions
- Can use a “Penalty Complexity (PC) prior” to encode these into suitable Exponential distributions with rates \(-\frac{\log(0.01)}{0.8}\approx 5.75\) and \(-\frac{\log(0.1)}{100}\approx 0.025\)
Modelling ILD in HTA
Normal/Normal independent model — model code
# Normal/Normal independent model - JAGS code
nn_indep=function(){
for (i in 1:N) {
# Model for the effects
e[i] ~ dnorm(phi.e[i], tau.e[Trt[i]])
phi.e[i] <- alpha0 + alpha1*(Trt[i]-1) + alpha2*u0star[i]
# Model for the costs
c[i] ~ dnorm(phi.c[i], tau.c[Trt[i]])
phi.c[i] <- beta0 + beta2*(Trt[i]-1)
}
# Rescales the main economic parameters
for (t in 1:2) {
mu.e[t] <- alpha0 + alpha1*(t-1)
mu.c[t] <- beta0 + beta2*(t-1)
}
# Minimally informative priors on the regression coefficients
alpha0 ~ dnorm(0,0.0001)
alpha1 ~ dnorm(0,0.0001)
alpha2 ~ dnorm(0,0.0001)
beta0 ~ dnorm(0,0.0001)
beta2 ~ dnorm(0,0.0001)
for (t in 1:2) {
# PC-prior on the sd with Pr(sigma_e>0.8) \approx 0.01
sigma.e[t] ~ dexp(5.75)
tau.e[t] <- pow(sigma.e[t],-2)
# PC-prior on the sd with Pr(sigma_c>100) \approx 0.1
sigma.c[t] ~ dexp(0.025)
tau.c[t] <- pow(sigma.c[t],-2)
}
}- NB:
JAGS(andBUGS…) index the Normal distribution with mean and precision = \(1/\sigma^2\)!
Modelling ILD in HTA
Normal/Normal independent model — running JAGS
# Defines the data list
data=list(e=e,c=c,Trt=Trt,u0star=u0star,N=N)
# Initialises the object 'model' as a list to store all the results
model=list()
# Runs JAGS in the background
library(R2jags)
# Stores the BUGS output as an element named 'nn_indep' in the object 'model'
model$nn_indep=jags(
data=data,
parameters.to.save=c(
"mu.e","mu.c","alpha0","alpha1","alpha2","beta0","beta2","sigma.e","sigma.c"
),
inits=NULL,n.chains=2,n.iter=5000,n.burnin=3000,n.thin=1,DIC=TRUE,
# This specifies the model code as the function 'nn_indep'
model.file=nn_indep
)
# Shows the summary statistics from the posterior distributions.
print(model$nn_indep,digits=3,interval=c(0.025,0.5,0.975))Inference for Bugs model at "/tmp/RtmpMZhrVk/model302f36a5c55d4.txt",
2 chains, each with 5000 iterations (first 3000 discarded)
n.sims = 4000 iterations saved. Running time = 1.296 secs
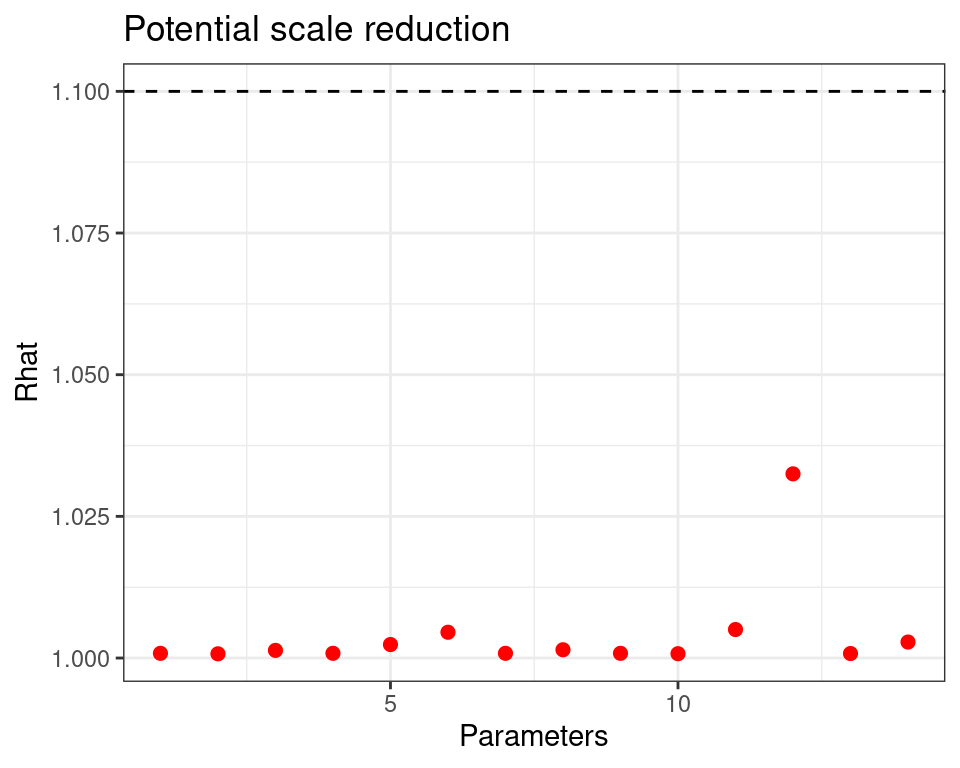
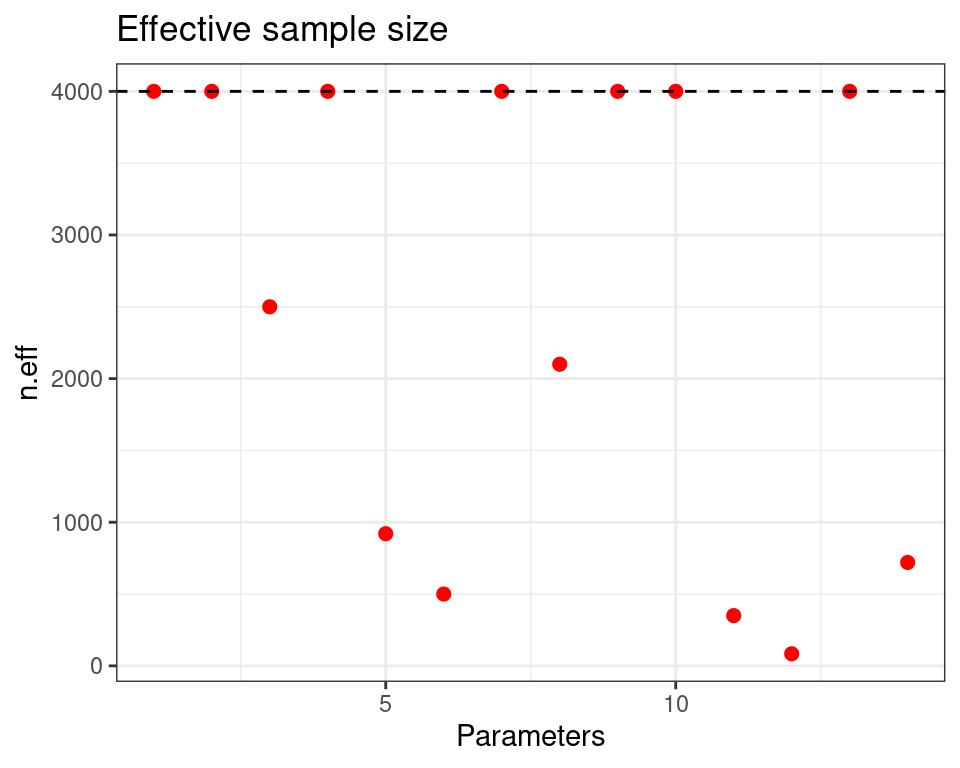
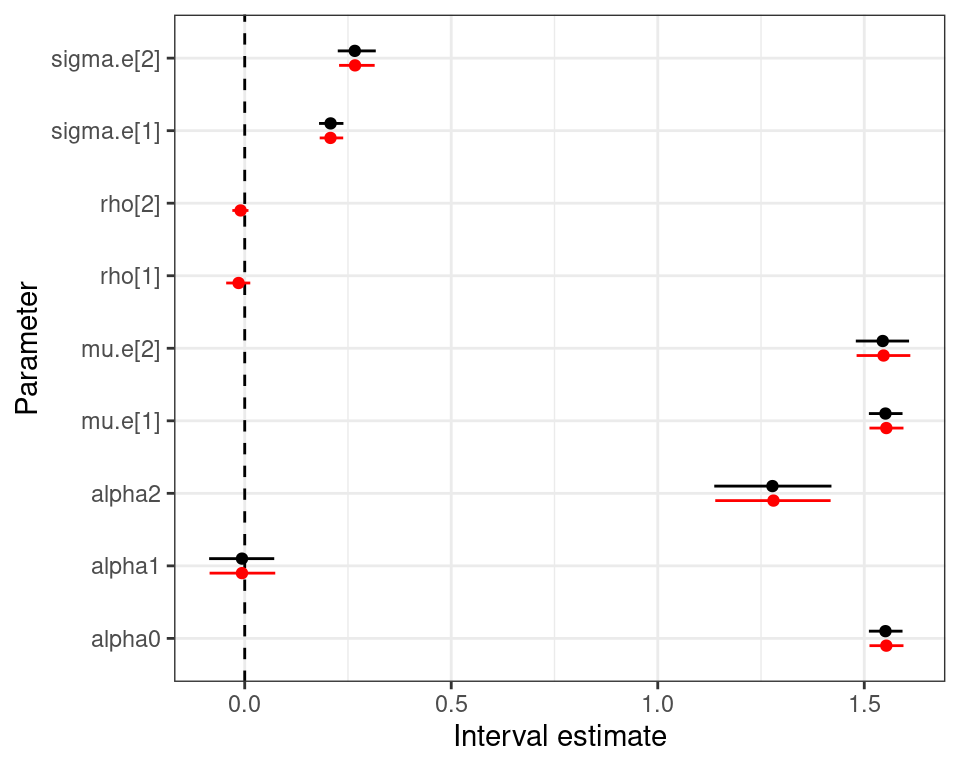
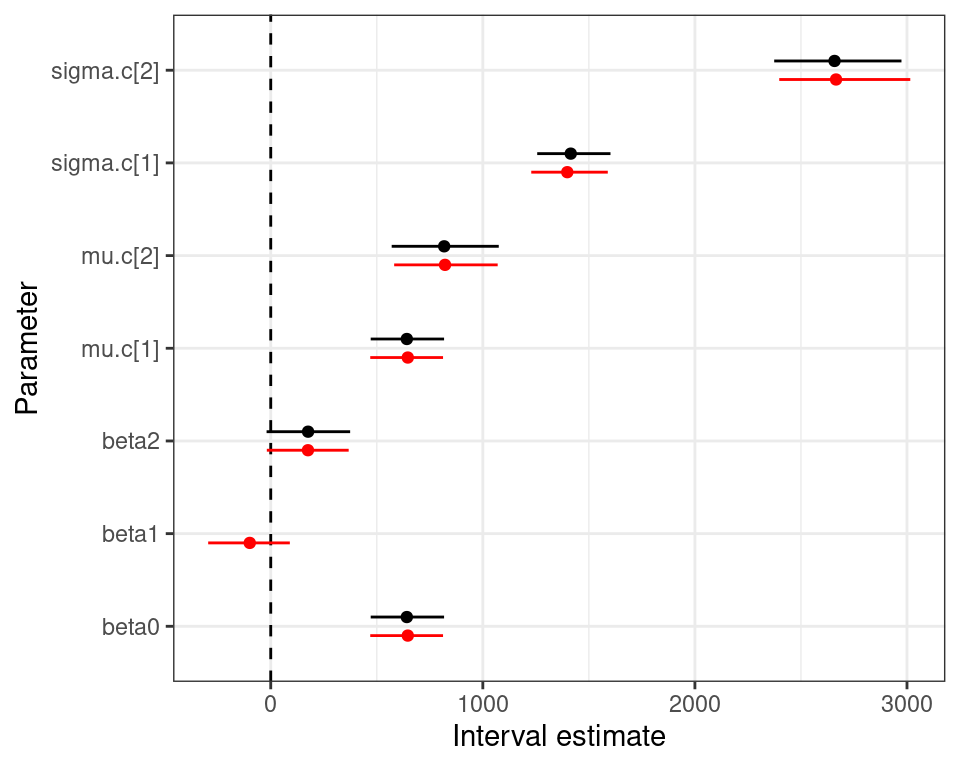
mu.vect sd.vect 2.5% 50% 97.5% Rhat n.eff
alpha0 1.551 0.021 1.511 1.551 1.593 1.001 4000
alpha1 -0.007 0.039 -0.086 -0.007 0.071 1.001 4000
alpha2 1.278 0.072 1.137 1.278 1.421 1.001 2500
beta0 641.695 87.515 471.352 642.276 817.309 1.001 4000
beta2 176.070 99.501 -19.609 175.316 374.427 1.002 920
mu.c[1] 641.695 87.515 471.352 642.276 817.309 1.001 4000
mu.c[2] 817.764 128.646 570.271 818.755 1075.193 1.001 2100
mu.e[1] 1.551 0.021 1.511 1.551 1.593 1.001 4000
mu.e[2] 1.545 0.033 1.480 1.545 1.608 1.001 4000
sigma.c[1] 1414.597 89.208 1256.438 1411.066 1601.913 1.005 350
sigma.c[2] 2658.376 154.480 2373.838 2653.705 2973.944 1.033 84
sigma.e[1] 0.208 0.015 0.180 0.207 0.239 1.001 4000
sigma.e[2] 0.267 0.024 0.225 0.265 0.317 1.003 720
deviance 3063.112 12.397 3039.937 3062.619 3088.360 1.005 500
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule: pV = var(deviance)/2)
pV = 76.7 and DIC = 3139.8
DIC is an estimate of expected predictive error (lower deviance is better).Modelling ILD in HTA
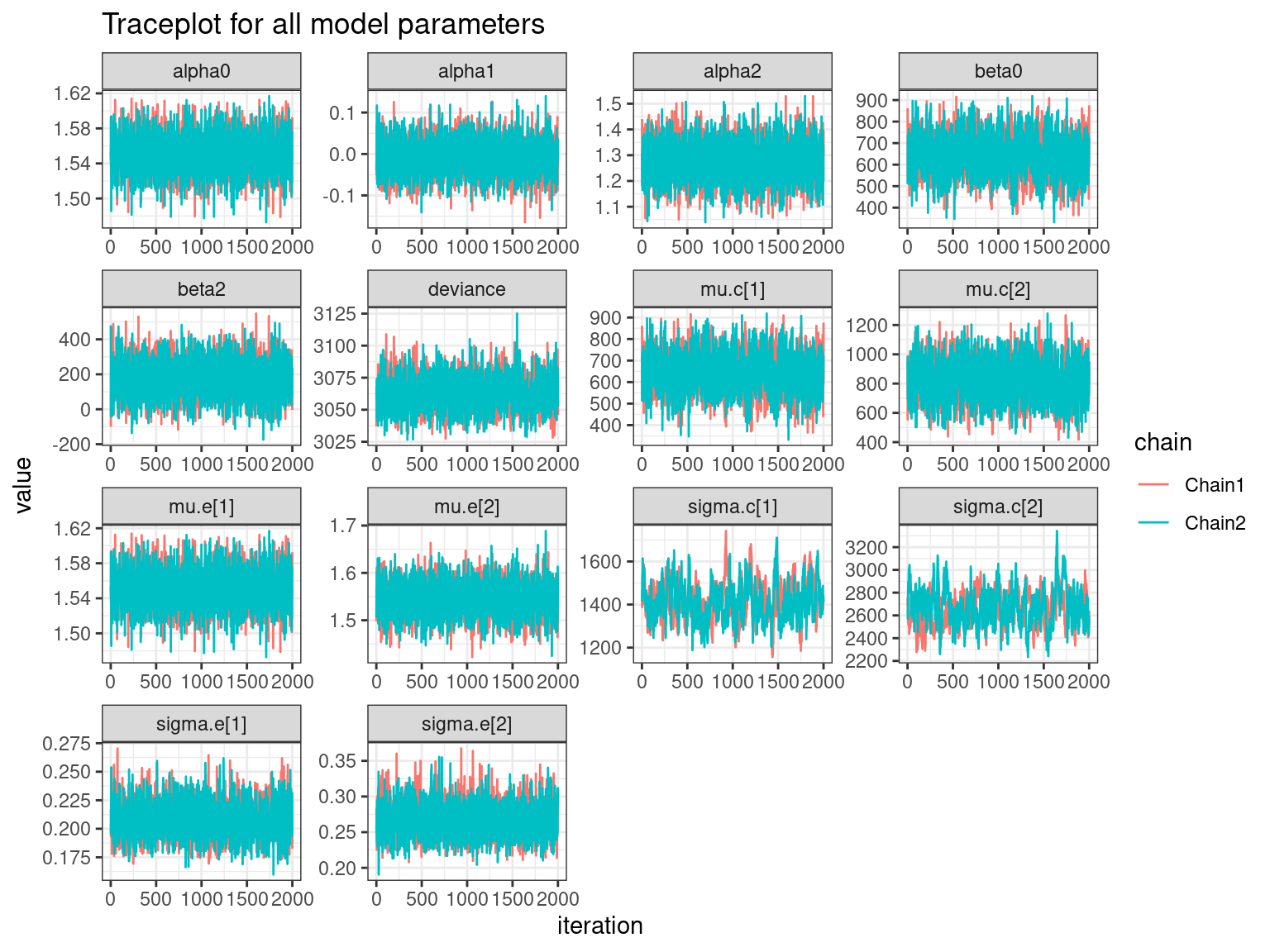
Normal/Normal independent model — diagnostics
Modelling ILD in HTA
Normal/Normal independent model — diagnostics
Modelling ILD in HTA
Normal/Normal independent model — diagnostics
What’s wrong with this?…
- Potential correlation between costs & clinical benefits (Individual level + Aggregated level Data)
- Strong positive correlation – effective treatments are innovative and result from intensive and lengthy research \(\Rightarrow\) are associated with higher unit costs
- Negative correlation - more effective treatments may reduce total care pathway costs e.g. by reducing hospitalisations, side effects, etc.
- Because of the way in which standard models are set up, bootstrapping generally only approximates the underlying level of correlation – (MCMC does a better job!)
- Joint/marginal normality not realistic (Mainly ILD)
- Costs usually skewed and benefits may be bounded in \([0; 1]\)
- Can use transformation (e.g. logs) – but care is needed when back transforming to the natural scale
- Should use more suitable models (e.g. Beta, Gamma or log-Normal) – (generally easier under a Bayesian framework)
- Particularly relevant in presence of partially observed data – more on this later!
- Particularly as the focus is on decision-making (rather than just inference), we need to use all available evidence to fully characterise current uncertainty on the model parameters and outcomes (Mainly ALD)
- A Bayesian approach is helpful in combining different sources of information
- (Propagating uncertainty is a fundamentally Bayesian operation!)
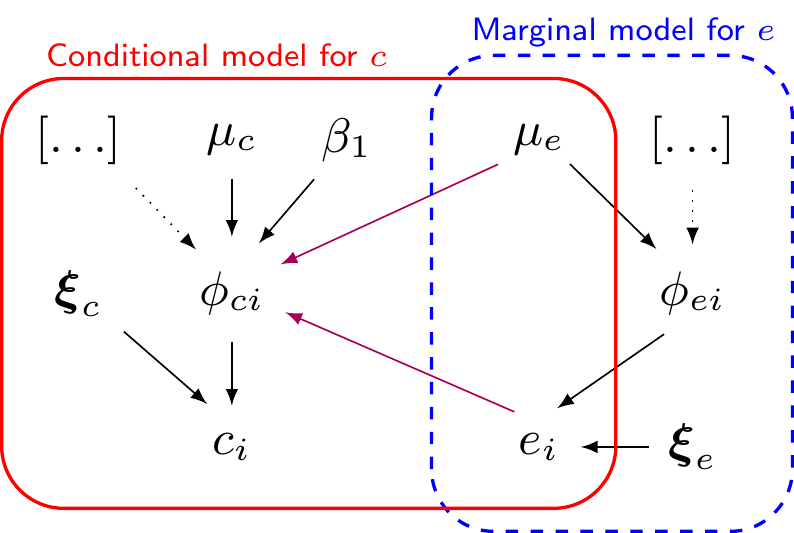
Marginal/conditional factorisation model
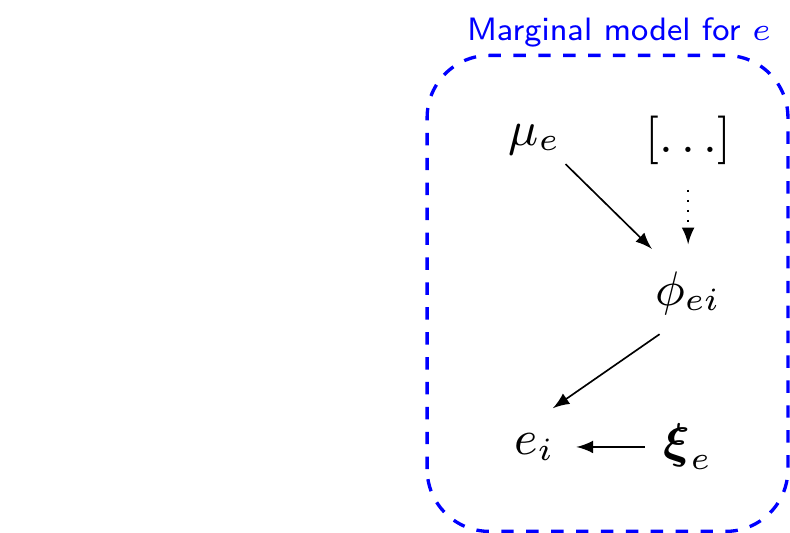
- In general, can represent the joint distribution as \(\class{myblue}{p(e,c) = p(e)p(c\mid e) = p(c)p(e\mid c)}\)
Marginal/conditional factorisation model
- In general, can represent the joint distribution as \(\class{myblue}{p(e,c) = }\class{blue}{p(e)}\class{myblue}{p(c\mid e) = p(c)p(e\mid c)}\)
\[\begin{eqnarray*} e_i & \sim & p(e \mid \phi_{ei},\bm\xi_e) \\ g_e(\phi_{ei}) & = & \alpha_0 \, [+\ldots] \\ \mu_e & = & g_e^{-1}(\alpha_0) \\ && \\ \phi_{ei} & = & \style{font-family:inherit;}{\text{location}} \\ \bm\xi_e & = & \style{font-family:inherit;}{\text{ancillary}} \end{eqnarray*}\]
Marginal/conditional factorisation model
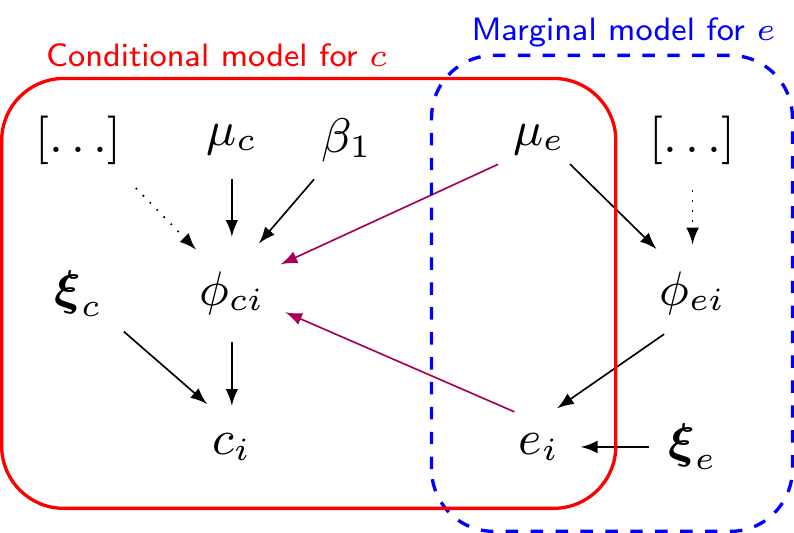
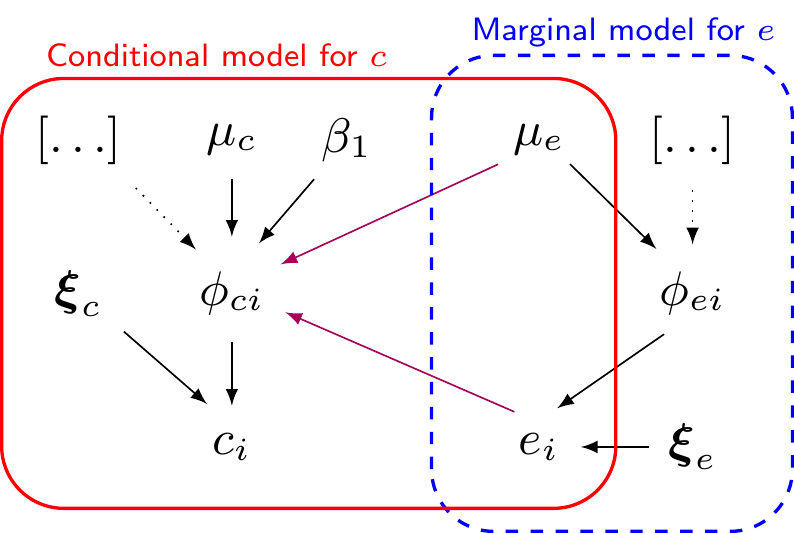
- In general, can represent the joint distribution as \(\class{myblue}{p(e,c) = }\class{blue}{p(e)}\class{red}{p(c\mid e)}\class{myblue}{ = p(c)p(e\mid c)}\)
\[\begin{eqnarray*} e_i & \sim & p(e \mid \phi_{ei},\bm\xi_e) \\ g_e(\phi_{ei}) & = & \alpha_0 \, [+\ldots] \\ \mu_e & = & g_e^{-1}(\alpha_0) \\ && \\ \phi_{ei} & = & \style{font-family:inherit;}{\text{location}} \\ \bm\xi_e & = & \style{font-family:inherit;}{\text{ancillary}} \end{eqnarray*}\]
\[\begin{eqnarray*} c_i & \sim & p(c \mid e_i, \phi_{ci},\bm\xi_c) \\ g_c(\phi_{ci}) & = & \beta_0 +\beta_1(e_i - \mu_e) \, [+\ldots] \\ \mu_c & = & g_c^{-1}(\beta_0) \\ && \\ \phi_{ci} & = & \style{font-family:inherit;}{\text{location}} \\ \bm\xi_c & = & \style{font-family:inherit;}{\text{ancillary}} \end{eqnarray*}\]
Marginal/conditional factorisation model
- In general, can represent the joint distribution as \(\class{myblue}{p(e,c) = p(e)p(c\mid e) = p(c)p(e\mid c)}\)
\[\begin{eqnarray*} e_i & \sim & \dnorm(\phi_{ei},\xi_e) \\ \phi_{ei} & = & \alpha_0 \, [+\ldots] \\ \mu_e & = & \alpha_0 \\ && \\ \phi_{ei} & = & \style{font-family:inherit;}{\text{marginal mean}} \\ \xi_e & = & \style{font-family:inherit;}{\text{marginal sd}} \\ g_e(\cdot) & = & \style{font-family:inherit;}{\text{identity}} \end{eqnarray*}\]
\[\begin{eqnarray*} c_i & \sim & \dnorm(\phi_{ci},\xi_c) \\ \phi_{ci} & = & \beta_0 +\beta_1(e_i - \mu_e) \, [+\ldots] \\ \mu_c & = & \beta_0 \\ && \\ \phi_{ci} & = & \style{font-family:inherit;}{\text{conditional mean}} \\ \xi_c & = & \style{font-family:inherit;}{\text{conditional sd}} \\ g_c(\cdot) & = & \style{font-family:inherit;}{\text{identity}} \end{eqnarray*}\]
- Normal/Normal MCF — equivalent to
\[\left( \begin{array}{c} \varepsilon_{ei} \\ \varepsilon_{ci}\end{array} \right) \sim \dnorm\left( \left(\begin{array}{c} 0 \\ 0\end{array}\right), \left(\begin{array}{cc} \sigma^2_e & \rho\sigma_e\sigma_c \\ & \sigma^2_c \end{array}\right) \right)\]
- Can also write down analytically the marginal mean and sd for the costs (but that’s not so relevant…)
Marginal/conditional factorisation model
- In general, can represent the joint distribution as \(\class{myblue}{p(e,c) = p(e)p(c\mid e) = p(c)p(e\mid c)}\)
\[\begin{eqnarray*} e_i & \sim & \dbeta(\phi_{ei}\xi_e,(1-\phi_{ei})\xi_e) \\ \logit(\phi_{ei}) & = & \alpha_0 \, [+\ldots] \\ \mu_e & = & \frac{\exp(\alpha_0)}{1+\exp(\alpha_0)} \\ && \\ \phi_{ei} & = & \style{font-family:inherit;}{\text{marginal mean}} \\ \xi_e & = & \style{font-family:inherit;}{\text{marginal scale}} \\ g_e(\cdot) & = & \style{font-family:inherit;}{\text{logit}} \end{eqnarray*}\]
\[\begin{eqnarray*} c_i & \sim & \dgamma(\xi_c,\xi_c/\phi_{ci}) \\ \log(\phi_{ci}) & = & \beta_0 +\beta_1(e_i - \mu_e) \, [+\ldots] \\ \mu_c & = & \exp(\beta_0) \\ && \\ \phi_{ci} & = & \style{font-family:inherit;}{\text{conditional mean}} \\ \xi_c & = & \style{font-family:inherit;}{\text{shape}} \\ \xi_c/\phi_{ci} & = & \style{font-family:inherit;}{\text{rate}} \\ g_c(\cdot) & = & \style{font-family:inherit;}{\text{log}} \end{eqnarray*}\]
- Beta/Gamma MCF
- Effects may be bounded in \([0;1]\) (e.g. QALYs on a one-year horizon)
- Costs are positive and skewed
- …
Marginal/conditional factorisation model
- In general, can represent the joint distribution as \(\class{myblue}{p(e,c) = p(e)p(c\mid e) = p(c)p(e\mid c)}\)
\[\begin{eqnarray*} e_i & \sim & p(e \mid \phi_{ei},\bm\xi_e) \\ g_e(\phi_{ei}) & = & \alpha_0 \, [+\ldots] \\ \mu_e & = & g_e^{-1}(\alpha_0) \\ && \\ \phi_{ei} & = & \style{font-family:inherit;}{\text{location}} \\ \bm\xi_e & = & \style{font-family:inherit;}{\text{ancillary}} \end{eqnarray*}\]
\[\begin{eqnarray*} c_i & \sim & p(c \mid e_i, \phi_{ci},\bm\xi_c) \\ g_c(\phi_{ci}) & = & \beta_0 +\beta_1(e_i - \mu_e) \, [+\ldots] \\ \mu_c & = & g_c^{-1}(\beta_0) \\ && \\ \phi_{ci} & = & \style{font-family:inherit;}{\text{location}} \\ \bm\xi_c & = & \style{font-family:inherit;}{\text{ancillary}} \end{eqnarray*}\]
Combining “modules” and fully characterising uncertainty about deterministic functions of random quantities is relatively straightforward using MCMC
Prior information can help stabilise inference (especially with sparse data!), eg
- Cancer patients are unlikely to survive as long as the general population
- ORs are unlikely to be greater than \(\pm \style{font-family:inherit;}{\text{5}}\)
To be or not to be?… (A Bayesian)
In principle, there’s nothing inherently Bayesian about MCF… BUT: there’s lots of advantages in doing it in a Bayesian setup
- As the model becomes more and more realistic and its structure more and more complex, to account for skeweness and correlation, the computational advantages of using maximum likelihood estimations become increasingly smaller
- Writing and optimising the likelihood function becomes more complex analytically and even numerically and might require the use of simulation althorithms
- Bayesian models generally scale up with minimal changes
- Computation may be more expensive, but the marginal computational cost is in fact diminishing
- Realistic models are usually based on highly non-linear transformations
- from a Bayesian perspective, this does not pose a substantial problem, because once we obtain simulations from the posterior distribution for \(\alpha_0\) and \(\beta_0\), it is possible to simply rescale them to obtain samples from the posterior distribution of \(\mu_e\) and \(\mu_c\)
- This allows us to fully characterise and propagate the uncertainty in the fundamental economic parameters to the rest of the decision analysis with essentially no extra computational cost
- Frequentist/ML approach would resort to resampling methods, such as the bootstrap to effectively produce an approximation to the joint posterior distribution for all the model parameters \(\bm\theta\) and any function thereof
- Prior information can help stabilise inference
- Most often, we do have contextual information to mitigate limited evidence from the data and stabilise the evidence
- Using a Bayesian approach allows us to use this contextual information in a principled way.
Normal/Normal MCF — 10TT
\[\begin{align*} e_i \sim \dnorm(\phi_{ei},\tau_{et}) && \phi_{ei} &= \alpha_0 +\alpha_1(\text{Trt}_i - 1) + \alpha_2 u^*_{0i} && \mu_{et} = \alpha_0 + \alpha_1(t-1) \\ c_i\mid e_i \sim \dnorm(\phi_{ci},\tau_{ct}) && \phi_{ci} &= \beta_0 + \beta_1(e_i -\mu_e) + \beta_2(\text{Trt}_i - 1) && \mu_{ct} = \beta_0 + \beta_2(t-1), \end{align*}\]
Normal/Normal MCF — model code
# Normal/Normal MCF - JAGS code
nn_mcf=function(){
for (i in 1:N) {
# Marginal model for the effects
e[i] ~ dnorm(phi.e[i], tau.e[Trt[i]])
phi.e[i] <- alpha0 + alpha1*(Trt[i]-1) + alpha2*u0star[i]
# *Conditional* model for the costs
c[i] ~ dnorm(phi.c[i], tau.c[Trt[i]])
phi.c[i] <- beta0 + beta1*(e[i]-mu.e[Trt[i]]) + beta2*(Trt[i]-1)
}
# Rescales the main economic parameters
for (t in 1:2) {
mu.e[t] <- alpha0 + alpha1*(t-1)
mu.c[t] <- beta0 + beta2*(t-1)
}
# Minimally informative priors on the regression coefficients
alpha0 ~ dnorm(0,0.0001)
alpha1 ~ dnorm(0,0.0001)
alpha2 ~ dnorm(0,0.0001)
beta0 ~ dnorm(0,0.0001)
beta1 ~ dnorm(0,0.0001)
beta2 ~ dnorm(0,0.0001)
for (t in 1:2) {
# PC-prior on the *marginal* sd with Pr(sigma_e>0.8) \approx 0.01
sigma.e[t] ~ dexp(5.75)
tau.e[t] <- pow(sigma.e[t],-2)
# PC-prior on the *conditional* sd with Pr(lambda_c>100) \approx 0.1
lambda.c[t] ~ dexp(0.025)
tau.c[t] <- pow(lambda.c[t],-2)
# Retrieves the correlation coefficients
rho[t] <- beta1*sigma.e[t]/sigma.c[t]
# And the *marginal* standard deviation for the cost
sigma.c[t] <- sqrt(pow(lambda.c[t],2) + pow(sigma.e[t],2)*pow(beta1,2))
}
}Normal/Normal MCF — 10TT
Normal/Normal MCF — running JAGS
# Runs JAGS in the background and stores the output in the element 'nn_mcf'
model$nn_mcf=jags(
data=data,
parameters.to.save=c(
"mu.e","mu.c","alpha0","alpha1","alpha2","beta0","beta1","beta2",
"sigma.e","sigma.c","lambda.c","rho"
),
inits=NULL,n.chains=2,n.iter=5000,n.burnin=3000,n.thin=1,DIC=TRUE,
# This specifies the model code as the function 'nn_mcf'
model.file=nn_mcf
)
# Shows the summary statistics from the posterior distributions.
print(model$nn_mcf,digits=3,interval=c(0.025,0.5,0.975))Inference for Bugs model at "/tmp/RtmpMZhrVk/model302f348dda90f.txt",
2 chains, each with 5000 iterations (first 3000 discarded)
n.sims = 4000 iterations saved. Running time = 1.721 secs
mu.vect sd.vect 2.5% 50% 97.5% Rhat n.eff
alpha0 1.553 0.021 1.513 1.553 1.595 1.001 4000
alpha1 -0.007 0.040 -0.085 -0.007 0.074 1.002 1100
alpha2 1.280 0.072 1.139 1.280 1.419 1.001 3400
beta0 646.215 86.737 469.189 647.240 812.420 1.002 1100
beta1 -98.897 97.265 -294.985 -99.959 90.051 1.001 4000
beta2 175.534 98.729 -18.429 174.422 367.519 1.009 170
lambda.c[1] 1397.942 92.399 1228.269 1391.504 1588.781 1.014 110
lambda.c[2] 2665.250 156.820 2397.608 2655.034 3014.849 1.102 20
mu.c[1] 646.215 86.737 469.189 647.240 812.420 1.002 1100
mu.c[2] 821.749 127.323 581.961 822.601 1070.099 1.003 640
mu.e[1] 1.553 0.021 1.513 1.553 1.595 1.001 4000
mu.e[2] 1.547 0.034 1.481 1.547 1.611 1.002 1400
rho[1] -0.015 0.015 -0.045 -0.015 0.013 1.001 4000
rho[2] -0.010 0.010 -0.030 -0.010 0.009 1.002 1700
sigma.c[1] 1398.244 92.361 1228.365 1391.574 1589.238 1.014 110
sigma.c[2] 2665.512 156.790 2397.632 2655.344 3015.506 1.102 20
sigma.e[1] 0.208 0.015 0.182 0.206 0.238 1.004 4000
sigma.e[2] 0.267 0.022 0.228 0.265 0.315 1.001 4000
deviance 3060.918 12.375 3038.076 3060.516 3087.085 1.024 72
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule: pV = var(deviance)/2)
pV = 75.5 and DIC = 3136.4
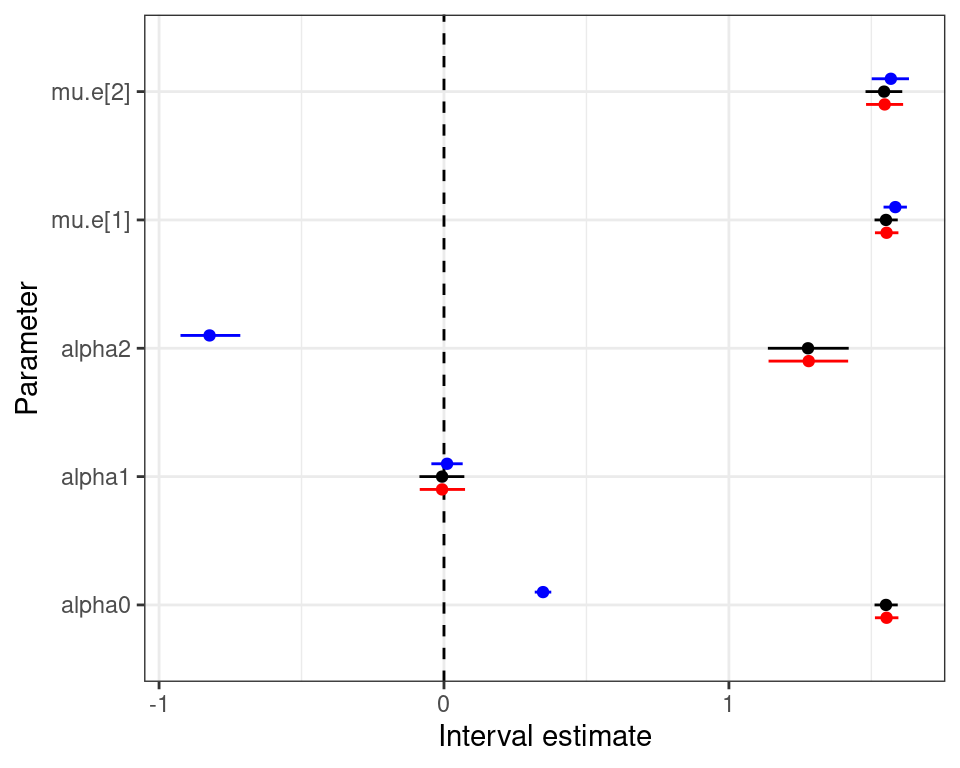
DIC is an estimate of expected predictive error (lower deviance is better).Normal/Normal independent vs Normal/Normal MCF — 10TT
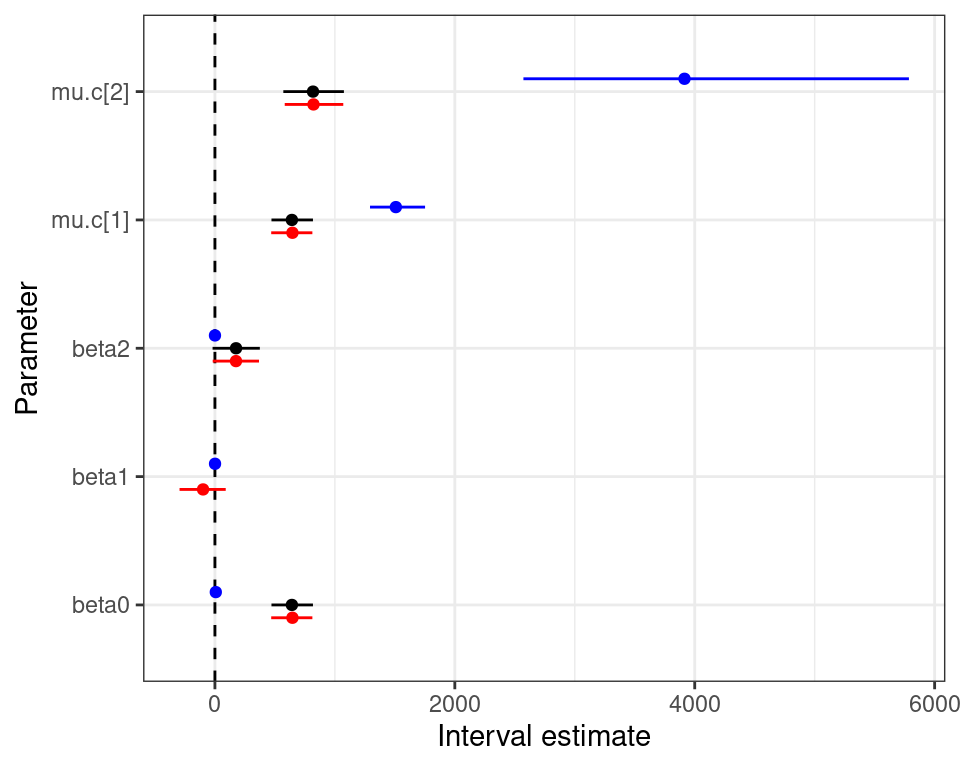
Normal/Normal independent Normal/Normal MCF
Data transformation
- There’s a couple of complications with the effect data
- Exhibit large left skewness
- A small number of individuals are associated with negative QALYs, indicating a very poor health state (“worse than death”)
- Easy solution: rescale and define
\[e^*_i = (3 -e_i)\]
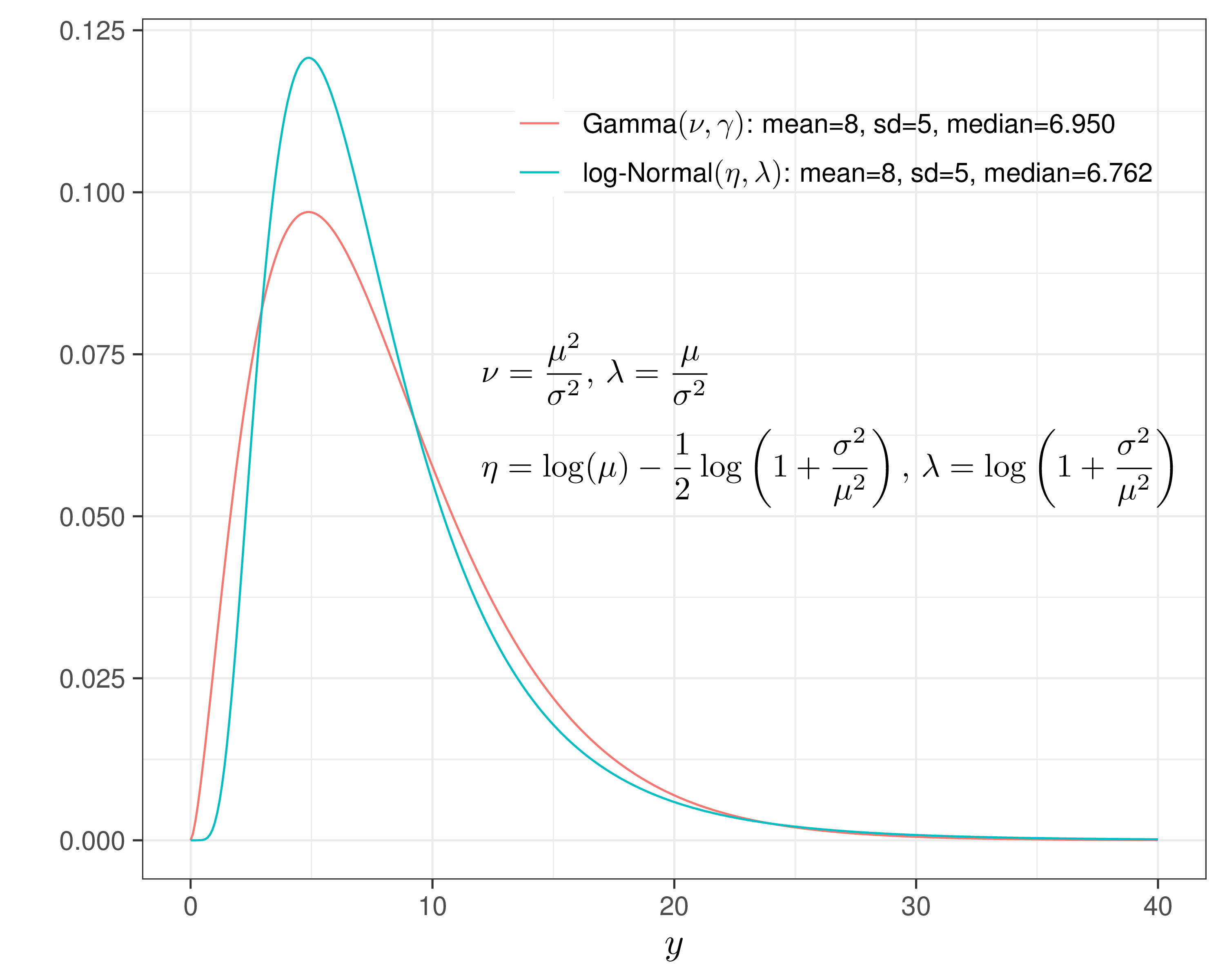
- This rescales the observed QALYs and turns the distribution into a right skewed, which means we can use a Gamma distribution to model the sampling variability
Gamma/Gamma MCF — 10TT
\[\begin{align*} e^*_{i} \sim \dgamma (\nu_e,\gamma_{ei}) && & \log(\phi_{ei}) = \alpha_0 + \alpha_1(\text{Trt}_i - 1) + \alpha_2 u^*_{0i}\\ c_i\mid e^*_i \sim \dgamma(\nu_c,\gamma_{ci}) && & \log(\phi_{ci}) = \beta_0 + \beta_1(e^*_i -\mu^*_e) + \beta_2(\text{Trt}_i - 1), \end{align*}\] where, because of the properties of the Gamma distribution
- \(\phi_{ei}\) indicates the marginal mean for the QALYs,
- \(\nu_e\) is the shape
- \(\gamma_{ei}=\nu_c/\phi_{ei}\) is the rate
Similarly
- \(\nu_c\) is the shape
- \(\gamma_{ci}=\nu_c/\phi_{ci}\) is the rate of the conditional distribution for the costs given the benefits
- \(\phi_{ci}\) is the conditional mean
Gamma/Gamma MCF — 10TT
Prior distributions
- Keep the very vague, minimally informative priors for the regression coefficients
- Again, we could probably do better here, considering that both \(\phi_{ei}\) and \(\phi_{ci}\) are defined on a log scale and thus we are implying a very large range in the priors
- Sensitivity analysis may be very important to this aspect
- As for the shape parameters \(\nu_{et}\) and \(\nu_{ct}\), we specify again a PC prior
- Generally speaking, it is more difficult to encode genuine prior knowledge on this scale
- Thus we start by including a fairly vague specification, where we assume that \(\Pr(\nu_{et}>30)=\Pr(\nu_{ct}>30)\approx 0.01\) — this implies an Exponential with rate \(-\frac{\log(0.01)}{30}\approx 0.15\)
Gamma/Gamma MCF — 10TT
Gamma/Gamma MCF — model code
# Gamma/Gamma MCF - JAGS code
gg_mcf=function(){
for (i in 1:N) {
# Marginal model for the *rescaled* effects
estar[i] ~ dgamma(nu.e[Trt[i]], gamma.e[Trt[i],i])
gamma.e[Trt[i],i] <- nu.e[Trt[i]]/phi.e[i]
log(phi.e[i]) <- alpha0 + alpha1*(Trt[i]-1) + alpha2*u0star[i]
# Conditional model for the costs
c[i] ~ dgamma(nu.c[Trt[i]], gamma.c[Trt[i],i])
gamma.c[Trt[i],i] <- nu.c[Trt[i]]/phi.c[i]
log(phi.c[i]) <- beta0 + beta1*(estar[i]-mustar.e[Trt[i]]) + beta2*(Trt[i]-1)
}
# Rescales the main economic parameters
for (t in 1:2) {
mustar.e[t] <- exp(alpha0 + alpha1*(t-1))
mu.e[t] <- 3 - mustar.e[t]
mu.c[t] <- exp(beta0 + beta1*(t-1))
}
# Minimally informative priors on the regression coefficients
alpha0 ~ dnorm(0,0.0001)
alpha1 ~ dnorm(0,0.0001)
alpha2 ~ dnorm(0,0.0001)
beta0 ~ dnorm(0,0.0001)
beta1 ~ dnorm(0,0.0001)
beta2 ~ dnorm(0,0.0001)
# PC prior on the shape parameters
# assume that Pr(nu.e>30) = Pr(nu.c>30) \approx 0.01
for (t in 1:2) {
nu.e[t] ~ dexp(0.15)
nu.c[t] ~ dexp(0.15)
}
}Gamma/Gamma MCF — 10TT
Gamma/Gamma MCF — running JAGS
# Defines the rescaled QALYs in the data list and remove the old version
data$estar=3-data$e
# Runs JAGS in the background and stores the output in the element 'gg_mcf'
model$gg_mcf=jags(
data=data,
parameters.to.save=c(
"mu.e","mustar.e","mu.c","alpha0","alpha1","alpha2","beta0",
"beta1","beta2","nu.e","nu.c"
),
inits=NULL,n.chains=2,n.iter=5000, n.burnin=3000,n.thin=1,DIC=TRUE,
# This specifies the model code as the function 'model.code'
model.file=gg_mcf
)
# Shows the summary statistics from the posterior distributions.
print(model$gg_mcf,digits=3,interval=c(0.025,0.5,0.975))Inference for Bugs model at "/tmp/RtmpMZhrVk/model302f3627ed054.txt",
2 chains, each with 5000 iterations (first 3000 discarded)
n.sims = 4000 iterations saved. Running time = 21.4 secs
mu.vect sd.vect 2.5% 50% 97.5% Rhat n.eff
alpha0 0.348 0.015 0.319 0.348 0.377 1.002 1900
alpha1 0.011 0.028 -0.044 0.011 0.066 1.001 2200
alpha2 -0.823 0.053 -0.925 -0.823 -0.715 1.001 2300
beta0 7.316 0.077 7.165 7.313 7.468 1.003 550
beta1 0.935 0.188 0.566 0.932 1.313 1.001 4000
beta2 0.425 0.145 0.140 0.425 0.721 1.005 340
mu.c[1] 1508.361 116.760 1292.926 1500.272 1751.959 1.003 550
mu.c[2] 3914.679 821.327 2571.825 3826.222 5785.642 1.002 1300
mu.e[1] 1.584 0.021 1.543 1.584 1.625 1.001 2100
mu.e[2] 1.568 0.033 1.501 1.569 1.632 1.001 4000
mustar.e[1] 1.416 0.021 1.375 1.416 1.457 1.001 2000
mustar.e[2] 1.432 0.033 1.368 1.431 1.499 1.001 4000
nu.c[1] 1.826 0.239 1.390 1.815 2.325 1.001 4000
nu.c[2] 1.146 0.178 0.830 1.140 1.520 1.001 4000
nu.e[1] 47.151 6.796 34.720 46.919 61.105 1.002 3500
nu.e[2] 29.759 5.109 20.548 29.521 40.249 1.001 2600
deviance 2787.318 5.090 2779.520 2786.694 2798.832 1.001 4000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule: pV = var(deviance)/2)
pV = 13.0 and DIC = 2800.3
DIC is an estimate of expected predictive error (lower deviance is better).Model comparison — 10TT
Normal/Normal independent Normal/Normal MCF Gamma/Gamma MCF
Gamma vs log-Normal
Model selection
- So which is the “best” model?…
Warning
All models are wrong… but some are helpful!
George Box
- Neither of the models we’ve tested will be the “truth” — but we want to be able to select the one that fits the data best
- Account for overfitting!
- ONE possible way to do so is to use Information criteria \(\Rightarrow\) DIC
Deviance Information Criterion (DIC)
Original formulation (Spiegelhalter et al, 2002)
\[\displaystyle\dic=p_D + \overline{D(\bm\theta)} = D(\overline{\bm\theta})+2p_d,\] where
\(\class{myblue}{\displaystyle\overline{D(\bm\theta)} =\E\left[D(\bm\theta)\right] = \int -2\log\mathcal{L}(\bm\theta\mid\bm{y})p(\bm\theta\mid\bm{y})d\bm\theta \approx \frac{1}{S}\sum_{s=1}^S -2\log \mathcal{L}(\bm\theta^{(s)})} =\) average model deviance
\(\class{myblue}{\displaystyle D(\overline{\bm\theta})=D(\E\left[\bm\theta\mid\bm{y}\right]) = -2\log\mathcal{L}\left(\int \bm\theta p(\bm\theta\mid\bm{y})d\bm\theta \right) \approx -2\log \mathcal{L} \left( \frac{1}{S}\sum_{s=1}^S \bm\theta^{(s)} \right)}=\) model deviance calculated in correspondence of the average value of the model parameters
\(\class{myblue}{\displaystyle p_D=\overline{D(\bm\theta)}-D(\overline{\bm\theta})}=\) penalty for model complexity
Alternative version (Gelman et al, 2013)
\[\class{myblue}{p_V=\frac{1}{2}\var\left[D(\bm\theta)\right]}\]
10TT — Model selection
| Model | \(p_V\) | \(\dic\)a | \(p_D\) | \(\dic\)b |
|---|---|---|---|---|
| a Computed as \(p_V+\overline{D(\bm\theta)}\) | ||||
| b Computed as \(p_D+\overline{D(\bm\theta)}\) | ||||
| Normal/Normal independent | 76.71 | 3140 | 7.14 | 3070 |
| Normal/Normal MCF | 75.50 | 3136 | 6.90 | 3068 |
| Gamma/Gamma MCF | 12.96 | 2800 | 10.93 | 2798 |
Both versions of the DIC favour the Gamma/Gamma MCF and suggest the two Normal/Normal models are basically indistinguishible
\(p_V\) for the two Normal/Normal models computed as much larger than for the Gamma/Gamma MCF
\(p_D\) has a nice interpretation as effective number of model parameters — more on this later
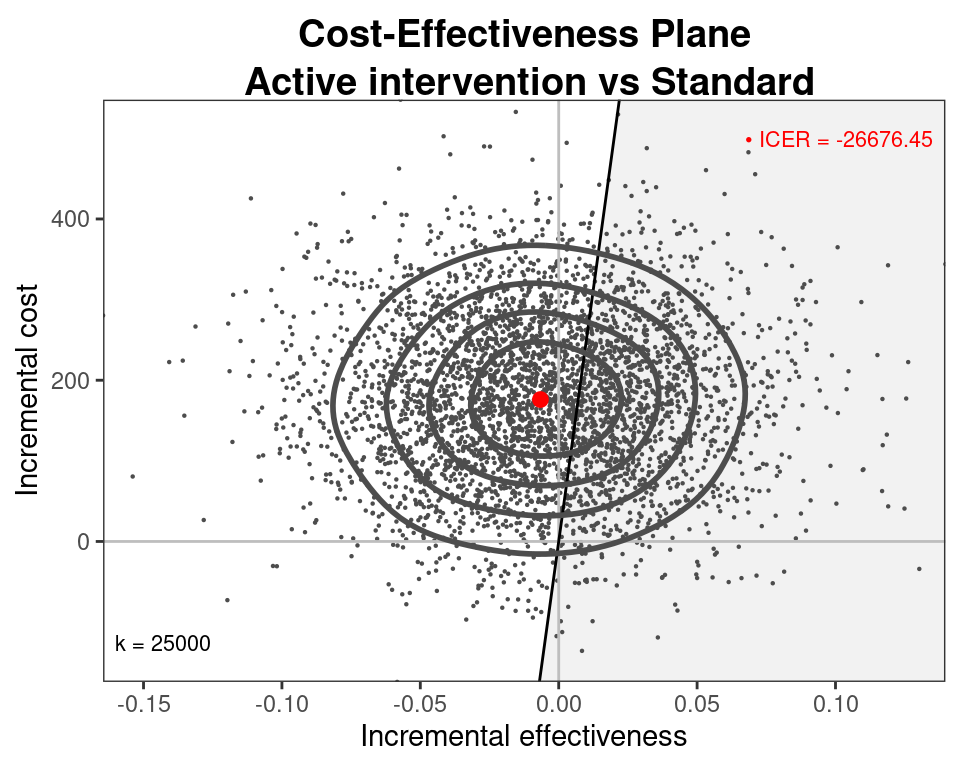
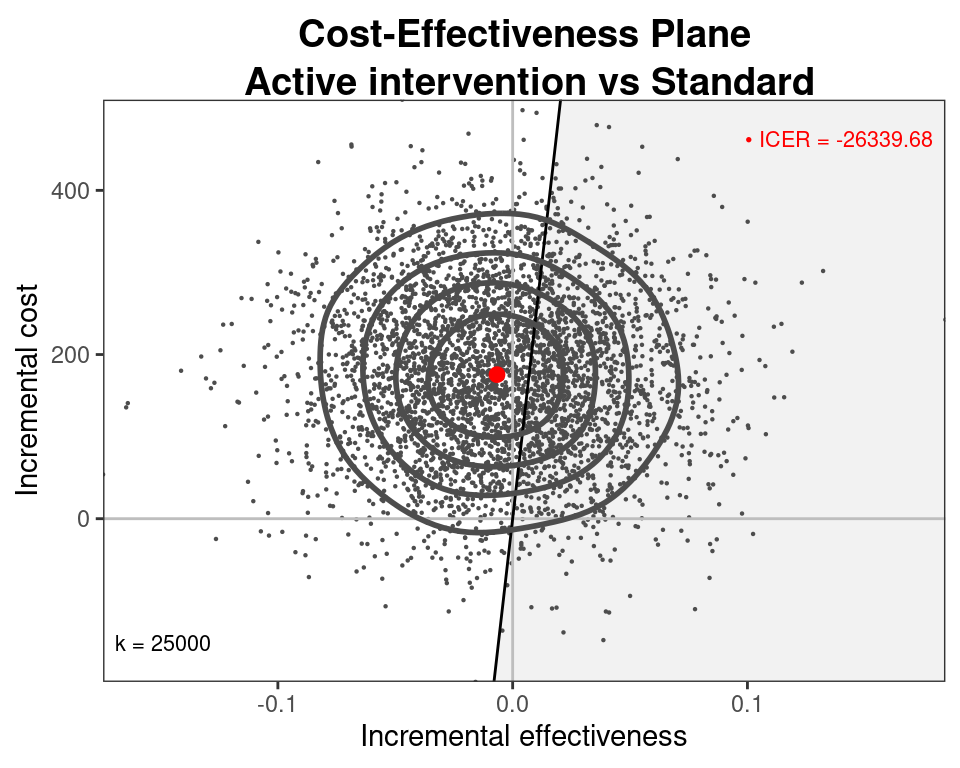
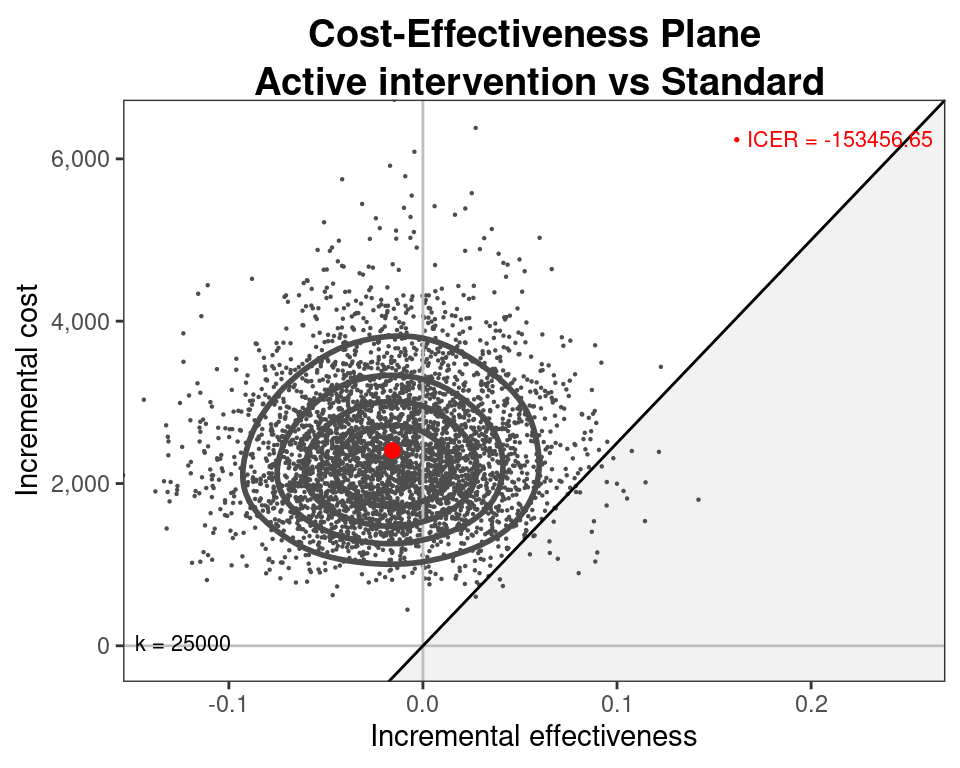
Cost-effectiveness model
- Can use the simulations from the three models for \((\mu_e,\mu_c)\) and then run
BCEAto obtain the economic analysis
1. Intro HTA 2. Bayesian computation 3. ILD 4. ALD 5. NMA © Gianluca Baio (UCL) | | Bayesian models in HTA | VIBASS7 2024 | 10 - 11 July 2024 |