| Placebo | Magnesium | |||||
|---|---|---|---|---|---|---|
| ID | Name | Year | Deaths \((r_1)\) | Total \((n_1)\) | Deaths \((r_2)\) | Total \((n_2)\) |
| 1 | Morton | 1984 | 2 | 36 | 1 | 40 |
| 2 | Rasmussen | 1986 | 23 | 135 | 9 | 135 |
| 3 | Smith | 1986 | 7 | 200 | 2 | 200 |
| 4 | Abraham | 1987 | 1 | 46 | 1 | 48 |
| 5 | Felstedt | 1988 | 8 | 148 | 10 | 150 |
| 6 | Shechter | 1989 | 9 | 56 | 1 | 59 |
| 7 | Ceremuzynski | 1989 | 3 | 23 | 1 | 25 |
| 8 | Bertschat | 1989 | 1 | 21 | 0 | 22 |
| 9 | Singh | 1990 | 11 | 75 | 6 | 76 |
| 10 | Pereira | 1990 | 7 | 27 | 1 | 27 |
| 11 | Shechter 1 | 1991 | 12 | 80 | 2 | 89 |
| 12 | Golf | 1991 | 13 | 33 | 5 | 23 |
| 13 | Thorgersen | 1991 | 8 | 122 | 4 | 130 |
| 14 | LIMIT-2 | 1992 | 118 | 1157 | 90 | 1159 |
| 15 | Shechter 2 | 1995 | 17 | 108 | 4 | 107 |
| 16 | ISIS-4 | 1995 | 2103 | 29039 | 2216 | 29011 |
4. Aggregated level data and evidence synthesis
Gianluca Baio
Department of Statistical Science | University College London
https://gianluca.statistica.it
https://egon.stats.ucl.ac.uk/research/statistics-health-economics
https://github.com/giabaio https://github.com/StatisticsHealthEconomics
@gianlubaio@mas.to @gianlubaio
Bayesian modelling for economic evaluation of healthcare interventions
València International Bayesian Analysis Summer School, 7th edition, University of Valencia
10 - 11 July 2024
Check out our departmental podcast “Random Talks” on Soundcloud!
Follow our departmental social media accounts + magazine “Sample Space”
Summary
- Role of evidence synthesis in decision modelling
- Absolute and relative effects
- Meta-analysis of aggregated summaries from RCTs
- Multi-level hierarchical models
- Exchangeability: No/Partial/Complete pooling
- Magnesium example
- Evidence synthesis in health economics
- Influenza example
References
- The
BUGSBook, chapter 10 - Bayesian Methods in Health Economics, chapter 5.3
- NICE DSU Evidence Synthesis Technical Support Document Series
- Evidence Synthesis for Decision Making in Healthcare
- Data Analysis Using Regression and Multilevel/Hierarchical Models
Evidence-based decisions
- Robust healthcare decisions should:
- Consider all costs and benefits over a patients lifetime
- Be evidence-based, reflecting all relevant evidence
- Economic evaluation based on individual level data from a single RCT
- May not capture longer-term costs/benefits
- May not generalise to other populations/settings
- May not be the only relevant source of evidence… results may differ if we use another source
- Need to identify all relevant evidence
- Transparent, reproducible, specific
- Systematic review
- Population (including subgroups)
- Interventions
- Comparators
- Outcomes
Absolute vs Relative effects
- Absolute effects
- e.g. probabilities, mean scores, event rates
- Typically whats needed in a decision model
- Relative effects
- e.g. log-odds ratio, mean difference, hazard ratio
- By design RCTs provide evidence on relative effects
- \(\ldots\) relative effects more generalisable than the absolute effects
Goal: Apply relative effects to reference absolute effect to obtain absolute effects
- mean\(_1\) = mean\(_0\) + mean difference
- log-odds\(_1\) = log-odds\(_0\) + log OR — equivalently: \(\logit(p_1)=\logit(p_0)+\txt{log OR}\)
- Transforms from log OR \(\mu\) to probability \(p\), using inverse logit function
\[\class{myblue}{p= \displaystyle\frac{\exp(\mu)}{1+\exp(\mu)} \iff \mu = \logit(p) = \log\left(\frac{p}{1-p}\right)}\]
- log-hazard\(_1\) = log-hazard\(_0\) + log HR
NB: we need to fully propagate the uncertainty in the relative to the absolute effect! (Being Bayesian makes life much easier! 😉)
Example — Magnesium
Example — Magnesium
| Placebo | Magnesium | |||||
|---|---|---|---|---|---|---|
| ID | Name | Year | Deaths \((r_1)\) | Total \((n_1)\) | Deaths \((r_2)\) | Total \((n_2)\) |
| 1 | Morton | 1984 | 2 | 36 | 1 | 40 |
| 2 | Rasmussen | 1986 | 23 | 135 | 9 | 135 |
| 3 | Smith | 1986 | 7 | 200 | 2 | 200 |
| 4 | Abraham | 1987 | 1 | 46 | 1 | 48 |
| 5 | Felstedt | 1988 | 8 | 148 | 10 | 150 |
| 6 | Shechter | 1989 | 9 | 56 | 1 | 59 |
| 7 | Ceremuzynski | 1989 | 3 | 23 | 1 | 25 |
| 8 | Bertschat | 1989 | 1 | 21 | 0 | 22 |
| 9 | Singh | 1990 | 11 | 75 | 6 | 76 |
| 10 | Pereira | 1990 | 7 | 27 | 1 | 27 |
| 11 | Shechter 1 | 1991 | 12 | 80 | 2 | 89 |
| 12 | Golf | 1991 | 13 | 33 | 5 | 23 |
| 13 | Thorgersen | 1991 | 8 | 122 | 4 | 130 |
| 14 | LIMIT-2 | 1992 | 118 | 1157 | 90 | 1159 |
| 15 | Shechter 2 | 1995 | 17 | 108 | 4 | 107 |
| 16 | ISIS-4 | 1995 | 2103 | 29039 | 2216 | 29011 |
Example — Magnesium
| Placebo | Magnesium | |||||
|---|---|---|---|---|---|---|
| ID | Name | Year | Deaths \((r_1)\) | Total \((n_1)\) | Deaths \((r_2)\) | Total \((n_2)\) |
| 1 | Morton | 1984 | 2 | 36 | 1 | 40 |
| 2 | Rasmussen | 1986 | 23 | 135 | 9 | 135 |
| 3 | Smith | 1986 | 7 | 200 | 2 | 200 |
| 4 | Abraham | 1987 | 1 | 46 | 1 | 48 |
| 5 | Felstedt | 1988 | 8 | 148 | 10 | 150 |
| 6 | Shechter | 1989 | 9 | 56 | 1 | 59 |
| 7 | Ceremuzynski | 1989 | 3 | 23 | 1 | 25 |
| 8 | Bertschat | 1989 | 1 | 21 | 0 | 22 |
| 9 | Singh | 1990 | 11 | 75 | 6 | 76 |
| 10 | Pereira | 1990 | 7 | 27 | 1 | 27 |
| 11 | Shechter 1 | 1991 | 12 | 80 | 2 | 89 |
| 12 | Golf | 1991 | 13 | 33 | 5 | 23 |
| 13 | Thorgersen | 1991 | 8 | 122 | 4 | 130 |
| 14 | LIMIT-2 | 1992 | 118 | 1157 | 90 | 1159 |
| 15 | Shechter 2 | 1995 | 17 | 108 | 4 | 107 |
| 16 | ISIS-4 | 1995 | 2103 | 29039 | 2216 | 29011 |
Example — Magnesium
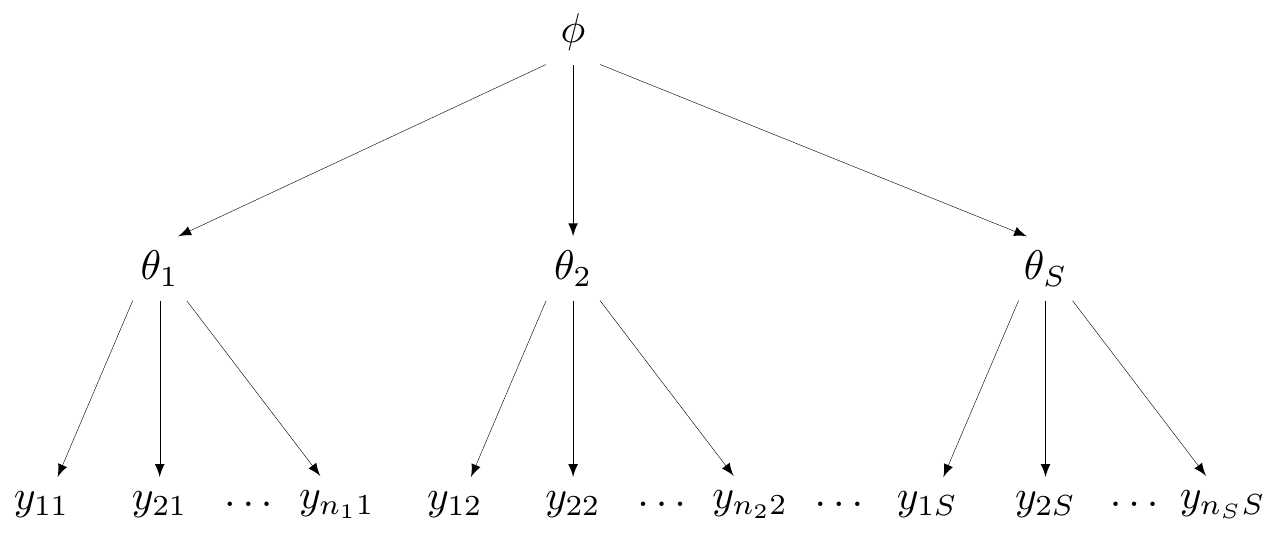
Model
- For study \(i\) in arm \(k\) (for \(k=1\): placebo or \(k=2\): magnesium)
\[\begin{eqnarray*} r_{ik} & \sim & \dbin(\pi_{ik},n_{ik}) \\ \logit(\pi_{ki}) & = & \alpha_i + \delta_i (\text{Trt}_{ik} -1) \end{eqnarray*}\]
- Given this formulation
\[\pi_{ik} = \left\{\begin{array}{ll}\displaystyle \frac{\exp(\alpha_i\,[+\ldots])}{1+\exp(\alpha_i\,[+\ldots])} & \txt{for the placebo arm }(k=1) \\ & \\ \displaystyle \frac{\exp(\alpha_i+\delta_i\,[+\ldots])}{1+\exp(\alpha_i+\delta_i\,[+\ldots])} & \txt{for the magnesium arm } (k=2) \end{array}\right.\]
- Can encode different assumptions on the mechanism for the data generating process
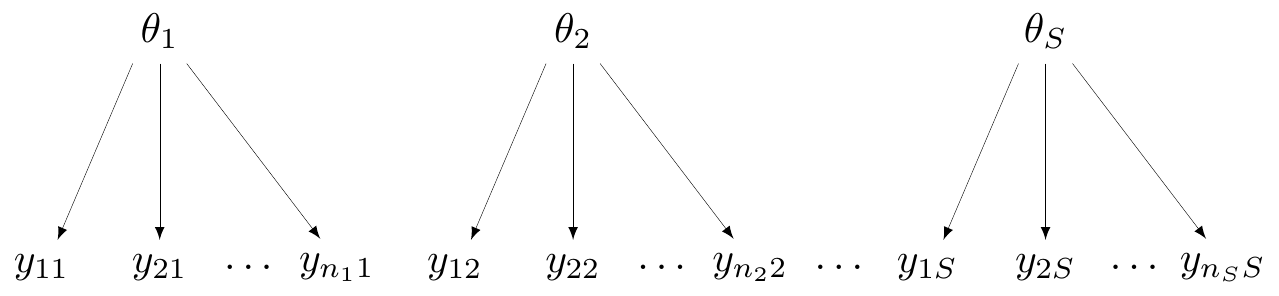
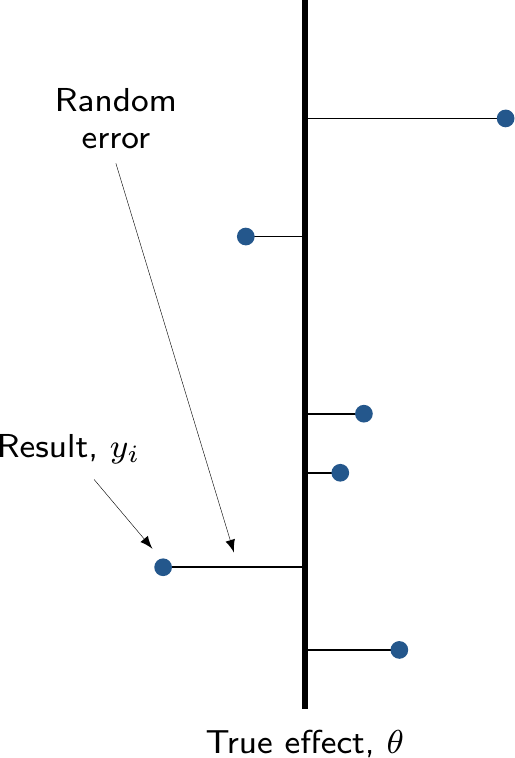
No pooling
- All groups (e.g. “studies”) are assumed independent
- Not much use for economic modelling, unless only a single study is relevant
No pooling
- In Magnesium example, assume \(\alpha_i, \delta_i \stackrel{iid}{\sim}\dnorm(0,sd)\)
NB: \(\pi_i\) is just a logical node and used for ease of notation — but can equivalently write \[\class{myblue}{r_i \sim \dbin({\class{red}{\underbrace{\class{myblue}{\logit^{-1}(\alpha_i + \delta_i \text{Trt}_i)}}_{\pi_i}}},n_i)}\]
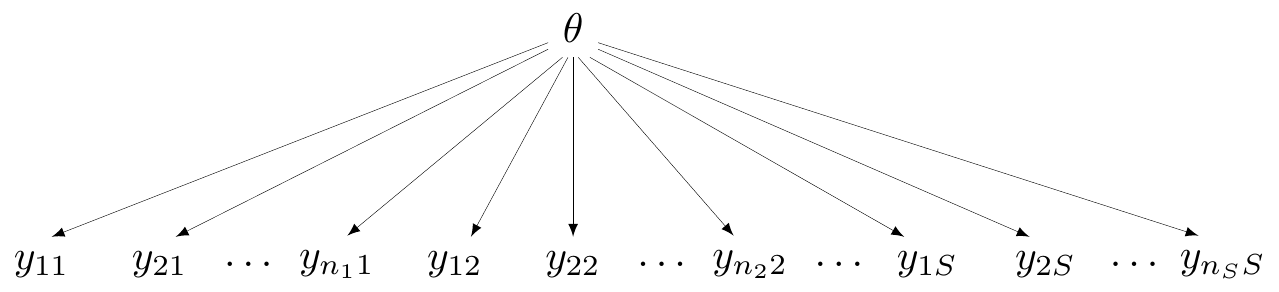
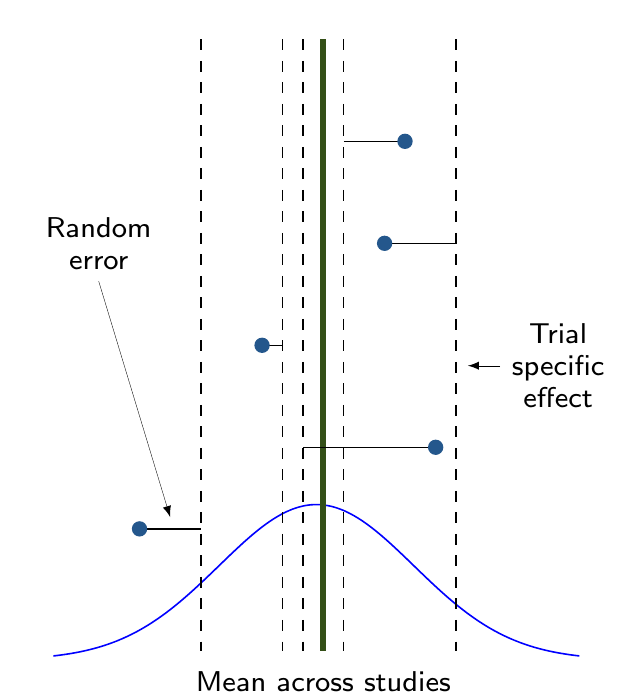
Complete pooling
- Assumes that all studies (and all data points!) are exchangeable
- They are “similar” — all come from the same data generating process
- DGP depends on a single parameter \(\theta\)
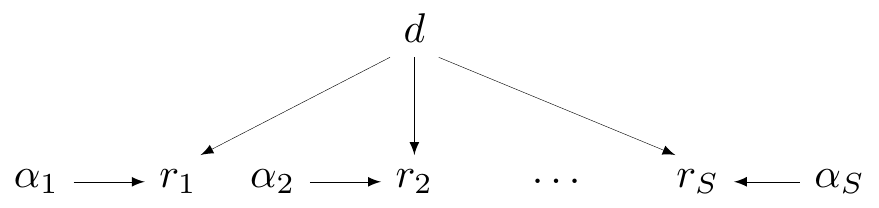
Complete pooling
- In Magnesium example, assume there is a common effect, \(\class{myblue}{\delta_i=d}\) for all \(i=1,\ldots,S\)
Technically, \(\alpha_i\) do vary by study, but they are some kind of “background noise” (the baseline) — the main parameter indicating the treatment effect is the common \(d\)
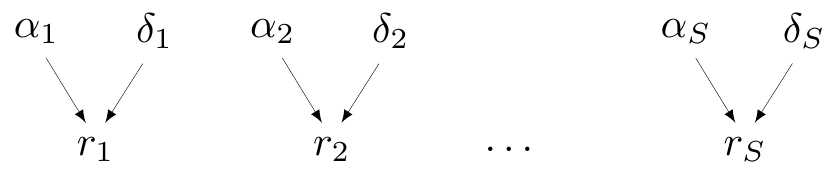
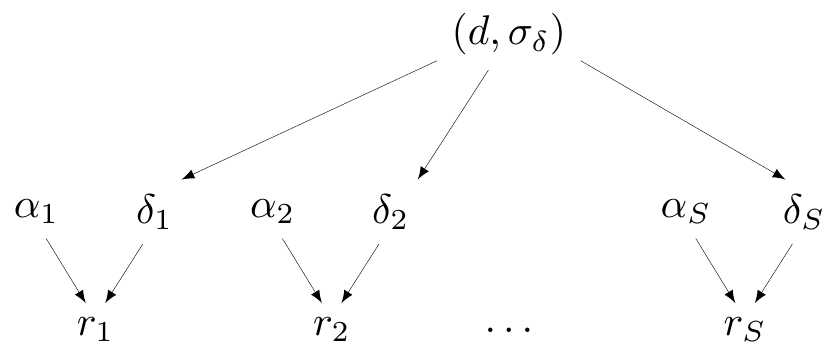
Partial pooling (hierarchical models)
- Data contribute to individual group estimate, but also to overall (pooled) estimate
Partial pooling (hierarchical models)
- In Magnesium example, assume
- \(\delta_i \sim \dnorm(d,\sigma_\delta)\)
- \(d \sim \dnorm(0,sd)\)
- \(\sigma_\delta \sim p(\sigma_\delta)\)
Complete vs partial pooling
Example — Magnesium
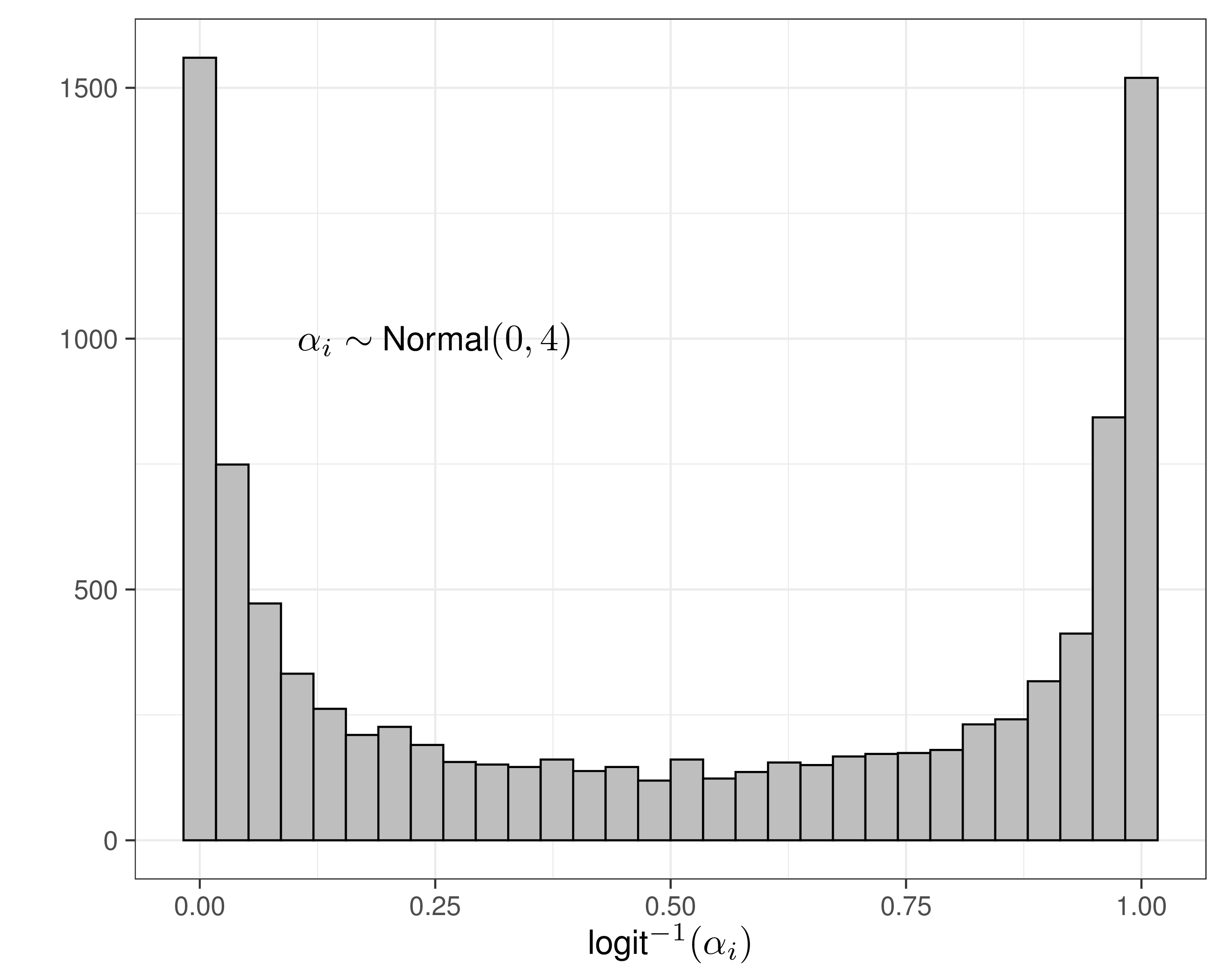
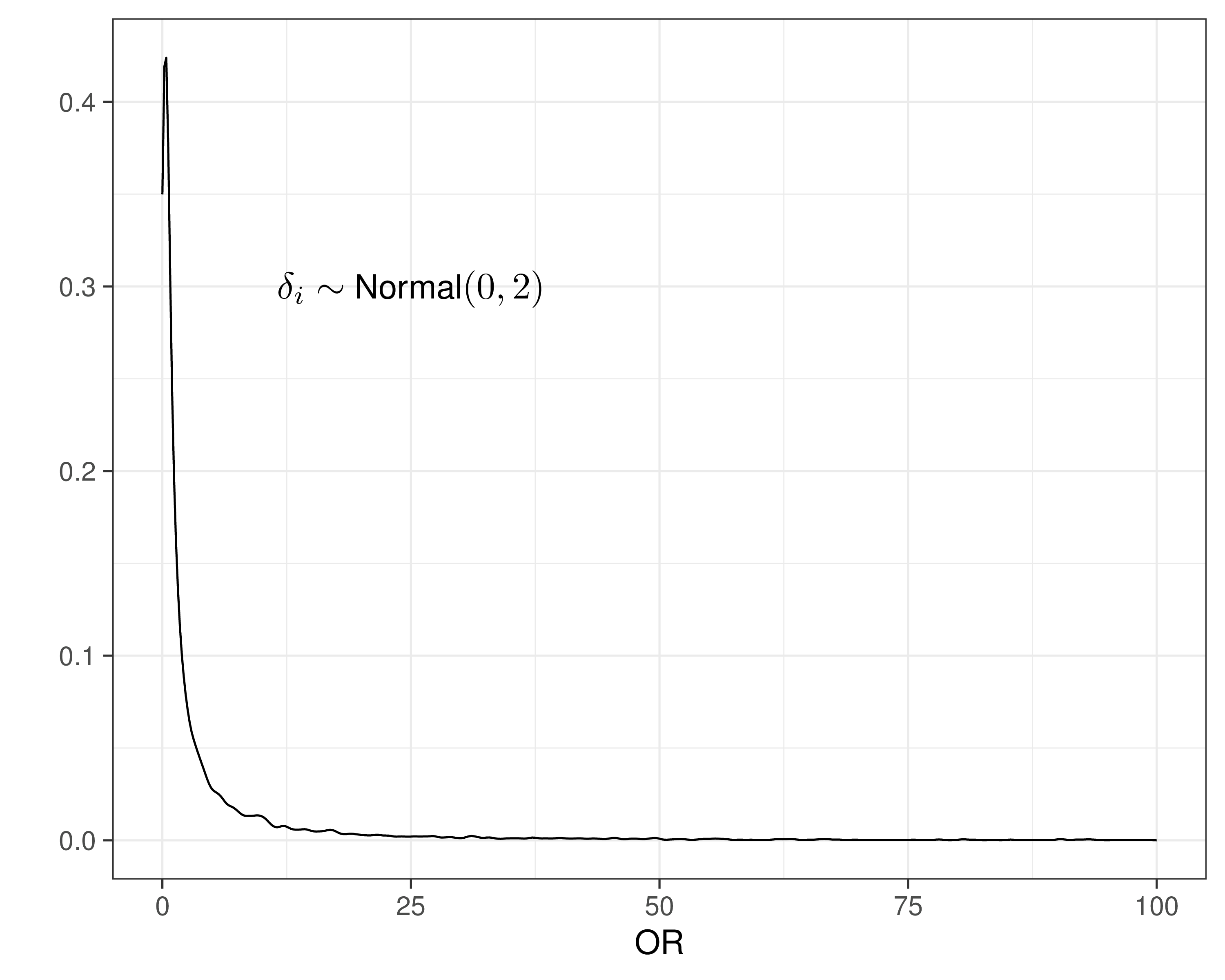
- Need to specify priors for \(\alpha_i,\delta_i\)
- Could assume \(sd \rightarrow \infty\) to ensure “no influence of the prior”…
- That’s overly cautious and unnecessary!
- These are modelled on the logit scale, so can use much smaller values for \(sd\) and still not imply too much information in the prior!
Example — Magnesium
No pooling model
model {
for(i in 1:S) {
# Sampling distributions
r1[i] ~ dbin(pi1[i], n1[i])
r2[i] ~ dbin(pi2[i], n2[i])
# Linear predictors
logit(pi1[i]) <- alpha[i]
logit(pi2[i]) <- alpha[i] + delta[i]
# Baselines (NB: sd=4 => precision = 0.0625)
alpha[i] ~ dnorm(0,0.0625)
# Study-specific treatment effects (sd=2 => precision = 0.25)
delta[i] ~ dnorm(0,0.25)
}
}Example — Magnesium
Partial pooling model
model {
for(i in 1:S) {
# Sampling distributions
r1[i] ~ dbin(pi1[i], n1[i])
r2[i] ~ dbin(pi2[i], n2[i])
# Linear predictors
logit(pi1[i]) <- alpha[i]
logit(pi2[i]) <- alpha[i] + delta[i]
# Baselines (NB: sd=4 => precision = 0.0625)
alpha[i] ~ dnorm(0,0.0625)
# "Random" Effects
delta[i] ~ dnorm(d, prec)
}
# Priors
d ~ dnorm(0,0.25)
# Pr(sigma.delta>1) \approx 0.1
sigma.delta ~ dexp(2.31)
prec <- pow(sigma.delta,-2)
# Summaries
OR <- exp(d)
delta.pred ~ dnorm(d, prec)
}Example — Magnesium
Complete pooling model
model {
for(i in 1:S) {
# Sampling distributions
r1[i] ~ dbin(pi1[i], n1[i])
r2[i] ~ dbin(pi2[i], n2[i])
# Linear predictors
logit(pi1[i]) <- alpha[i]
logit(pi2[i]) <- alpha[i] + delta[i]
# Baselines (NB: sd=4 => precision = 0.0625)
alpha[i] ~ dnorm(0,0.0625)
# "Degenerate Random" Effects
delta[i] ~ dnorm(d, prec)
}
# Priors
d ~ dnorm(0,0.25)
# No variance for the random effects, so not really random...
sigma.delta <- 0
prec <- pow(sigma.delta,-2)
# Summaries
OR <- exp(d)
delta.pred ~ dnorm(d, prec)
}Example — Magnesium
Complete pooling model
Example — Magnesium
Running the models in JAGS
Can use code such as this
# Calls JAGS to run the partial pooling model (others are similar...)
model$partial_pooling=jags(
data=data,
parameters.to.save=c(
"delta","d","delta.pred","OR","sigma.delta","alpha"
),
inits=function(){
list(alpha=rnorm(16),delta=rnorm(16),d=rnorm(1),sigma.delta=runif(1))
},
n.chains=2,
n.iter=10000,
n.burnin=2000,
n.thin=4,
DIC=TRUE,
model.file=partial_pooling,
pD=TRUE
)Example — Magnesium
Running the models in JAGS
Can use code such as this
# Calls JAGS to run the partial pooling model (others are similar...)
model$partial_pooling=jags(
data=data,
parameters.to.save=c(
"delta","d","delta.pred","OR","sigma.delta","alpha"
),
inits=function(){
list(alpha=rnorm(16),delta=rnorm(16),d=rnorm(1),sigma.delta=runif(1))
},
n.chains=2,
n.iter=10000,
n.burnin=2000,
n.thin=4,
DIC=TRUE,
model.file=partial_pooling,
pD=TRUE
)NB: The option pD is only available with the GitHub version of R2jags (though it will be ported to CRAN soon!)
Effective number of model parameters
- Complete pooling (\(\sigma_\delta=0\))
- 16: \(\alpha_i\) study-specific baselines
- 1: \(d\) (common effect)
- 17 total nominal parameters — \(p_D=\) 17.87
- Partial pooling (\(\sigma_\delta>0\))
- 16: \(\alpha_i\) study-specific baselines
- \(\delta_i\) exchangeable (correlated)
- \(p_D=\) 23.73 \(\Rightarrow\) considerable borrowing/shrinkage…
- No pooling (\(\sigma_\delta \rightarrow \infty\))
- 16: \(\alpha_i\) study-specific baselines
- 16: \(\delta_i\) study-specific effects
- 32 total nominal parameters — \(p_D=\) 28.91
Example — Magnesium
Model selection
| Model | \(p_V\) | \(p_D\) | DIC | \(\E\left[D(\bm\theta)\right]\) | \(\sd\left[D(\bm\theta)\right]\) |
|---|---|---|---|---|---|
| No-pooling | 27.69 | 28.91 | 175.79 | 148.10 | 7.46 |
| Complete pooling | 16.91 | 17.87 | 211.89 | 194.98 | 5.84 |
| Partial pooling | 25.42 | 23.73 | 172.58 | 147.16 | 7.13 |
| Model | OR (95% interval) | Between study sd, \(\sigma_\delta\) | \(\overline{D(\bm\theta)}\) | \(p_D\) | DIC |
|---|---|---|---|---|---|
| Complete pooling | 1.01 (0.95; 1.07) | \(-\) | 194.98 | 17.87 | 212.85 |
| Partial pooling | 0.43 (0.26; 0.65) | 0.61 (0.31; 1.04) | 147.16 | 23.73 | 170.89 |
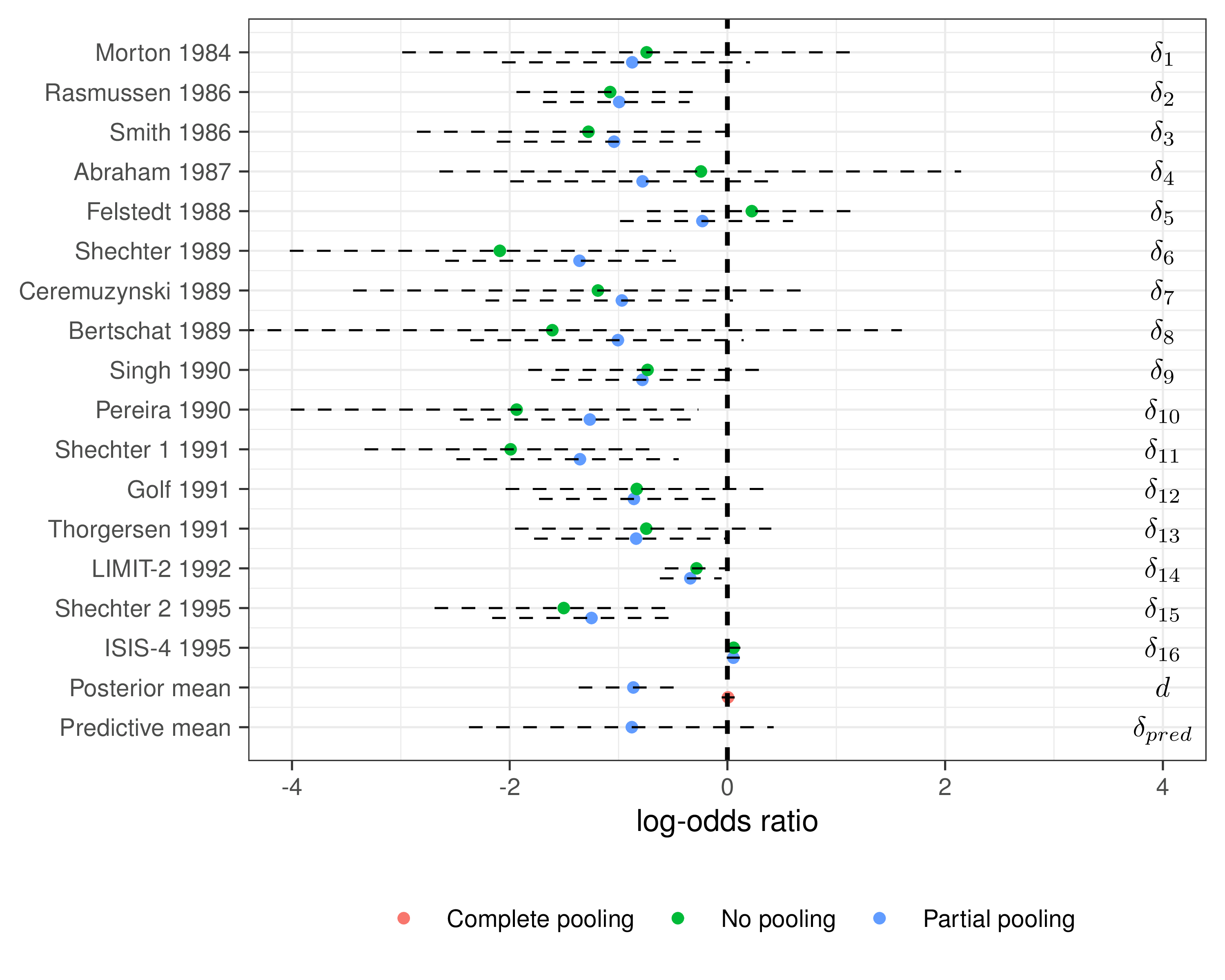
Example — Magnesium
Model comparison
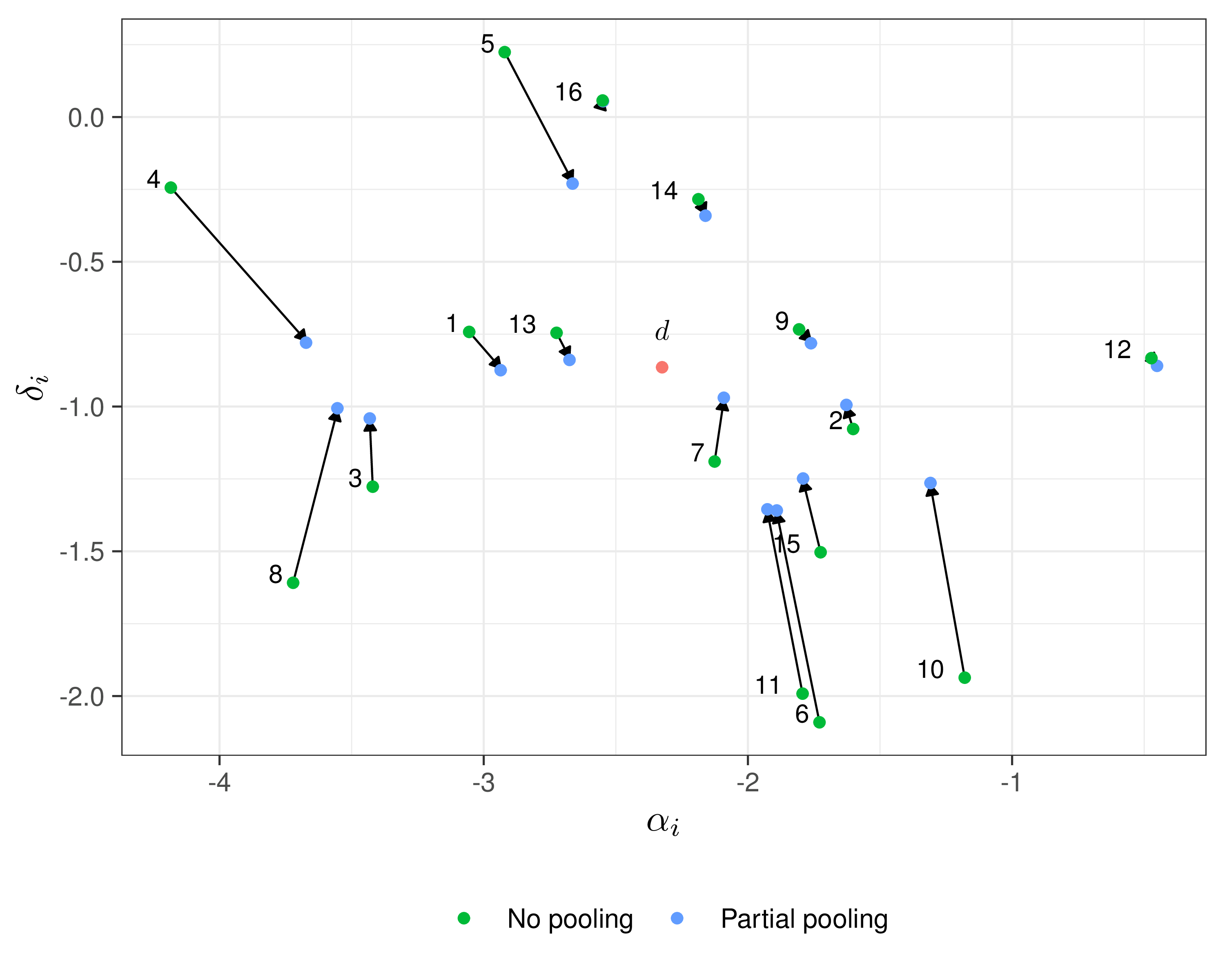
Example — Magnesium
Shrinkage
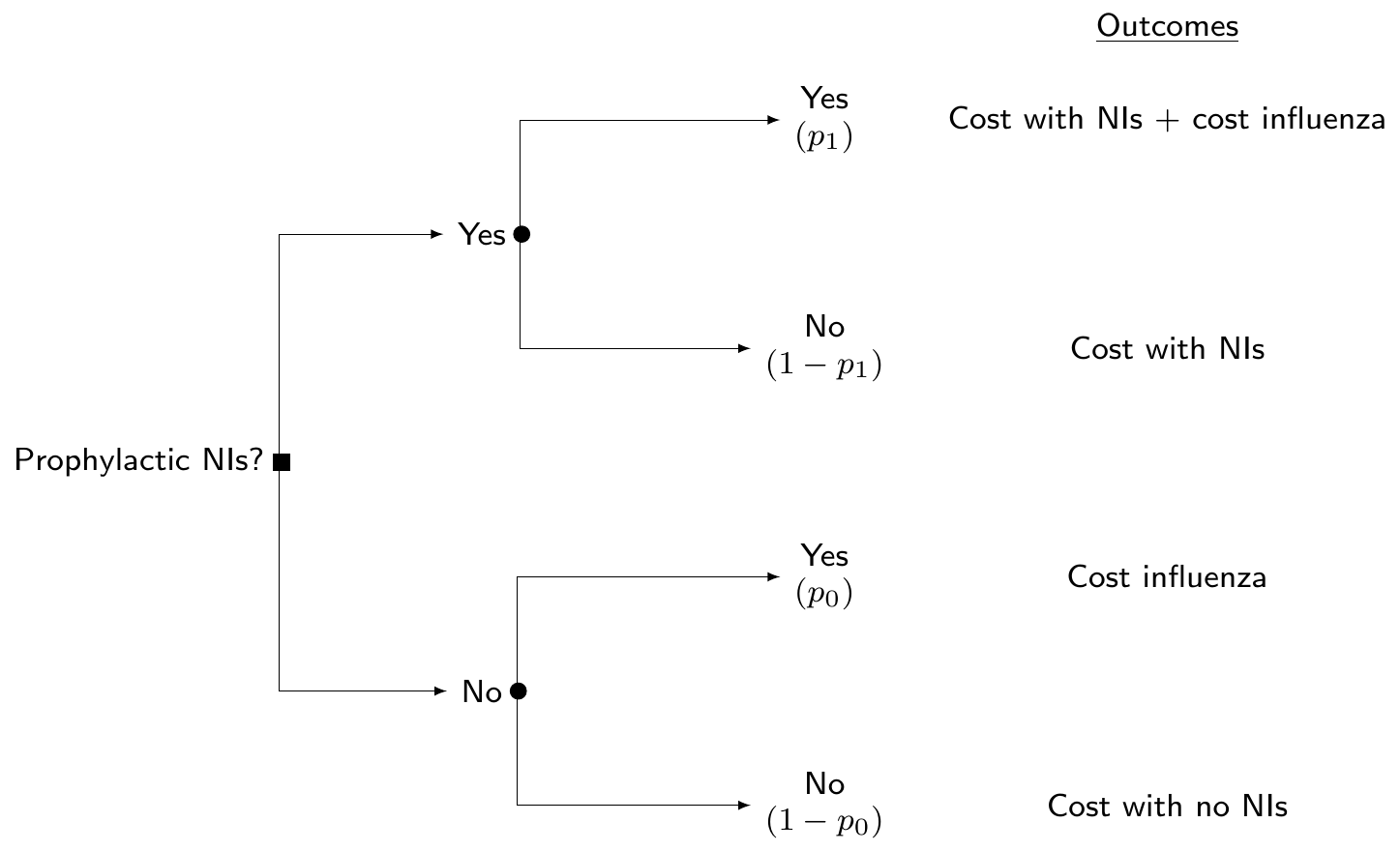
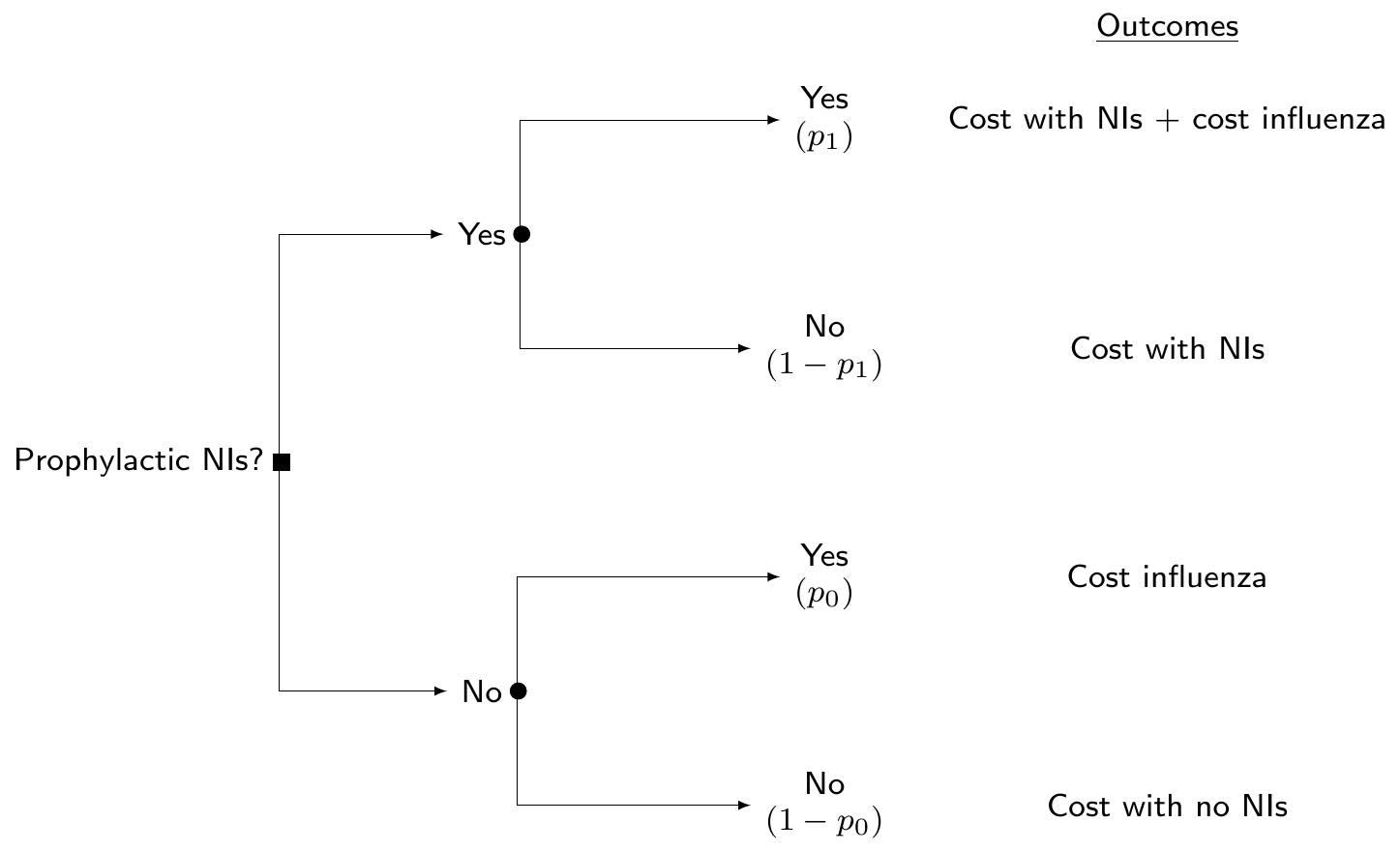
(“Standard”) cost-effectiveness modelling
- Build a population level model (e.g. decision tree or Markov model)
- NB: in this case, the “data” are typically represented by summary statistics for the parameters of interest \(\bm\theta=(p_0,p_1,l,\ldots)\), but may also have access to a combination of ILD and summaries
- Use point estimates for the parameters to build the “base-case” (average) evaluation
- Use resampling methods (eg bootstrap) to propage uncertainty in the point estimates and perform uncertainty analysis
Bayesian cost-effectiveness modelling
- Build a population level model (e.g. decision tree or Markov model)
- NB: in this case, the “data” are typically represented by summary statistics for the parameters of interest \(\bm\theta=(p_0,p_1,l,\ldots)\), but may also have access to a combination of ILD and summaries
- Estimate all model parameters at once and obtain MCMC simulations to run PSA and decision analysis at once
Cost-effectiveness analysis
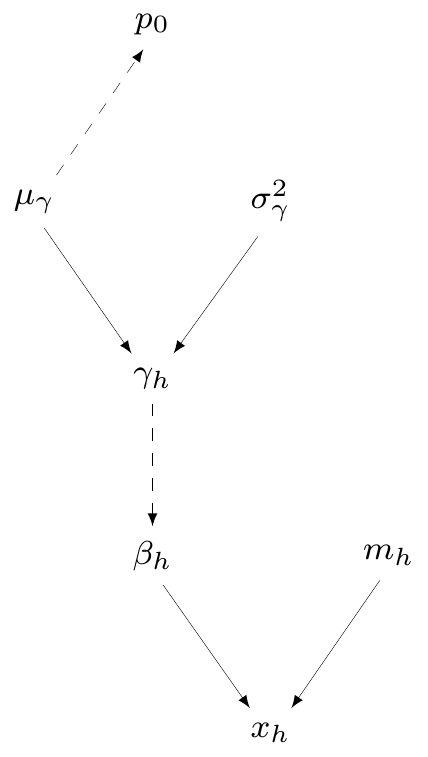
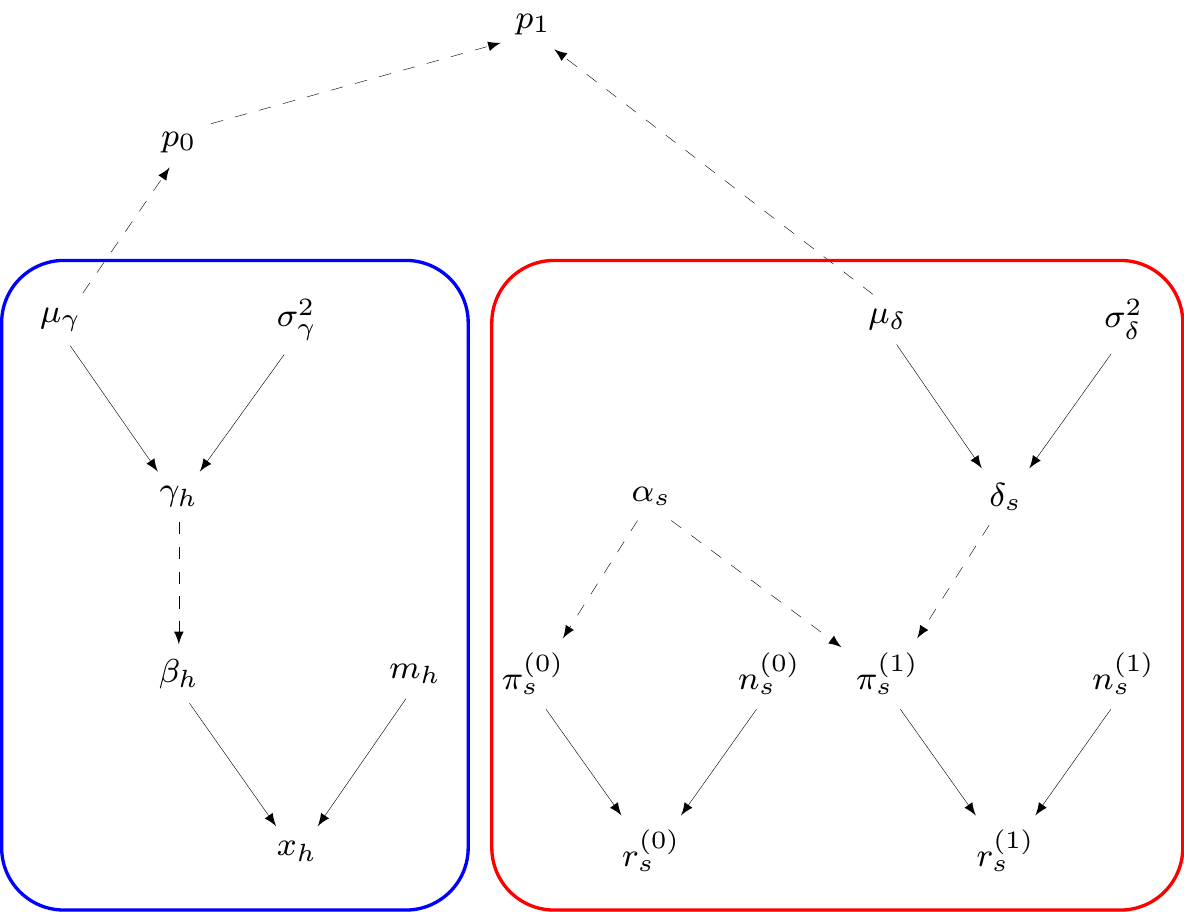
Module 1: Influenza incidence
\(H\) studies reporting number of patients who get influenza (\(x_h\)) in the sample (\(m_h\))
\(\beta_h=\) population probability of influenza from the \(h\)-th study: \(\logit(\beta_h)=\gamma_h\sim \dnorm(\mu\gamma,\sigma_\gamma)\)
\(\mu_\gamma\sim\dnorm(0,v)\) \(=\) pooled averaged probability of infection (on logit scale!) \(\Rightarrow \displaystyle \class{red}{p_0=\frac{\exp(\mu_\gamma)}{1+\exp(\mu_\gamma)}}\)
— or equivalently \(\class{red}{\logit(p_0)=\mu_\gamma}\)
Cost-effectiveness analysis
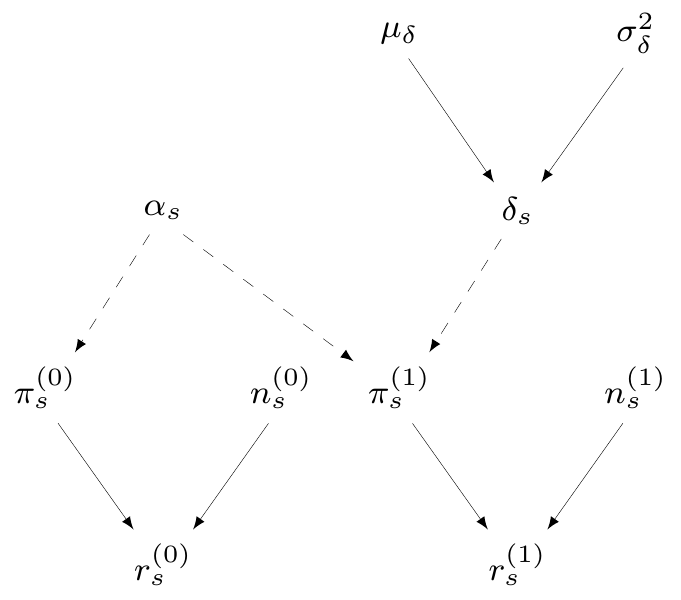
Module 2: Prophylaxis effectiveness
\(S\) studies reporting number of infected patients \(r^{(t)}_s\) in a sample made of \(n^{(t)}_s\) subjects
\(\pi^{(t)}_s=\) study- and treatment-specific chance of contracting influenza
\(\logit\left(\pi^{(0)}_s\right) = \alpha_s \sim \dnorm(0, 10)\)
\(\logit\left(\pi^{(1)}_s\right) = \alpha_s + \delta_s\)
\(\delta_s \sim \dnorm(\mu_\delta,\sigma_\delta)=\) study-specific treatment effect
\(\class{blue}{\mu_\delta\sim\dnorm(0,v)}=\) pooled log-odds ratio of influenza given treatment
Cost-effectiveness analysis
Decision analytic model
Can combine modules 1 and 2 to get \(\class{olive}{\logit(p_1)=\logit(p_0)+\mu_\delta}\)
Cost-effectiveness analysis
Model code
model {
# Evidence synthesis on incidence of influenza in the "healthy" adults population (t=0)
for (h in 1:H) {
x[h] ~ dbin(beta[h], m[h])
logit(beta[h]) <- gamma[h]
gamma[h] ~ dnorm(mu.gamma, tau.gamma)
}
# Evidence synthesis for effectiveness of NIs (t=1 vs t=0)
for (s in 1:S) {
r0[s] ~ dbin(pi0[s], n0[s])
r1[s] ~ dbin(pi1[s], n1[s])
logit(pi0[s]) <- alpha[s]
logit(pi1[s]) <- alpha[s]+delta[s]
# Partial pooling on the treatment effect delta[s]
delta[s] ~ dnorm(mu.delta,tau.delta)
alpha[s] ~ dnorm(0,0.00001)
}
# Prior distributions
mu.delta ~ dnorm(0,0.00001); mu.gamma ~ dnorm(0,0.00001)
sigma.delta ~ dunif(0,10); tau.delta <- pow(sigma.delta,-2)
sigma.gamma ~ dunif(0,10); tau.gamma <- pow(sigma.gamma,-2)
# Costs of influenza
c.inf ~ dnorm(mu.inf,tau.inf)
# Length of time to recovery when infected by influenza
l ~ dlnorm(mu.l,tau.l)
# Odds Ratio of influenza under treatment with NIs
rho <- exp(mu.delta)
# Estimated probability of influenza in "healthy adults" for t=0
logit(p0) <- mu.gamma
# Estimated probability of influenza in "healthy adults" for t=1
logit(p1) <- mu.gamma + mu.delta
}Cost-effectiveness analysis
Model fitting
# Defines the parameters list
parameters <- c("p0","p1","l","c.inf","rho")
# Creates a function to draw random initial values
inits <- function(){
list(alpha=rnorm(S,0,1), delta=rnorm(S,0,1), mu.delta=rnorm(1),
sigma.delta=runif(1), gamma=rnorm(H,0,1), mu.gamma=rnorm(1),
sigma.gamma=runif(1), c.inf=rnorm(1))
}
# Sets the number of iterations, burnin and thinning
n.iter <- 10000
n.burnin <- 5000
n.thin <- 10
# Finally calls JAGS to do the MCMC run and saves results to the object "model"
model <- jags(data=data,inits=inits,parameters.to.save=parameters,model.file=model.code,
n.chains=2, n.iter, n.burnin, n.thin, DIC=TRUE)
# Prints the model summaries
print(model,digits=3,intervals=c(.025,.975))Inference for Bugs model at "/tmp/Rtmp5py8EG/model1b7ea54537fd0.txt",
2 chains, each with 10000 iterations (first 5000 discarded), n.thin = 10
n.sims = 1000 iterations saved. Running time = 0.292 secs
mu.vect sd.vect 2.5% 97.5% Rhat n.eff
c.inf 16.871 2.308 12.439 21.274 1.001 1000
l 8.177 1.377 5.752 11.186 1.002 890
p0 0.059 0.021 0.026 0.103 1.000 1000
p1 0.013 0.008 0.004 0.032 1.000 1000
rho 0.213 0.083 0.096 0.422 1.000 1000
deviance 101.934 5.860 91.986 115.269 1.002 910
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule: pV = var(deviance)/2)
pV = 17.2 and DIC = 119.1
DIC is an estimate of expected predictive error (lower deviance is better).Cost-effectiveness analysis
Economic modelling
- \(l\) proxy for QALY loss due to influenza (length of time to recovery)
- NB: GP cost incurred under all options, and so could be omitted from model…
Cost-effectiveness analysis
Decision analysis
# Loads the BCEA package to post-process the model output into the economic evaluation
library(BCEA)
# Defines treatment labels
trt.labels=c("status quo","prophylaxis with NIs")
# Runs the 'bcea' function to create the economic output
m <- bcea(e,c,ref=2,interventions=trt.labels,Kmax=10000)
# Summarises the results
summary(m)NB: k (wtp) is defined in the interval [0 - 10000]
Cost-effectiveness analysis summary
Reference intervention: prophylaxis with NIs
Comparator intervention: status quo
Optimal decision: choose status quo for k < 60 and prophylaxis with NIs for k >= 60
Analysis for willingness to pay parameter k = 10000
Expected net benefit
status quo -4876.5
prophylaxis with NIs -1133.1
EIB CEAC ICER
prophylaxis with NIs vs status quo 3743.3 1 42.953
Optimal intervention (max expected net benefit) for k = 10000: prophylaxis with NIs
EVPI 4.3707e-141. Intro HTA 2. Bayesian computation 3. ILD 4. ALD 5. NMA © Gianluca Baio (UCL) | | Bayesian models in HTA | VIBASS7 2024 | 10 - 11 July 2024 |