1. Introduction to health economic evaluation


Gianluca Baio

Department of Statistical Science   |   University College London

g.baio@ucl.ac.uk


https://gianluca.statistica.it

https://egon.stats.ucl.ac.uk/research/statistics-health-economics

https://github.com/giabaio   https://github.com/StatisticsHealthEconomics  

@gianlubaio@mas.to     @gianlubaio    


Bayesian modelling for economic evaluation of healthcare interventions

València International Bayesian Analysis Summer School, 7th edition, University of Valencia

10 - 11 July 2024

Check out our departmental podcast “Random Talks” on Soundcloud!

Follow our departmental social media accounts + magazine “Sample Space”

Disclaimer…

… Just so you know what you’re about to get yourself into… 😉

Summary

  • Health economic evaluation
    • What is and why do we need health economics?
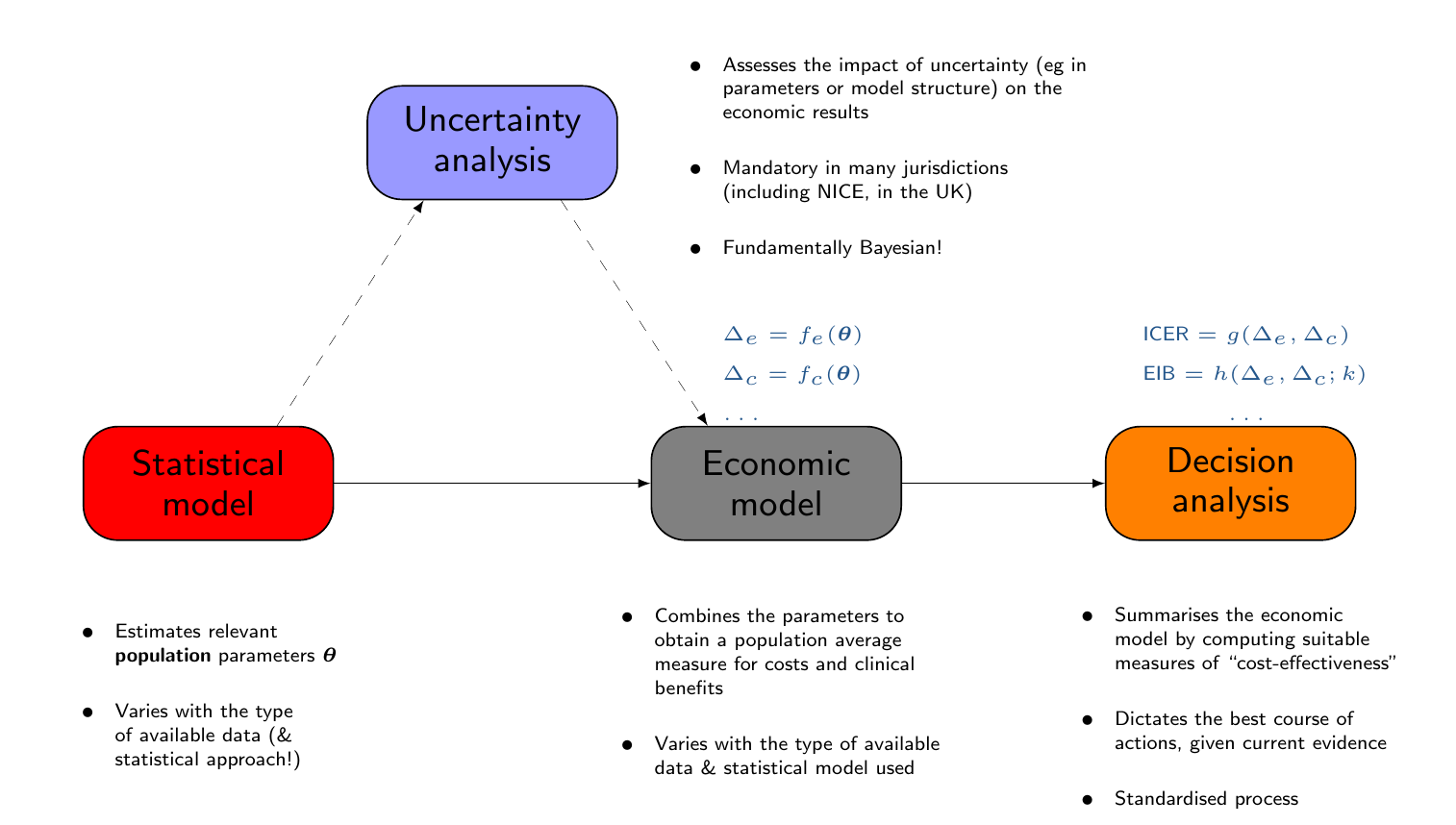
  • A framework for health economic evaluation
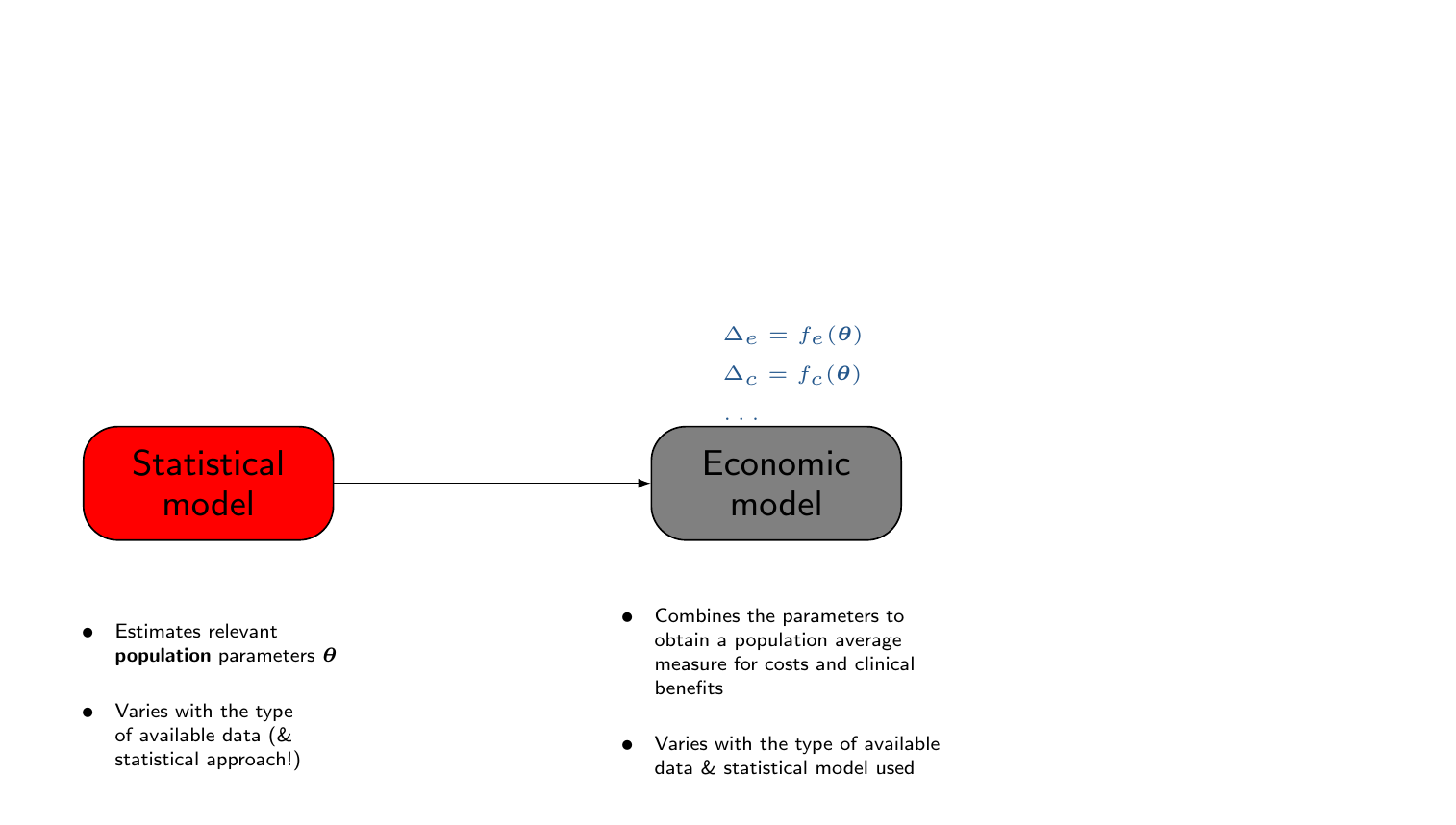
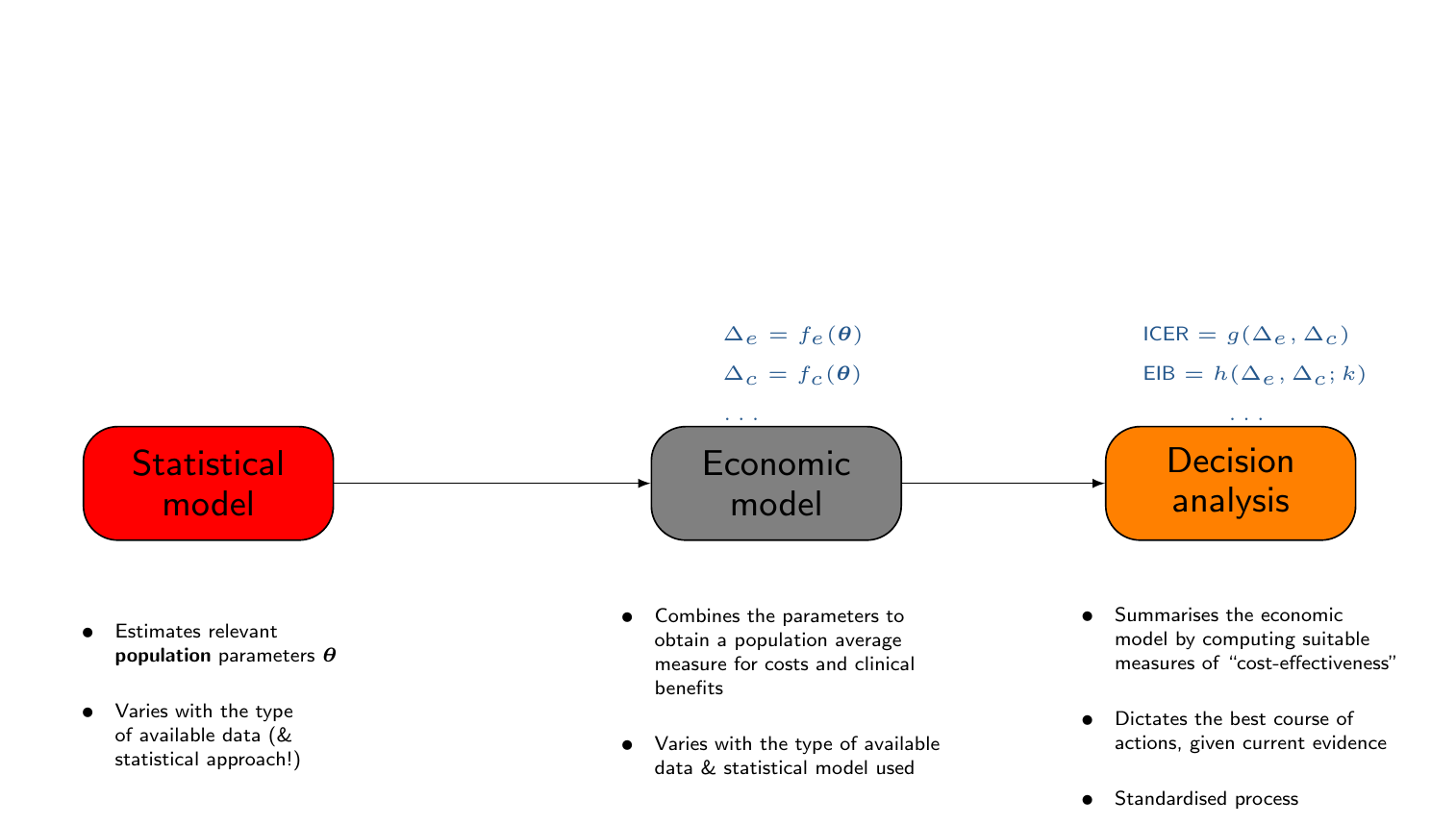
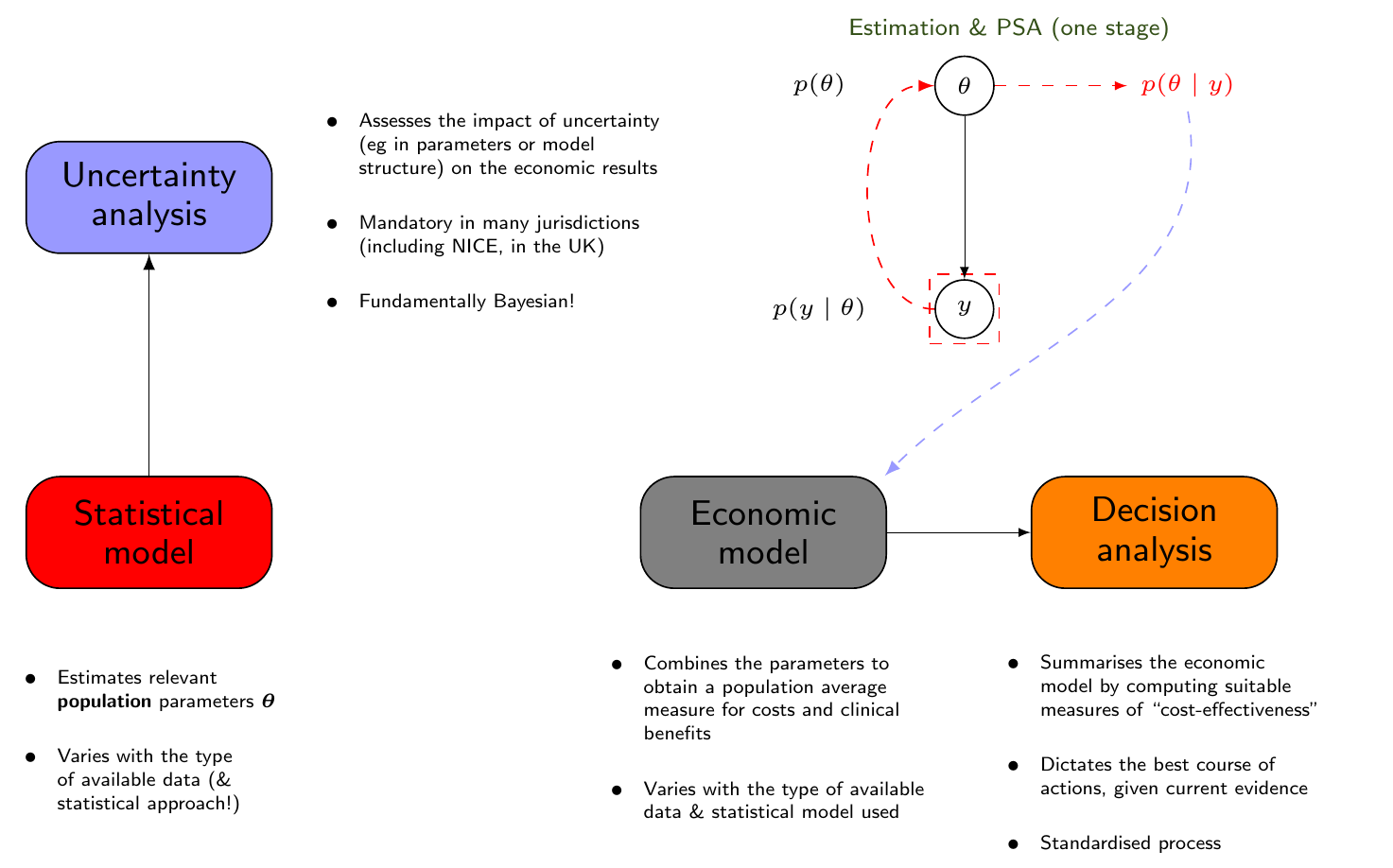
    • Statistical modelling
    • Economic modelling
    • Decision analysis
    • Uncertainty analysis
  • Standard vs Bayesian HTA
    • Two-stage vs integrated approach
  • Decision-making
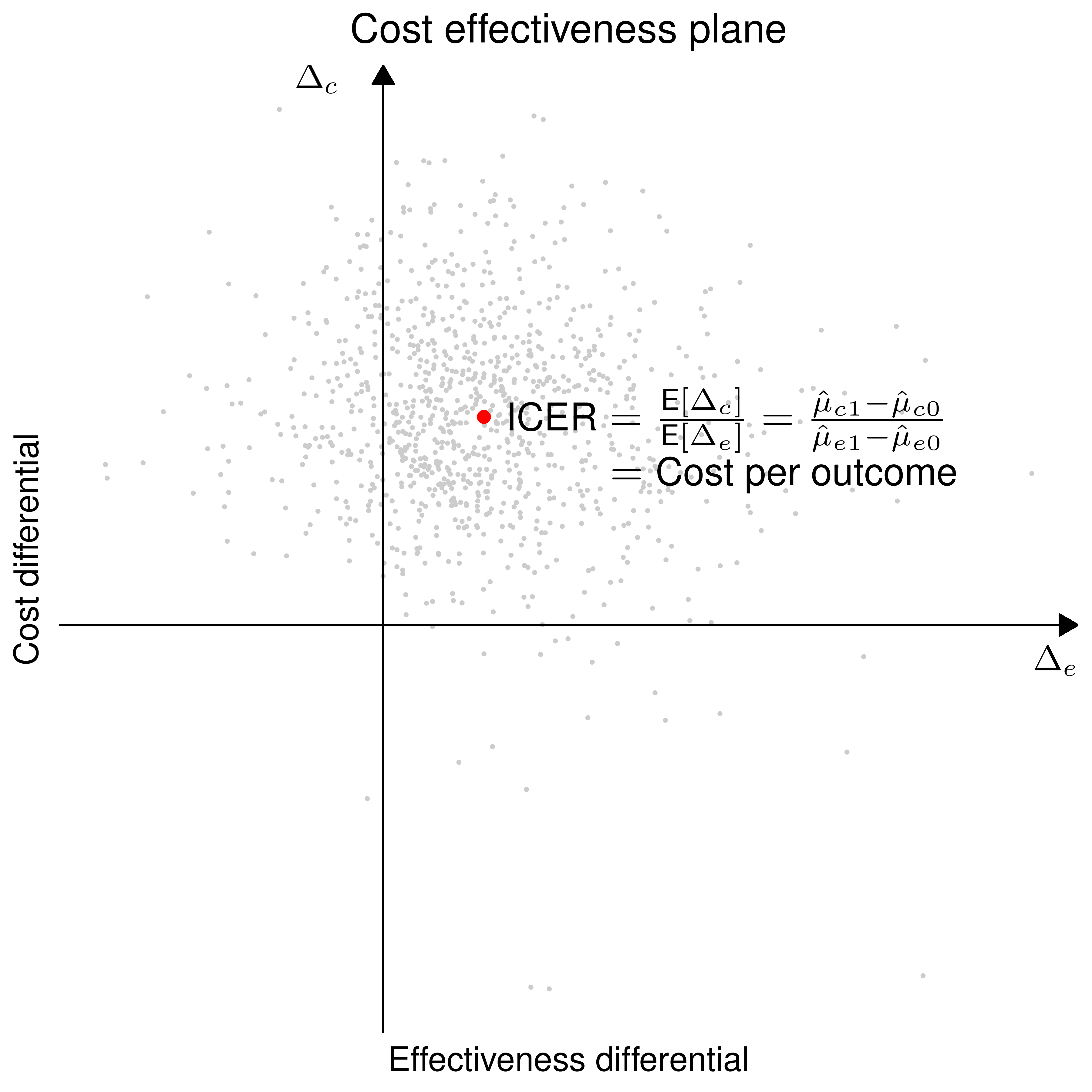
    • Cost-effectiveness plane; ICER; EIB

References

Health technology assessment (HTA)

Objective

  • Combine costs and benefits of a given intervention into a rational scheme for allocating resources

Health technology assessment (HTA) is a method of evidence synthesis that considers evidence regarding clinical effectiveness, safety, cost-effectiveness and, when broadly applied, includes social, ethical, and legal aspects of the use of health technologies. The precise balance of these inputs depends on the purpose of each individual HTA. A major use of HTAs is in informing reimbursement and coverage decisions, in which case HTAs should include benefit-harm assessment and economic evaluation. Luce et al, 2010

(Quote stolen from a brilliant presentation by Cynthia Iglesias)

A relatively new discipline

  • Basically becomes “a thing” in the 1970s
  • Arguably, a historical accident…
    • Economists take the lead in developing the main theory \(\Rightarrow\) Health Economics
    • But there’s so much more to it (more on this later…)

(Truly…) World-beating Britain

Health technology assessment (HTA)

Objective

  • Combine costs and benefits of a given intervention into a rational scheme for allocating resources

Health technology assessment (HTA)

Objective

  • Combine costs and benefits of a given intervention into a rational scheme for allocating resources

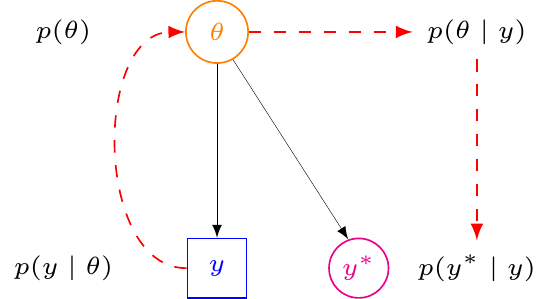
To be or not to be?… (A Bayesian)

Frequentist (“standard”)

Bayesian

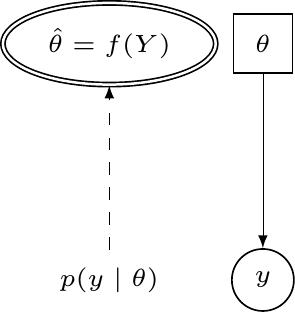
  • A Bayesian only speaks one language: probability distributions to describe
    • Sampling variability (relevant for observed data)
    • Epistemic uncertainty (relevant for unobservable parameters + yet unobserved future data)
  • Contextual (=“prior”) information to be formally included in the construction of the model
    • Almost irrelevant when evidence is “definitive” (large and consistent data)
    • Crucial when data are sparse!

To be or not to be?… (A Bayesian)

In HTA

Frequentist (“standard”)

2./3. Economic modelling+Decision analysis

Base-case scenario

\[\class{myblue}{\Delta_e=}\class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\hat\theta}_1]}}_{\class{red}{\hat\mu_{e1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\hat\theta}_0]}}_{\class{red}{\hat\mu_{e0}}}}\]

\[\class{myblue}{\Delta_c=}\class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\hat\theta}_1]}}_{\class{red}{\hat\mu_{c1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\hat\theta}_0]}}_{\class{red}{\hat\mu_{c0}}}}\]

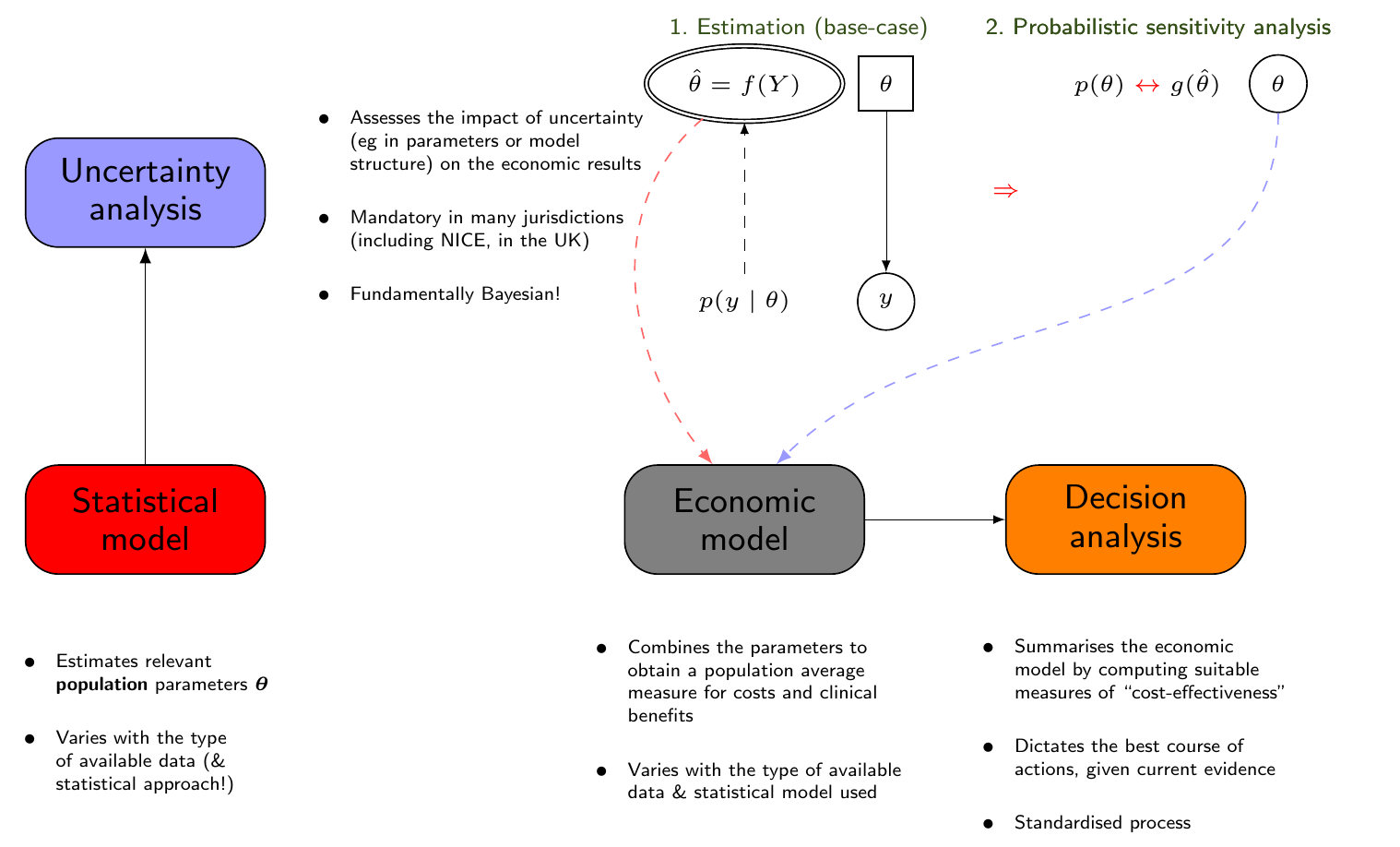
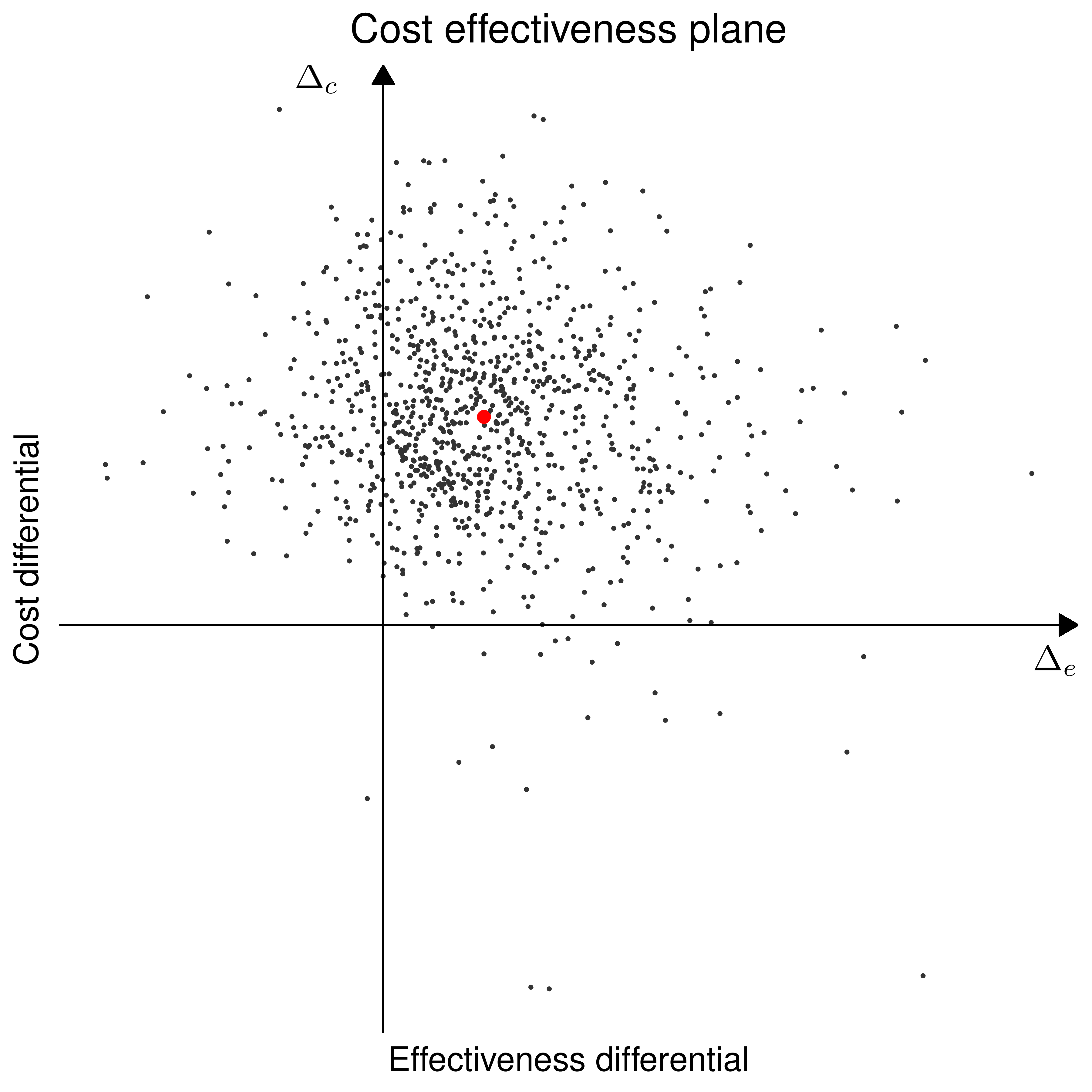
4. Uncertainty analysis

Uncertainty induced by \(g(\boldsymbol{\hat\theta}_0),g(\boldsymbol{\hat\theta}_1)\) — typically independent simulations

Statistical model

Economic model

Status quo

New drug

Decision analysis

Status quo
Benefits Costs
741 670382.1
699 871273.3
... ...
726 425822.2
716.2 790381.2

New drug
Benefits Costs
732 1131978
664 1325654
... ...
811 766411.4
774.5 1066849.8

4. Uncertainty analysis

Uncertainty induced by \(g(\boldsymbol{\hat\theta}_0),g(\boldsymbol{\hat\theta}_1)\) — typically independent simulations

Statistical model

Economic model

Status quo

New drug

Decision analysis

Status quo
Benefits Costs
741 670382.1
699 871273.3
... ...
726 425822.2
716.2 790381.2

New drug
Benefits Costs
732 1131978
664 1325654
... ...
811 766411.4
774.5 1066849.8

4. Uncertainty analysis

Uncertainty induced by \(g(\boldsymbol{\hat\theta}_0),g(\boldsymbol{\hat\theta}_1)\) — typically independent simulations

Statistical model

Economic model

Status quo

New drug

Decision analysis

Status quo
Benefits Costs
741 670382.1
699 871273.3
... ...
726 425822.2
716.2 790381.2

New drug
Benefits Costs
732 1131978
664 1325654
... ...
811 766411.4
774.5 1066849.8

4. Uncertainty analysis

Uncertainty induced by \(g(\boldsymbol{\hat\theta}_0),g(\boldsymbol{\hat\theta}_1)\) — typically independent simulations

Statistical model

Economic model

Status quo

New drug

Decision analysis

Status quo
Benefits Costs
741 670382.1
699 871273.3
... ...
726 425822.2
716.2 790381.2

New drug
Benefits Costs
732 1131978
664 1325654
... ...
811 766411.4
774.5 1066849.8

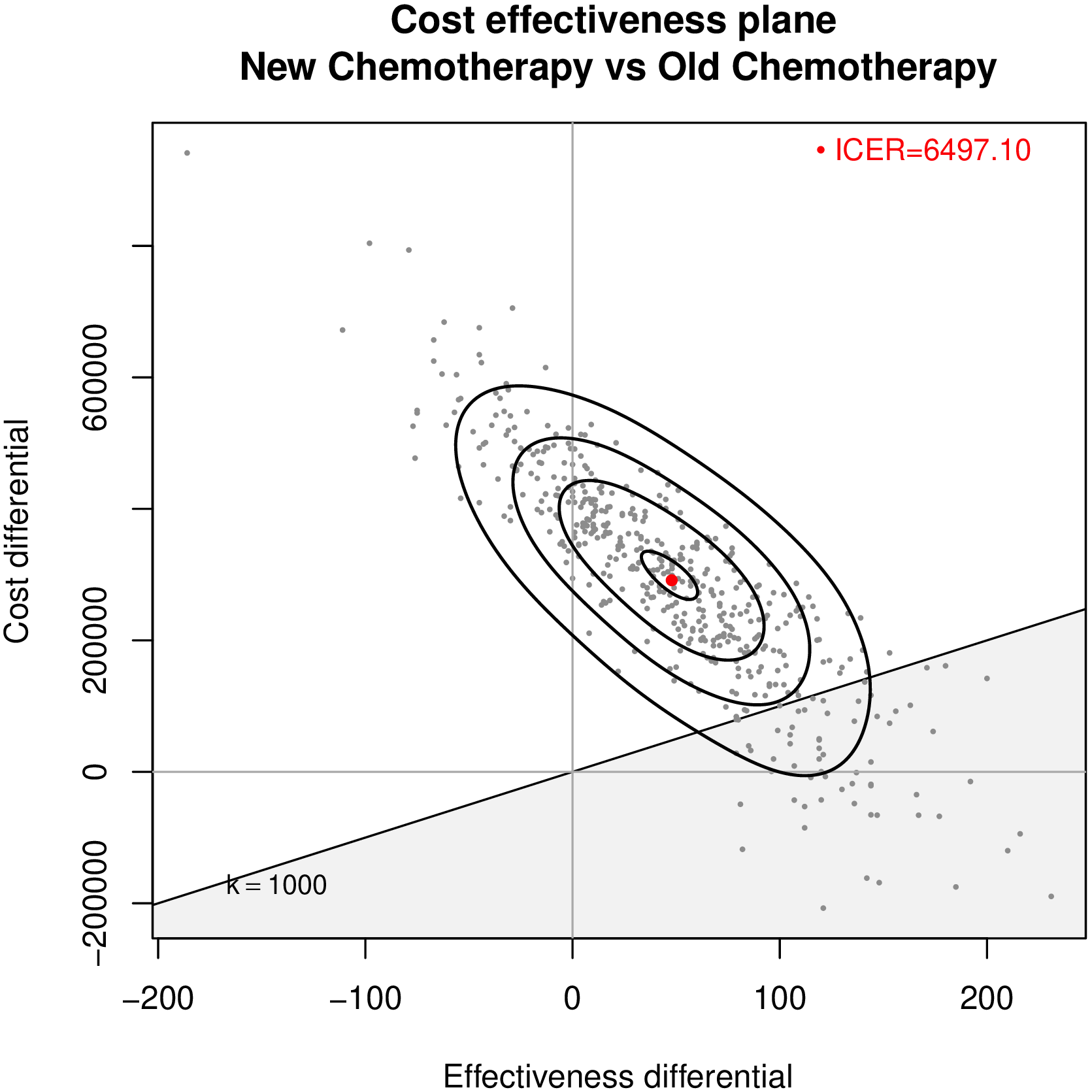
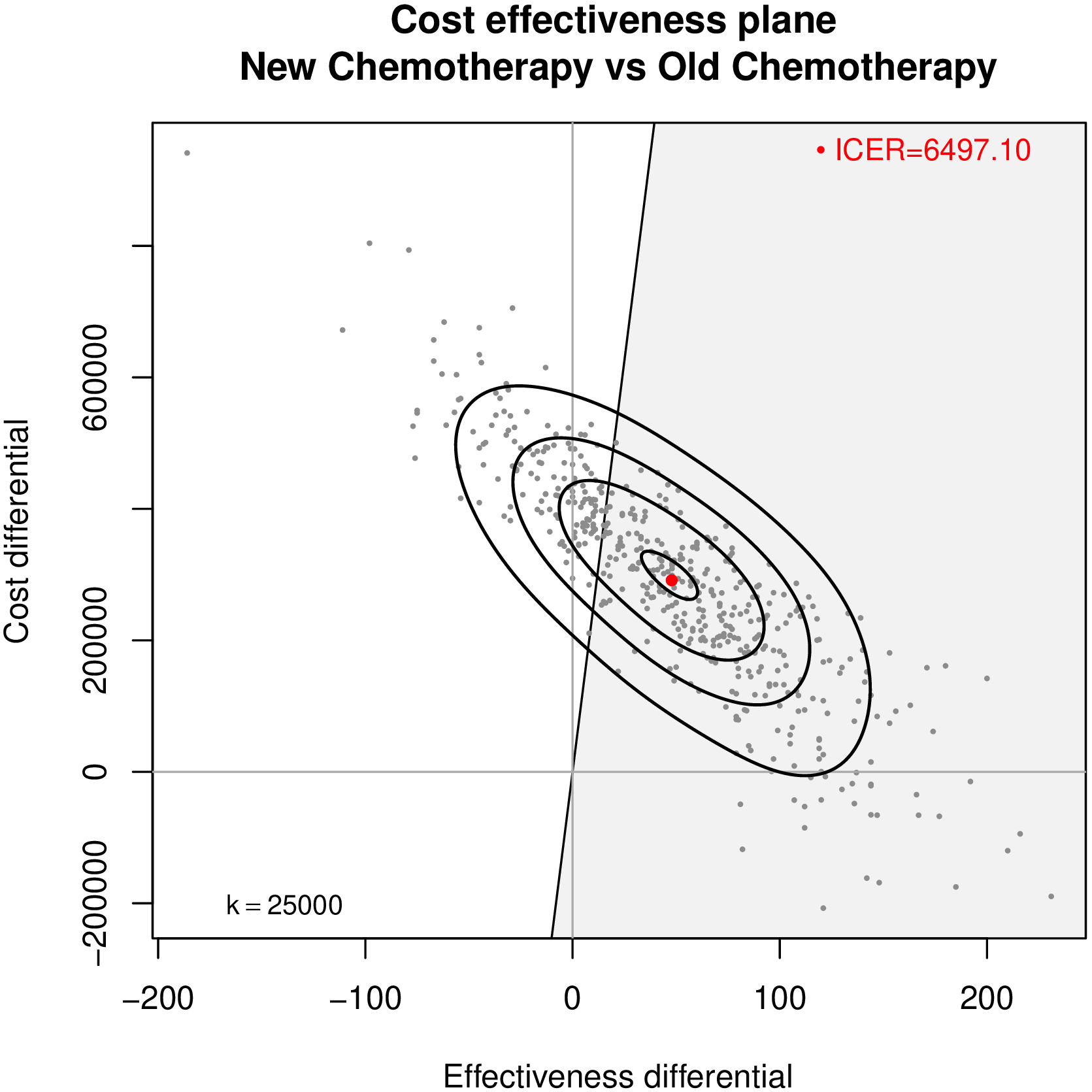
\[ \begin{align} \class{myblue}{\style{font-family:inherit;}{\text{ICER}}} & \class{myblue}{=} \frac{\class{myblue}{\style{font-family:inherit;}{\text{276468.6}}}}{\class{myblue}{\style{font-family:inherit;}{\text{58.3}}}}\\ & \class{myblue}{= \style{font-family:inherit;}{\text{6497.1}}} \end{align} \]

4. Uncertainty analysis*

\[\class{myblue}{\Delta_e=}\class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\theta}_1]}}_{\class{red}{\mu_{e1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\theta}_0]}}_{\class{red}{\mu_{e0}}}}\]

\[\class{myblue}{\Delta_c=}\class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\theta}_1]}}_{\class{red}{\mu_{c1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\theta}_0]}}_{\class{red}{\mu_{c0}}}}\]

*Induced by \(\class{myblue}{g(\boldsymbol{\hat\theta}_0),g(\boldsymbol{\hat\theta}_1)}\)

What’s wrong with this?…

  • Potential correlation between costs & clinical benefits (Individual level + Aggregated level Data)
    • Strong positive correlation – effective treatments are innovative and result from intensive and lengthy research \(\Rightarrow\) are associated with higher unit costs
    • Negative correlation - more effective treatments may reduce total care pathway costs e.g. by reducing hospitalisations, side effects, etc.
    • Because of the way in which standard models are set up, bootstrapping generally only approximates the underlying level of correlation – (MCMC does a better job!)
  • Joint/marginal normality not realistic (Mainly ILD)
    • Costs usually skewed and benefits may be bounded in \([0; 1]\)
    • Can use transformation (e.g. logs) – but care is needed when back transforming to the natural scale
    • Should use more suitable models (e.g. Beta, Gamma or log-Normal) – (generally easier under a Bayesian framework)
    • Particularly relevant in presence of partially observed data – more on this later!
  • Particularly as the focus is on decision-making (rather than just inference), we need to use all available evidence to fully characterise current uncertainty on the model parameters and outcomes (Mainly ALD)
    • A Bayesian approach is helpful in combining different sources of information
    • (Propagating uncertainty is a fundamentally Bayesian operation!)

To be or not to be?… (A Bayesian)

In HTA

Frequentist (“standard”)

Bayesian

4. Uncertainty analysis

Uncertainty induced by \(\class{myblue}{p(\boldsymbol\theta\mid \txt{data})}\) — uses the joint posterior of all the parameters!

Statistical model

Economic model

Status quo

New drug

Decision analysis

Status quo
Benefits Costs
741 670382.1
699 871273.3
... ...
726 425822.2
716.2 790381.2

New drug
Benefits Costs
732 1131978
664 1325654
... ...
811 766411.4
774.5 1066849.8

\[ \begin{align} \class{myblue}{\style{font-family:inherit;}{\text{ICER}}} & \class{myblue}{=} \frac{\class{myblue}{\style{font-family:inherit;}{\text{276468.6}}}}{\class{myblue}{\style{font-family:inherit;}{\text{58.3}}}}\\ & \class{myblue}{= \style{font-family:inherit;}{\text{6497.1}}} \end{align} \]

2./4. Economic model + Uncertainty analysis*

\[\class{myblue}{\Delta_e=}\class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\theta}_1]}}_{\class{red}{\mu_{e1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\theta}_0]}}_{\class{red}{\mu_{e0}}}}\]

\[\class{myblue}{\Delta_c=}\class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\theta}_1]}}_{\class{red}{\mu_{c1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\theta}_0]}}_{\class{red}{\mu_{c0}}}}\]

*Induced by \(\class{myblue}{p(\boldsymbol{\theta} \mid \style{font-family:inherit;}{\text{data}})}\)

3. Decision analysis

\[\class{myblue}{\Delta_e=}\class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\theta}_1]}}_{\class{red}{\mu_{e1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[e \mid \boldsymbol{\theta}_0]}}_{\class{red}{\mu_{e0}}}}\]

\[\class{myblue}{\Delta_c=}\class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\theta}_1]}}_{\class{red}{\mu_{c1}}}} \class{myblue}{-} \class{red}{\underbrace{\class{myblue}{\E[c \mid \boldsymbol{\theta}_0]}}_{\class{red}{\mu_{c0}}}}\]

Decision-theoretic approach to HTA

  • Analytic framework for decision-making in the face of uncertainty

  • Considers a set of prescriptive axioms to ensure rationality in decision-making

  • Identifies the best course of action given:

    • Model specification
    • Current evidence

Process of rational decision-making

  1. Describe uncertainty on all unknown quantities by means of a (possibly subjective) probability distribution \(\class{myblue}{p(\boldsymbol\omega) = p(e, c \mid \boldsymbol\theta)p(\boldsymbol\theta)}\)

  2. For each intervention \(t\), outcomes \(o = (e, c)\) are valued by means of a pre-specified measure of utility \(\class{myblue}{u(e, c; t)}\)

  3. Select as the most “cost-effective” the intervention that is associated with the maximum expected utility \(\class{myblue}{\mathcal{U}^t = \E_\boldsymbol\omega [u(e, c; t)]}\)

  • Typical utility function in HTA: Monetary Net Benefit \(\class{myblue}{u(e, c; t) = nb_t = ke_t − c_t}\)
    • \(k\) is the “willingness to pay”, i.e. the .red[cost per extra unit of effectiveness gained]
    • Fixed, linear form, which simplifies computations
    • Assumes decision-maker is risk neutral. Not necessarily true!

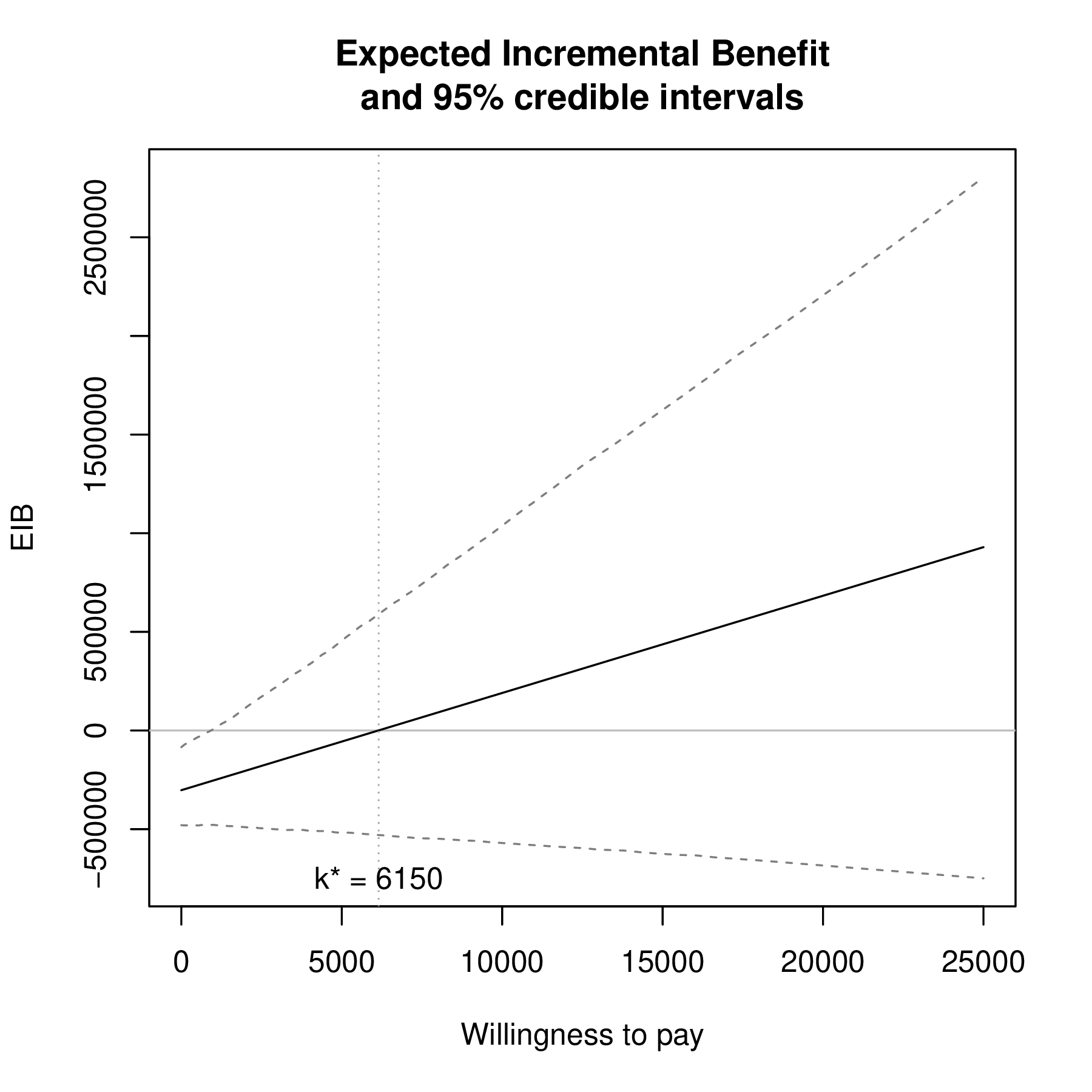
Expected Incremental Benefit

  • Under the MNB, the expected utility is

\[\begin{align} \class{myblue}{\mathcal{U}^t = \mathcal{NB}_t} & \class{myblue}{= \E_{\class{blue}{\boldsymbol\omega}}[u(e,c;t)]} \\ & \class{myblue}{= k\E_{\class{blue}{\boldsymbol\omega}}[e_t] - \E_{\class{blue}{\boldsymbol\omega}}[c_t]} \\ & \class{myblue}{= k\E_{\class{red}{\boldsymbol\theta}}[e\mid \boldsymbol\theta_t] - \E_{\class{red}{\boldsymbol\theta}}[c\mid \boldsymbol\theta_t] = k\E[\mu_{et}] - \E[\mu_{ct}]} \end{align}\]

The expectation is taken with respect to \(p(\boldsymbol\omega)\) so \(\mathcal{NB}_t\) is a pure number!

  • Assuming we are considering only two interventions \(t=(0,1)\), decision-making can be effected by looking at the Expected Incremental Benefit

\[\begin{align} \class{myblue}{\style{font-family:inherit;}{\text{EIB}}} & \class{myblue}{= \mathcal{NB}_1-\mathcal{NB}_0} \\ & \class{myblue}{= \left(k\E[\mu_{e1}]-\E[\mu_{c1}]\right) - \left(k\E[\mu_{e0}]-\E[\mu_{c0}]\right)} \\ & \class{myblue}{= k\E[\Delta_e] - \E[\Delta_c]} \end{align}\]

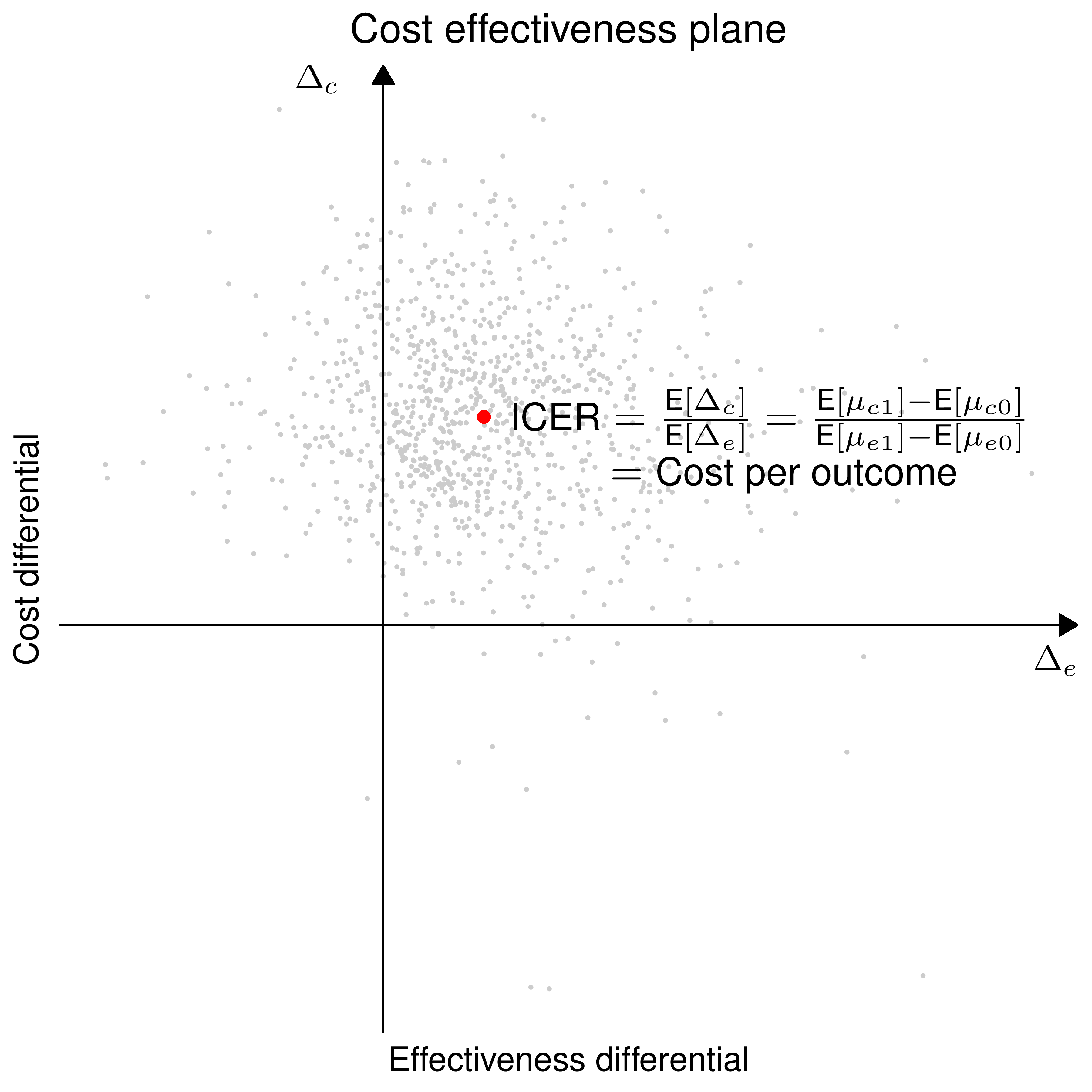
  • The reference treatment \(t=1\) is more cost-effective than the comparator \(t=0\) if \[\begin{equation} \class{myblue}{\style{font-family:inherit;}{\text{EIB}}>0 \Rightarrow k>(<)\frac{\E[\Delta_c]}{\E[\Delta_e]} = \style{font-family:inherit;}{\text{ICER}} \quad \style{font-family:inherit;}{\text{ if }} \E[\Delta_e]>(<)0} \end{equation}\]

ICER vs EIB

ICER vs EIB

Summarising PSA

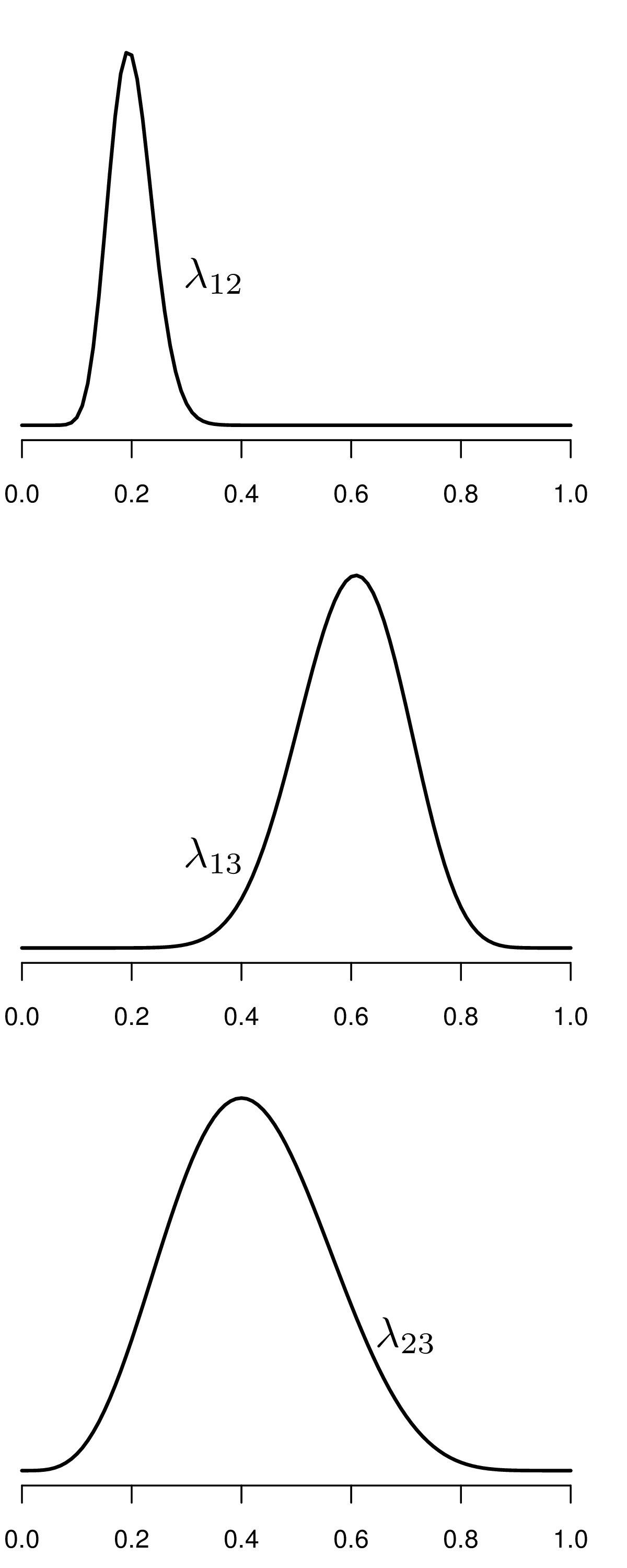
Parameter simulations
Expected utility
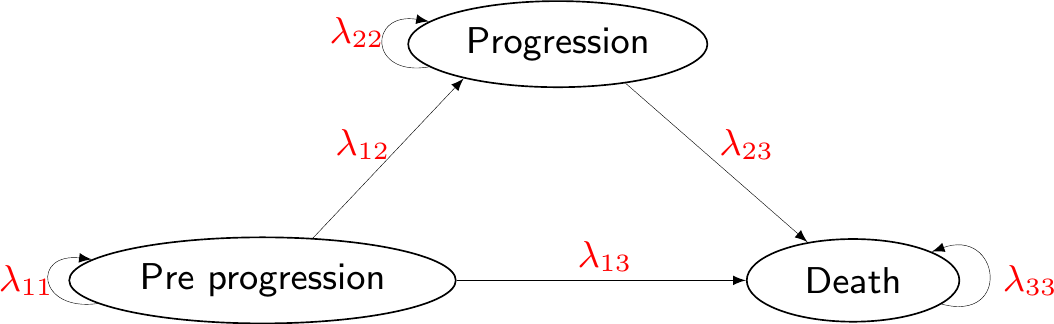
Iteration \(\lambda_1\) \(\lambda_2\) \(\lambda_3\) \(\ldots\) \(\nb_0(\boldsymbol\theta)\) \(\nb_1(\boldsymbol\theta)\) \(\ib(\boldsymbol\theta)\)
1 0.585 0.3814 0.4194 \(\ldots\) 77480 67795 -9685
2 0.515 0.0166 0.0768 \(\ldots\) 87165 106535 19370
3 0.611 0.1373 0.0592 \(\ldots\) 58110 38740 -19370
4 0.195 0.7282 0.7314 \(\ldots\) 77480 87165 9685
\(\ldots\) \(\ldots\) \(\ldots\) \(\ldots\) \(\ldots\) \(\ldots\) \(\ldots\) \(\ldots\)
1000 0.0305 0.204 0.558 \(\ldots\) 48425 87165 38740
Average \(\mathcal{NB}_0=\)72365.35 \(\mathcal{NB}_1=\)77403.49 \(\eib=\)5038.14

  • \(\color{blue}\nb_t(\boldsymbol\theta)=k\mu_{et}-\mu_{ct}\) is the “known distribution” utility

  • \(\color{blue}\ib(\boldsymbol\theta)=\nb_1(\boldsymbol\theta)-\nb_0(\boldsymbol\theta)\) is the incremental benefit (as a function of \(\boldsymbol\theta\))

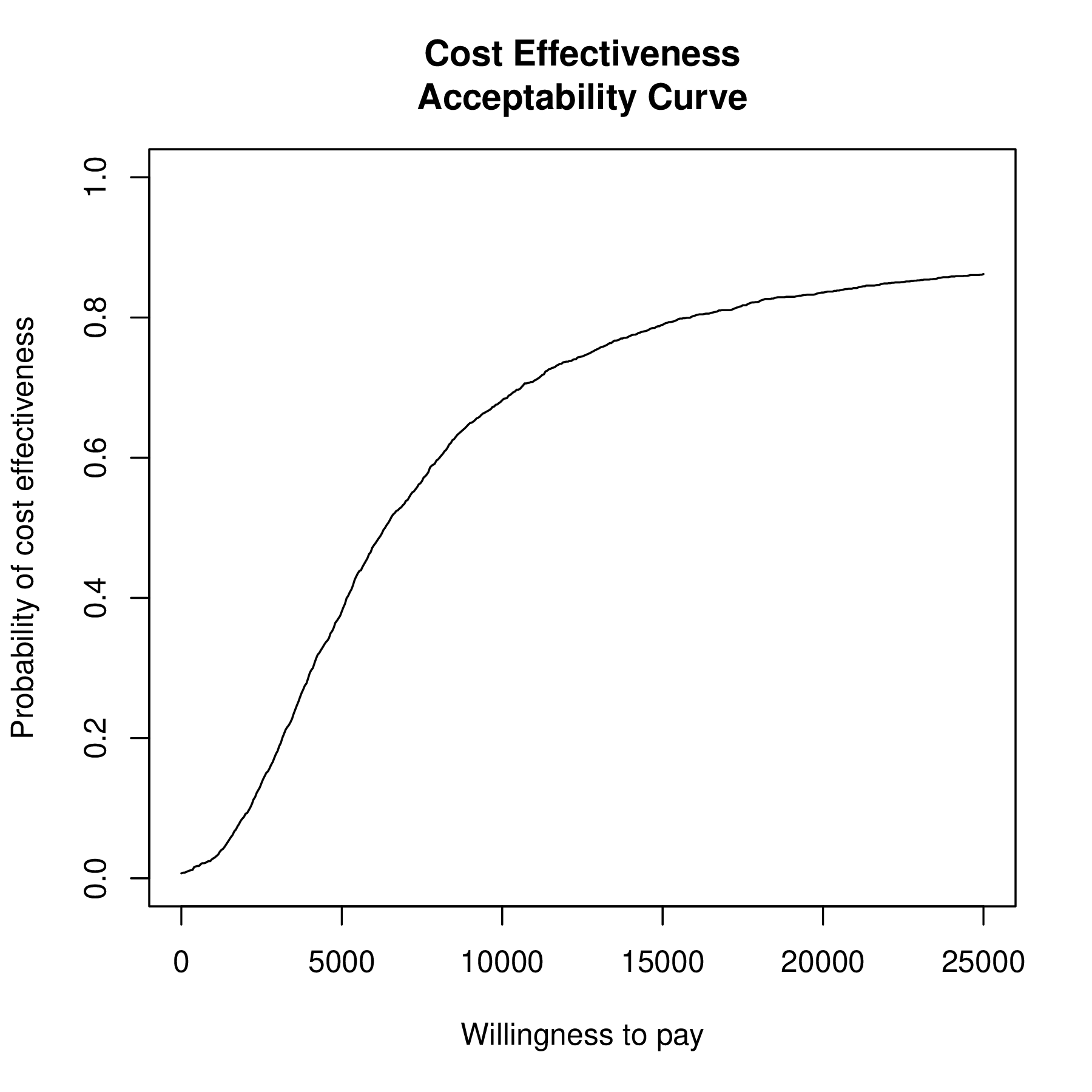
  • Can summarise uncertainty in the decision-making process using the cost-effectiveness acceptability curve

\[\color{blue}\ceac=\Pr(\ib(\boldsymbol\theta)\mid \style{font-family:inherit;}{\text{data}})>0\]

  • Upon varying \(k\), this is the probability that the optimal decision would not be reversed by reducing uncertainty

CE plane vs CEAC

CE plane vs CEAC

1. Intro HTA 2. Bayesian computation 3. ILD 4. ALD 5. NMA   © Gianluca Baio (UCL)   |             |   Bayesian models in HTA   |   VIBASS7 2024   |   10 - 11 July 2024   |