A Bayesian hierarchical framework to evaluate policy effects through quasi-experimental designs
Gianluca Baio
Department of Statistical Science | University College London
https://gianluca.statistica.it
https://egon.stats.ucl.ac.uk/research/statistics-health-economics
https://github.com/giabaio https://github.com/StatisticsHealthEconomics
@gianlubaio@mas.to @gianlubaio
New challenges in the estimation of the impact of policies
XLIII Jornadas de Economia de la Salud, San Cristóbal de la Laguna, Tenerife, Spain
27 June 2024
Check out our departmental podcast “Random Talks” on Soundcloud!
Follow our departmental social media accounts + magazine “Sample Space”
Epitome
Epitome
Examples
- Hostile environment (most of this talk)
- Universal credit (more on this later…)
- Suicides
- Speed limits (20mph zones across large sections of many UK cities)
- …
Contextual/policy background
The Windrush generation
- After the Second World War, the UK faced severe labour shortages. To make up for this they encouraged people from British Colonies to move to the UK, with the promise of jobs, a better standard of living, and British Citizenship
- Between 1948 and 1970, nearly half a million people moved from the Caribbean to Britain. These individuals became known as the Windrush Generation, after the ship which carried some of the first migrants
- The Immigration Act of 1971 meant that only commonwealth citizens who arrived before 1971 were allowed the right to stay in the UK
- However, in 2010 the British Home Office destroyed all migration records from the 1950s and 1960s
- This meant that many people who came to Britain as part of the Windrush Generation, and many of their children, no longer had evidence of their British Citizenship
Hostile environment
- The UK government (under pressure from nationalist/populist parties pushing for brexit), started a series of immigration reforms, collectively known as the hostile environment policy, in 2012
- These policies deliberately aimed to make life difficult for migrants and operated on a “deport first, ask questions later” basis
“… The aim is to create, here in Britain, a hostile environment… We can deport first and hear appeals later…”
Theresa May,
UK Home Secretary (May 2010 — July 2016)
UK Prime Minister (July 2016 — July 2019)
Hostile environment
- This led to British Citizens whose documentation had been destroyed by the home office being unlawfully deported to countries they no longer had any connection with
- It also played into a wider narrative, fuelled by political parties such as UKIP and, in part, the ruling Conservatives — strongly anti-EU and anti-immigration
Immigration Act (2014)
- Requires migration status checks to be carried out before:
- Opening a bank account
- Renting accommodation
- Being offered employment
- Receiving health treatment
- Reporting a crime
- Going to school
- Obtaining a drivers’ license
- These check exacerbated systematic racism
- Often only applied to people who “did not seem British”
- They also meant that people who no longer had evidence of their British Citizenship, through no fault of their own, were often too scared to access essential services, through fear of being deported
The Windrush scandal
In 2017 the “Windrush scandal” hit the mainstream media headlines and cost her job to the new Home Secretary, Amber Rudd, but not to the one who actually enacted the policy…
Modelling & analysis
Data
We use data from The UK Household Longitudinal Survey (“Understanding Society”)
Participants
- Age 16+, responded at least once to mental health questionnaire
Timing
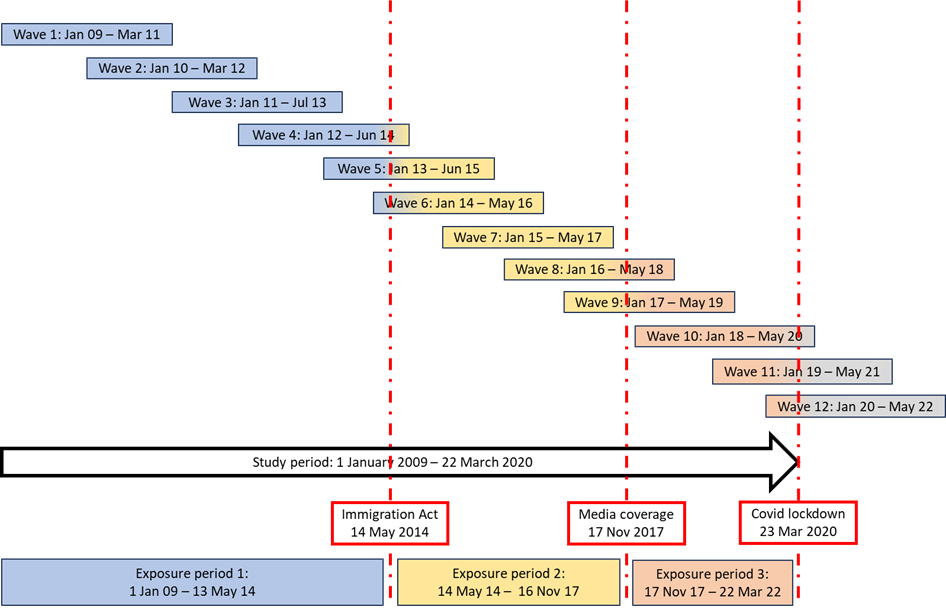
- 12x 24 month “waves”, January 2009 to March 2020
- Avoid “Covid” confounding…
Outcome & exposure
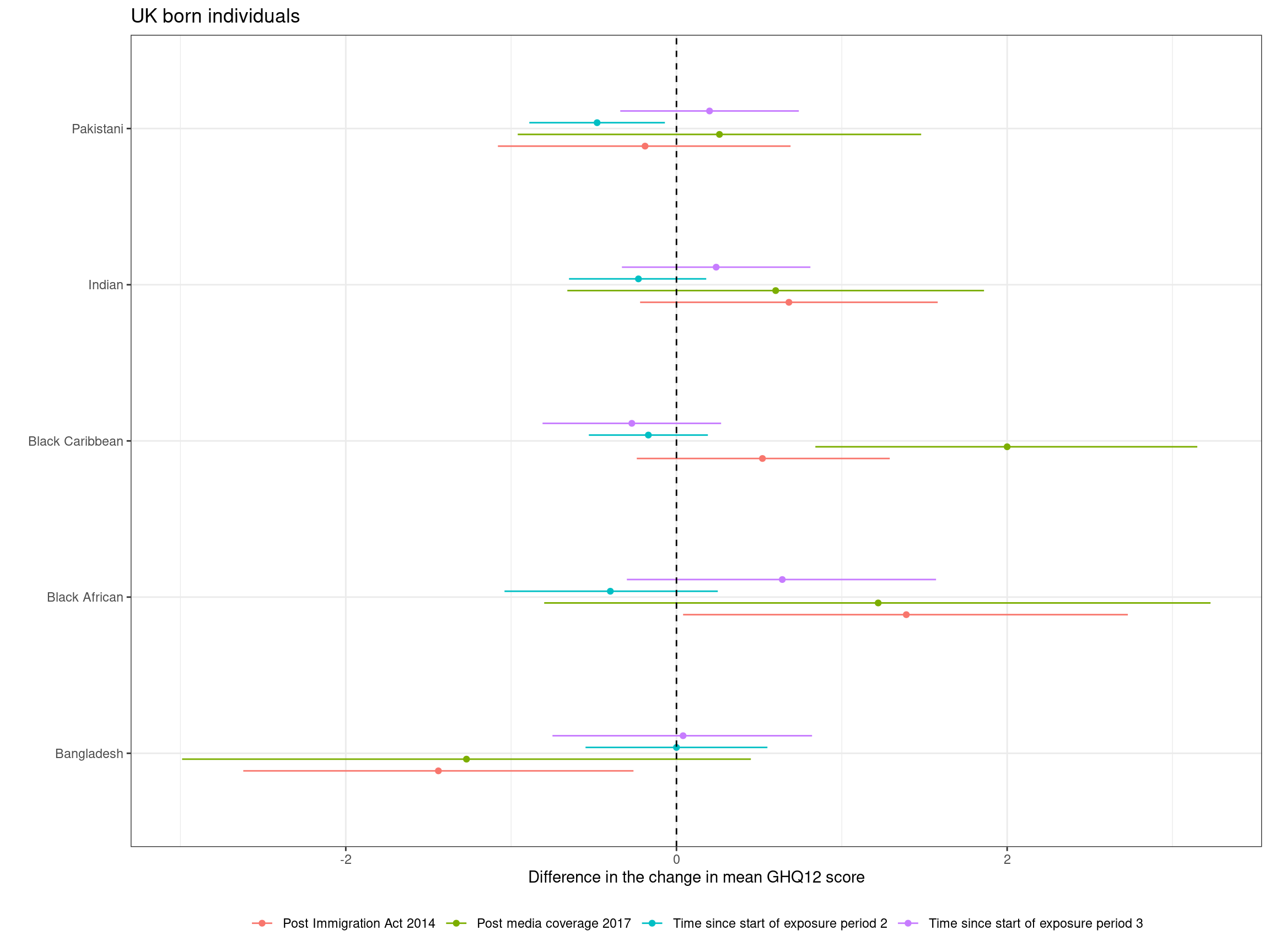
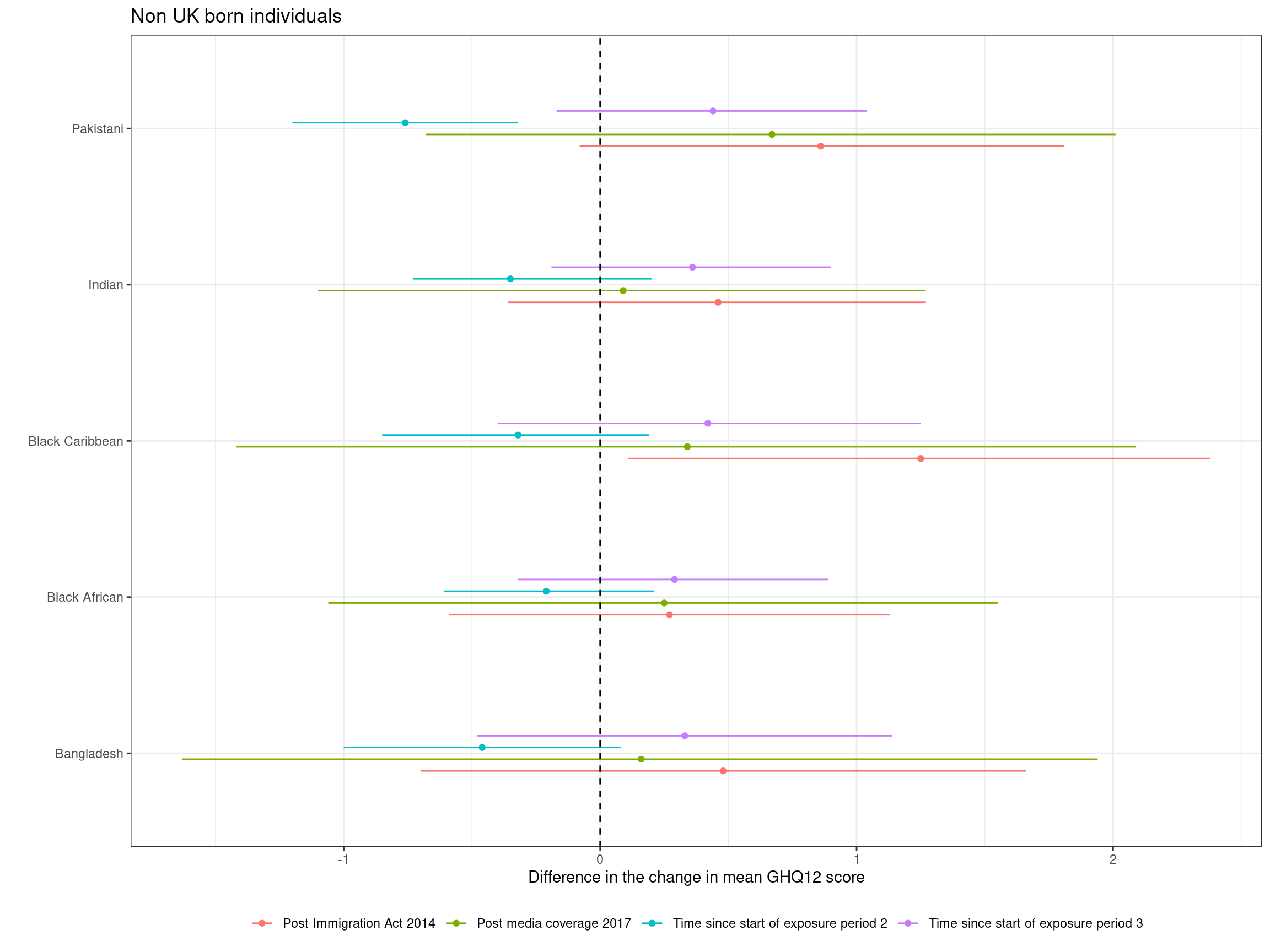
- Outcome: Mental ill health, GHQ-12 — higher scores indicating more severe impairment
- Exposures:
- Immigration Act 2014
- Windrush media coverage 2017
- Exposed ethnicities: Black African, Black Caribbean, Indian, Pakistani, Bangladeshi vs White
- Main confounders: age, sex, urban/rural, IMD, children, UK born, education, working condition
Study design
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
\[ g\left(\E[Y_{it}]\right) = g(\mu_{it}) \color{white}{= \alpha_0 + \alpha_1 w_i + \sum_{k=1}^K \beta_k X_{itk} + \phi_{0}t + \phi_{1}t w_i + \delta_0 z_{t} + \delta_1 w_i z_t + \gamma_i + \lambda_t} \,[+\ldots] \]
- \(g(\cdot)\) is a suitable link function
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
\[ g\left(\E[Y_{it}]\right) = g(\mu_{it}) = \alpha_0 + \alpha_1 w_i \color{white}{+ \sum_{k=1}^K \beta_k X_{itk} + \phi_{0}t + \phi_{1}t w_i + \delta_0 z_{t} + \delta_1 w_i z_t + \gamma_i + \lambda_t} [+\ldots] \]
- \(g(\cdot)\) is a suitable link function
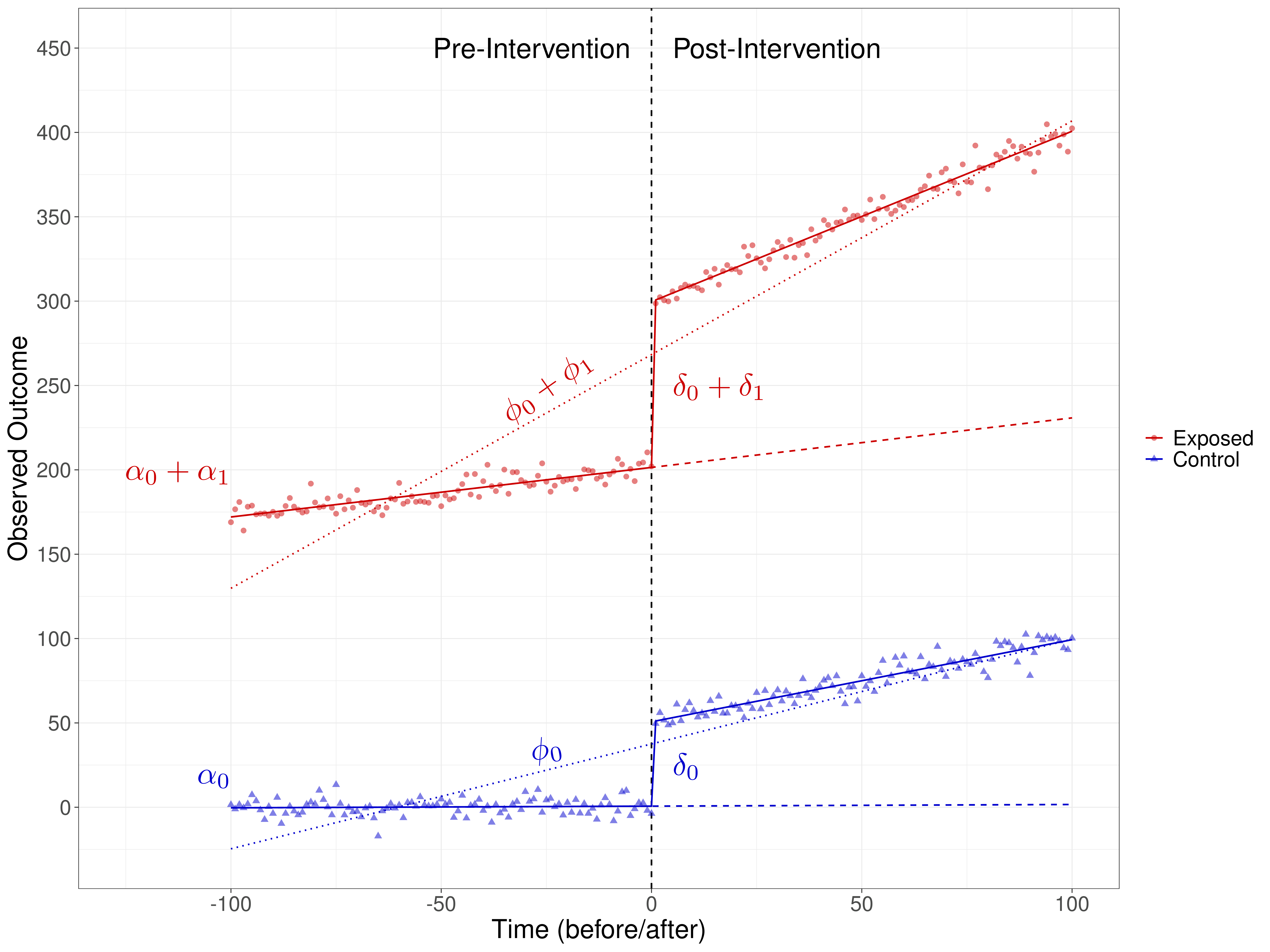
- \(\alpha_0\) and \((\alpha_0+\alpha_1)\) are the the baseline intercept in the controls and exposed, respectively
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
\[ g\left(\E[Y_{it}]\right) = g(\mu_{it}) = \alpha_0 + \alpha_1 w_i + \sum_{k=1}^K \beta_k X_{itk} \color{white}{+ \phi_{0}t + \phi_{1}t w_i + \delta_0 z_{t} + \delta_1 w_i z_t + \gamma_i + \lambda_t} [+\ldots] \]
- \(g(\cdot)\) is a suitable link function
- \(\alpha_0\) and \((\alpha_0+\alpha_1)\) are the the baseline intercept in the controls and exposed, respectively
- \(\bm{\beta}=(\beta_1,\ldots,\beta_K)\) quantifies the effect of the confounders \(\bm{X}_{it}\)
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
\[ g\left(\E[Y_{it}]\right) = g(\mu_{it}) = \alpha_0 + \alpha_1 w_i + \sum_{k=1}^K \beta_k X_{itk} + \phi_{0}t + \phi_{1}t w_i \color{white}{+ \delta_0 z_{t} + \delta_1 w_i z_t + \gamma_i + \lambda_t} [+\ldots] \]
- \(g(\cdot)\) is a suitable link function
- \(\alpha_0\) and \((\alpha_0+\alpha_1)\) are the the baseline intercept in the controls and exposed, respectively
- \(\bm{\beta}=(\beta_1,\ldots,\beta_K)\) quantifies the effect of the confounders \(\bm{X}_{it}\)
- \(\phi_{0}\) and \((\phi_{0}+\phi_{1})\) are the linear time trend in the controls and exposed, respectively
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
\[ g\left(\E[Y_{it}]\right) = g(\mu_{it}) = \alpha_0 + \alpha_1 w_i + \sum_{k=1}^K \beta_k X_{itk} + \phi_{0}t + \phi_{1}t w_i + \delta_0 z_{t} + \delta_1 w_i z_t \color{white}{+ \gamma_i + \lambda_t} [+\ldots] \]
- \(g(\cdot)\) is a suitable link function
- \(\alpha_0\) and \((\alpha_0+\alpha_1)\) are the the baseline intercept in the controls and exposed, respectively
- \(\bm{\beta}=(\beta_1,\ldots,\beta_K)\) quantifies the effect of the confounders \(\bm{X}_{it}\)
- \(\phi_{0}\) and \((\phi_{0}+\phi_{1})\) are the linear time trend in the controls and exposed, respectively
- \(\delta_0\) and \((\delta_0+\delta_1)\) model the change in the outcome pre-post intervention in the controls and the exposed, respectively
Interrupted time series
General model structure
- \(y_{it}\) is the outcome for unit \(i=1\ldots,I\) and time \(t=1,\ldots T\geq 2\)
- \(\bm{X}_{it}=(X_{it1},\ldots,X_{itK})\) is a vector of \(K\) covariates (confounders)
- \(z_{t}=1\) if the intervention is being applied at time \(t\) and 0 otherwise
- \(w_{i}=1\) if unit \(i\) is exposed and 0 if it is a control
\[ g\left(\E[Y_{it}]\right) = g(\mu_{it}) = \alpha_0 + \alpha_1 w_i + \sum_{k=1}^K \beta_k X_{itk} + \phi_{0}t + \phi_{1}t w_i + \delta_0 z_{t} + \delta_1 w_i z_t + \gamma_i + \lambda_t \,[+\ldots] \]
- \(g(\cdot)\) is a suitable link function
- \(\alpha_0\) and \((\alpha_0+\alpha_1)\) are the the baseline intercept in the controls and exposed, respectively
- \(\bm{\beta}=(\beta_1,\ldots,\beta_K)\) quantifies the effect of the confounders \(\bm{X}_{it}\)
- \(\phi_{0}\) and \((\phi_{0}+\phi_{1})\) are the linear time trend in the controls and exposed, respectively
- \(\delta_0\) and \((\delta_0+\delta_1)\) model the change in the outcome pre-post intervention in the controls and the exposed, respectively
- \(\bm{\gamma}=(\gamma_1,\ldots,\gamma_I)\) are a set of unit-specific random effects to model dependencies across the units
- \(\bm\lambda=(\lambda_1,\ldots,\lambda_T)\) quantifies the time trends for the overall period, modelled using autoregressive structures, which will allow to increase the model flexibility
- \([+\ldots]\) (optional) additional structured effect (e.g. to model spatial correlation)
Interrupted time series
Typical analysis
To be or not to be (a Bayesian)?…
- Can include relatively vague information in the priors, which can still help regularise the inference
- Avoid inconsistent estimates because of small numbers/separation
- Use Penalised Complexity (PC) priors
- Direct characterisation of full uncertainty in all model parameters
- Can then rescale (e.g. from regression coefficients to original scores etc) and still obtain samples from the full posterior distributions
- Particularly helpful for generalised linear models
NB: The answer is always “Yes”… 😉
Results
Hostile environment
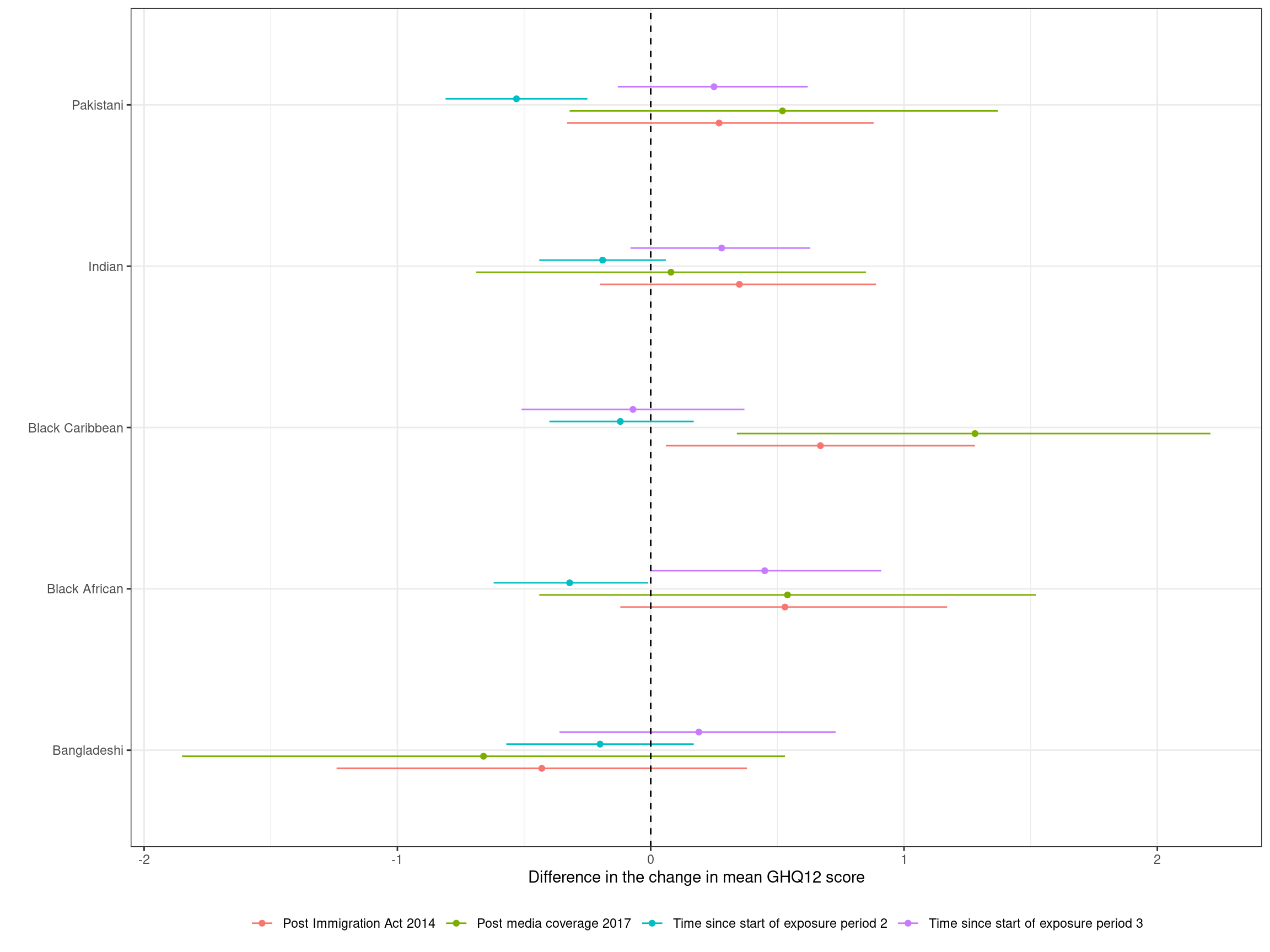
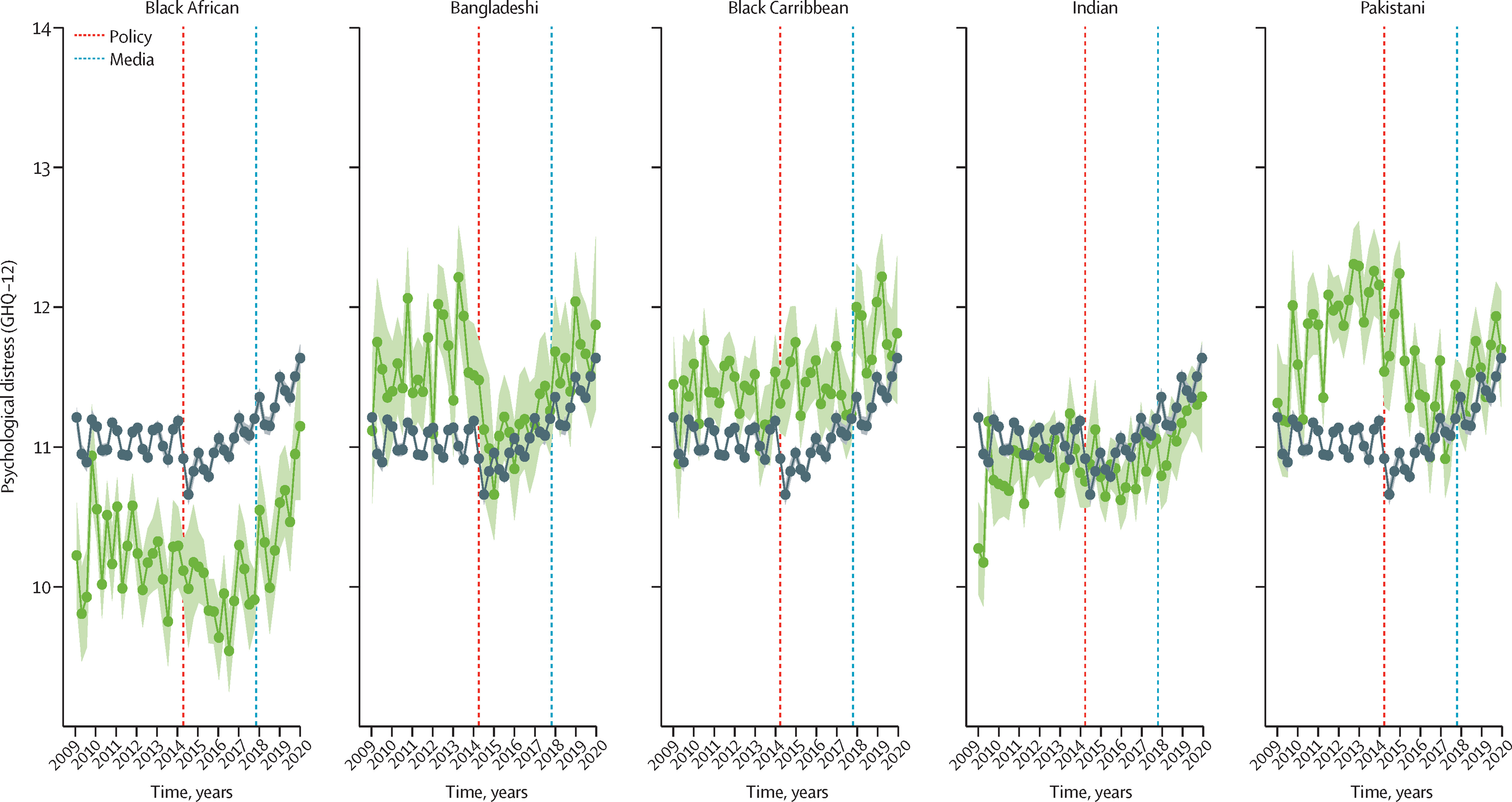
Results
Hostile environment
Results
Hostile environment
Results — subgroup analysis
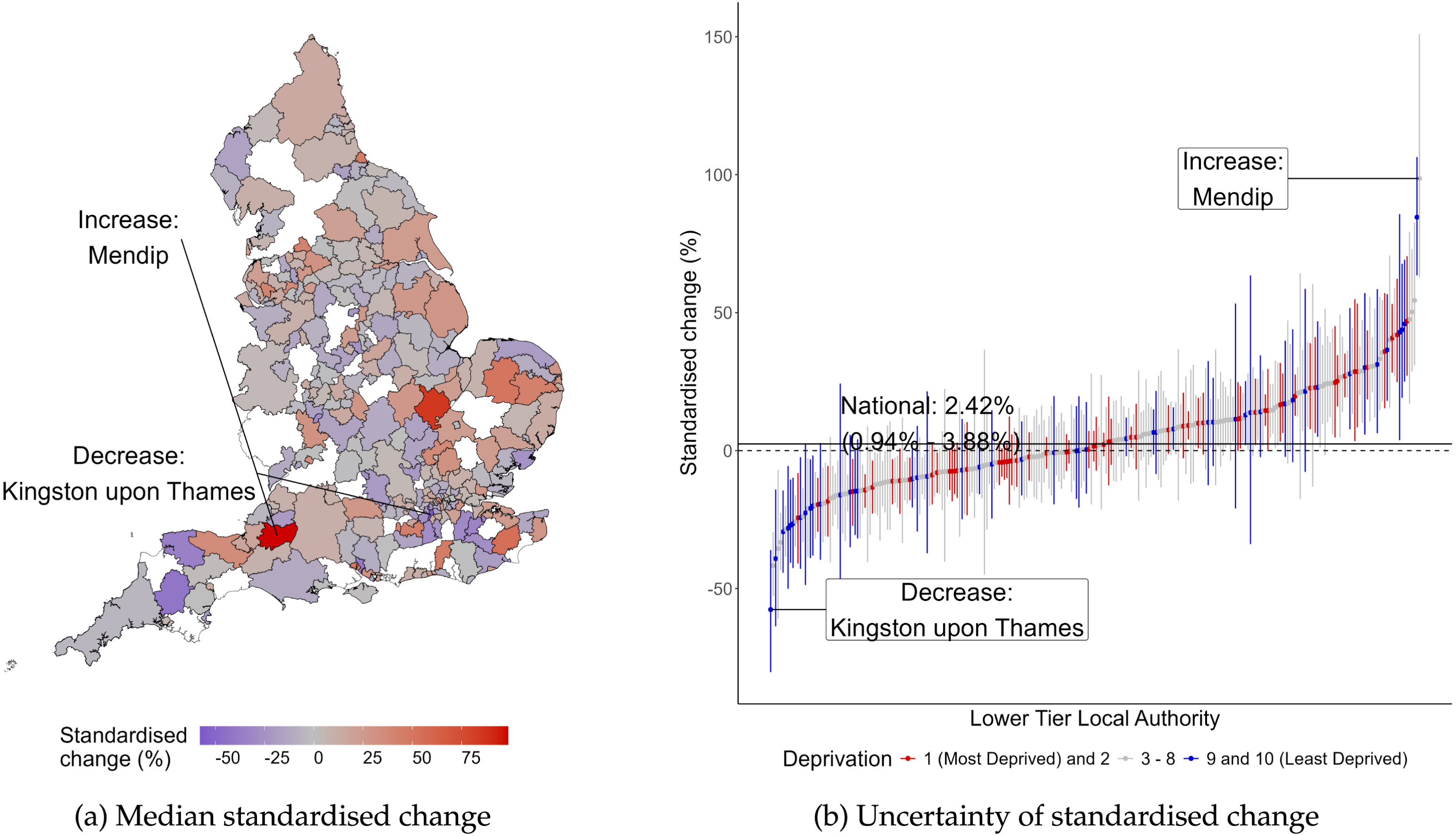
Universal credit
Results — spatial variation
© Gianluca Baio (UCL) | | Bayesian ITS et al | AES 2024 | 27 Jun 2024 | Slides available at https://giabaio.github.io/aes-2024